IdentifiantMot de passe
Mot de passe oublié ?Je m'inscris ! (gratuit)

Octave numérique

L'espace de l'octave majeure

L'octave majeure compose les sept notes tempérées, en définissant la gamme naturelle de Do. Le tempérament diatonique a le sens de l'intervalle, et naturellement lié au mode chromatique majeur.

Tout en concervant son aspect original, la gamme a maintenant une valeur ajoutée via le nombre. Ce dernier, étant le tempérament unitaire, tel pour une unité "1" cumulée jusqu'au "12" chromatique.

Disposition d'une octave diatonique dans l'espace chromatique, où les notes sont "vraies", et les intervalles sont "faux". L'information donnée par la répartition des charges, elles est localisée supérieurement par rapport aux réalités de l'octave.

Comme il est question de tempéramant unitaire, il faut savoir que certaines valeurs peuvent être modifiées. Ce développé réuni un chromatisme d'octave, et une gamme naturelle. Modifier à l'aide de l'unité chromatique ou bien gammique, devrait pouvoir se faire...
Signaler un problème
Avatar de
https://www.developpez.com
Le 28/10/2018 à 14:01
Composition avancée
À l’échelle zéro, il y a l’octave mesurée en douze parts égales, et les premiers nombres.

En manière élémentaire, les nombres représentent des quantités. Chaque nombre peut être exprimé en poids, ainsi le poids du nombre est utile à la pesée d’une octave. L’octave assemble plusieurs nombres, elle mesure douze unités numériques, en apportant un composé (vrai/faux).

Par définition, l’octave a deux états complémentaires. Elle se compose principalement d’éléments réels, ou de vraies notes relatives. Elle a sept unités tempérées, et pour le cas relatives aux nombres. Elle occupe l’espace de douze unités chromatiques, allant de 1 à 12 avec seulement 7 notes. Ces dernières produisent les intervalles, là où il n’y a pas de note vraie. Là où commencent les fausses notes, celles qui sont dans l’ombre.

Une trame se crée à l’aide de ce clair/obscur, à l’aide du poids des nombres. Le poids des notes vraies est inférieur à celui des fausses, d’où un intervalle plus important en poids ? Le calcul de l’intervalle est porté sur le cumul des poids faibles, donc chaque élément intermédiaire a une entité. Il y a une autre façon de mesurer l’intervalle, en soustrayant le point réel faible de son point fort. Ce qui donne un nombre d’unités comme différence de taille, sans tenir compte des teneurs liées.

Comparer l’intervalle réel et figuré
Pour deux réalités :
1. Supérieur = 7
2. Inférieur = 3
Calcul de l’intervalle réel
Soustraction de l’inférieur au supérieur (7-3=4)
Opération du sens figuré
Accumulation vraie de l’inférieur et du supérieur (7+3=10)
Accumulation fausse entre l’inférieur et le supérieur (4+5+6=15)

Il n’est pas vraiment compliqué de calculer l’intervalle, de mesurer l’espace qu’il y a entre voisinages. Ce qui est magique, c’est que l’octave a des éléments concrétisés par les nombres, facilitant ainsi l’opération sur l’absence de l’intervalle. À l’échelle de l’octave majeure, la structure chromatique inclut la tonalité harmonique, qui a des notes vraies influencées par les intervalles.
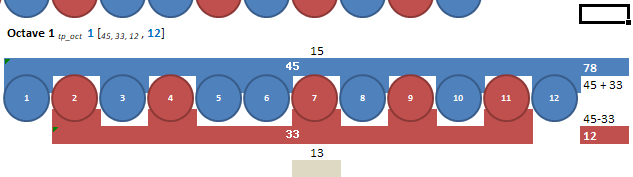
Octave 1 tp_oct 1 [45, 33, 12, 12]
Avatar de
https://www.developpez.com
Le 02/11/2018 à 14:34
Si des charges vraies et fausses composent les tonalités, et que dans un premier temps diatonique, se développe naturellement la gamme naturelle majeure. Chaque gamme a une portée liée à des charges, à décharge du vrai et de l'intervalle. L'existant est une liste contenant les intervalles diatoniques, et une autre avec les noms oraux ou les appellations. Les intervalles diatoniques sont au nombre de sept éléments, puisque sous-forme de quantités locales. L'avenant a nécessité la transposition d'une liste (7), vers son homologue chromatique (12).

L'en cours se réduit à la sélection via une liste des tonalités relatives, ayant pour option de croiser deux tonalités. À charge & à décharge

Existant:
Les gammes ont une liste formée des intervalles.
Elles nous informent des quantités de demi-tons.
Leurs capacités à sept distinctions d'intervalle.
Les noms des gammes dans une liste des oraux.
Les appellations des tonalités et altérations.
Les sélections de recherche par la tonalité.
L'avenant:
La liste des tonalités compose le traitement.
Appliquée à extraire les gammes recherchées.
D'y discerner les charges diatoniques relatives.
Résolution liée à l'existant par la transposition.
D'une liste(7) à une chromatique(12) = Traitement.
Production des gammes au point du premier nombre.
tyrtamos
Avatar de tyrtamos
Expert éminent https://www.developpez.com
Le 03/11/2018 à 15:04
Bonjour,

En lisant ce fil, je découvre la chance que j'ai de pouvoir prendre du plaisir à écouter de la belle musique sans avoir à comprendre tout ça...
Avatar de
https://www.developpez.com
Le 04/11/2018 à 6:51
Citation Envoyé par tyrtamos Voir le message
Bonjour,

En lisant ce fil, je découvre la chance que j'ai de pouvoir prendre du plaisir à écouter de la belle musique sans avoir à comprendre tout ça...
Il n'est pas faux de dire qu'après ça, le plaisir soit différent. Puis "ça" çà a un sens qui ne se comprend qu'avec un plaisir particulier, celui d'avoir le privilège plaisir de suivre le chemin de l'évolution musicale. D'un, "ça" ne nuit pas au plaisir d'écouter de la bonne musique. De deux, "ça" permet d'avancer dans la compréhension de la musique.

J'imagine qu'une vie sans musique, et plus exactement sans écoute, elle écarte la chance de ce qu'on fait le mieux "son". On entend bien tous ces sons naturels de la vie, on en a besoin pour libérer nos neurones lorsqu'elles sont figées "comme c'est le cas avec ça". Aussi j'ai une astuce, je travaille en écoutant de la musique et c'est d'autant plus possible que je travaille seul. Car entre les logiques qui paraissent moteurs dans l'histoire de "ça", ne sont pas étrangères à la musique qu'elles essaient de produire. L'octave fait partie de la musique, mais pas uniquement. Elle fait une part belle aux autres sciences, en faisant acte d'un fait:

Si elle n'est pas fondamentale, dans le temps elle en est la seconde harmonique

[SPOILER]
Code : Sélectionner tout 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
#!/usr/bin/env python3.7
# -*- coding: utf-8 -*-
#
# Formes numérales des gammes
gammes = [[1, 1, 0, 1, 1, 1, 0], [0, 2, 0, 1, 1, 1, 0], [2, 0, 0, 1, 1, 1, 0],
          [4, 0, 0, 0, 0, 1, 0], [1, 0, 1, 1, 1, 1, 0], [0, 1, 1, 1, 1, 1, 0],
          [1, 0, 3, 0, 0, 1, 0], [1, 2, 1, 0, 0, 1, 0], [2, 2, 0, 0, 0, 1, 0],
          [0, 0, 1, 2, 1, 1, 0], [1, 3, 0, 0, 0, 1, 0], [0, 0, 2, 1, 1, 1, 0],
          [1, 2, 2, 0, 0, 0, 0], [0, 0, 4, 0, 0, 1, 0], [1, 4, 0, 0, 0, 0, 0],
          [1, 0, 0, 2, 1, 1, 0], [0, 1, 0, 2, 1, 1, 0], [1, 1, 3, 0, 0, 0, 0],
          [0, 0, 0, 3, 1, 1, 0], [1, 1, 0, 0, 2, 1, 0], [0, 2, 0, 0, 2, 1, 0],
          [0, 2, 0, 2, 0, 1, 0], [2, 0, 0, 0, 2, 1, 0], [1, 0, 1, 0, 2, 1, 0],
          [1, 0, 1, 2, 0, 1, 0], [1, 1, 1, 2, 0, 0, 0], [2, 0, 0, 3, 0, 0, 0],
          [0, 0, 2, 0, 2, 1, 0], [1, 2, 0, 2, 0, 0, 0], [1, 0, 0, 3, 0, 1, 0],
          [1, 0, 0, 1, 2, 1, 0], [1, 1, 0, 3, 0, 0, 0], [1, 1, 2, 1, 0, 0, 0],
          [0, 1, 0, 0, 3, 1, 0], [0, 0, 1, 0, 3, 1, 0], [0, 0, 0, 1, 3, 1, 0],
          [0, 0, 0, 2, 2, 1, 0], [1, 0, 0, 0, 3, 1, 0], [0, 0, 2, 2, 0, 1, 0],
          [0, 0, 0, 0, 4, 1, 0], [0, 0, 2, 3, 0, 0, 0], [1, 0, 0, 4, 0, 0, 0],
          [0, 0, 0, 5, 0, 0, 0], [1, 1, 0, 1, 0, 2, 0], [1, 1, 0, 1, 2, 0, 0],
          [0, 2, 0, 1, 0, 2, 0], [0, 2, 0, 1, 2, 0, 0], [2, 0, 0, 1, 0, 2, 0],
          [2, 0, 0, 1, 2, 0, 0], [1, 0, 1, 1, 0, 2, 0], [1, 0, 1, 1, 2, 0, 0],
          [1, 1, 0, 0, 1, 2, 0], [1, 1, 0, 0, 3, 0, 0], [1, 1, 0, 2, 1, 0, 0],
          [1, 1, 2, 0, 1, 0, 0], [0, 2, 0, 0, 0, 3, 0], [1, 0, 0, 2, 2, 0, 0],
          [1, 0, 0, 1, 0, 3, 0], [1, 3, 0, 0, 1, 0, 0], [1, 0, 0, 0, 1, 3, 0],
          [0, 0, 0, 3, 0, 2, 0], [0, 0, 2, 1, 2, 0, 0], [1, 0, 0, 0, 0, 4, 0],
          [0, 0, 0, 3, 2, 0, 0], [1, 1, 0, 0, 0, 3, 0], [3, 0, 0, 0, 0, 2, 0]]
# Forme orales des gammes
diaton = ['0', '-2', '+2', '^2', '-3', '-23', '-34x', '+34', '+23x', '-34', 'x3',
          '°3', '+34x', '°34x', '^3', '-4', '-24', '^4', '°4', '-5', '-25', '-25+',
          '+25-', '-35', '-35+', '+45x', '+25x', '°35-', '+35x', '-45+', '-45',
          'x5', 'x45+', '-25°', '-35°', '-45°', '°45-', '°5', '°35+', '*5', '°35x',
          '-45x', '°45x', '-6', '+6', '-26', '-26+', '+26-', '+26', '-36', '-36+',
          '-56', '-56+', '+56', 'x46+', '-26°', '-46+', '-46°', 'x36+', '-56°',
          '°46-', '°36+', '*6', '°46+', '°6', 'x26-']
signes = ['+', 'x', '^', '-', '°', '*']
assist = """Sélection de la gamme: Voir ci-dessus [diaton]
    La gamme a un nom formé de signes altératifs, et de chiffres.
    Le chiffre donne une tonalité allant de 2 à 6 (de Ré à La).
    Le chiffre donne une tonalité allant de 2 à 6 (de Ré à La).
    Si la tonalité de la gamme comporte deux chiffres (46):
        Résultat = [ 'x46+','-46+','-46°','°46-','°46+' ]
        Tonalité = '46'
    Ou bien, on rassemble les tonalités (4) et (6):
        Partiel = [ '-34x',,'°4',,'+6',,'x26-',, ]
        Tonalité = '4 6' (or/and)
    Puis, sélection des tonalités (-4):
        Partiel = [ '-4','-45+','-45',,'-46°' ]
        Tonalité = En cours
    Exemples de tonalités:
        '4+ 6', '2 4', '+2', '45', '3 6+', ..."""
# Composition tonale
tonale = ['3 5', '-2 6+', '+2']

def fiches(a_, b_):
    """Transposition & Cumuls"""
    transe = [1]
    tim = tom = vrai = faux = 0
    for gam in gammes[a_]:  # Transposition Liste
        tim += 1
        if gam == 0 and tim < 12:
            transe.append(1)
        else:
            retour = gam
            while retour > 0:
                transe.append(0)
                tim += 1
                retour -= 1
            if tim < 12:
                transe.append(1)
    for trace in transe:  # Cumul Transposition
        tom += 1
        if trace == 1:
            vrai += tom
        else:
            faux += tom
    print('transe', b_, transe, 'V/F', vrai, faux)

quanta = len(tonale)
partie = []
for ton in range(quanta):
    longer = len(tonale[ton])
    if ' ' not in tonale[ton]:
        gobeur = [tonale[ton]]  # Format Liste Stand
        partie.append(gobeur)
    else:
        double = []  # Format Liste Auto
        compil = ''
        suivre = j = 0
        for i in tonale[ton]:
            if i in signes:
                if tonale[ton][suivre + 1] == ' ':
                    compil = ''
                else:
                    j = i
                    compil = j
                    j = ''
            elif i != ' ' and int(i) < 7:
                if len(compil) != 0:
                    compil += i
                    double.append(compil)
                    suivre += len(compil)
                    compil = ''
                else:  # compil == 0
                    if double and tonale[ton][-1] in signes \
                            and longer - suivre == 1:
                        compil += i
                        compil += tonale[ton][-1]
                        double.append(compil)
                        break
                    elif tonale[ton][suivre] in signes:
                        compil += i
                        compil += tonale[ton][suivre]
                        double.append(compil)
                    else:
                        double.append(i)
            elif i == ' ':
                suivre += 1
        partie.append(double)
print('tonale', tonale)
print('Partie', partie)
print()
for p in partie:
    if len(p) != 1:  # Liste Format Dual
        print('Pp2', p)
        x = 0
        for dia in diaton:
            # (p[0] or p[1]): p[0] couple p[1]
            # (p[0] and p[1]): p[1] couple p[0]
            if (p[0] and p[1]) in dia:
                fiches(x, dia)
            x += 1
    else:
        print('Pp1', p)
        x = 0
        for dia in diaton:  # Liste Format Simple
            if str(p[0]) in dia:
                fiches(x, dia)
            x += 1
[/SPOILER]
Ce code ci-dessus : BaseOctave_1.0 a été amélioré, car on peut demander uniquement le signe de l'altération.)
Avatar de
https://www.developpez.com
Le 07/11/2018 à 13:25
Au commencement, le programme après plusieurs corrections relatives aux traitements des éléments. Ce qui en est vite arrivé à ressembler à du compliqué, toutes ces itérations ont disparues. Par une lecture simple des tonalités :

Repérer le vide pour diviser l'image
Code : Sélectionner tout 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
 
#!/usr/bin/env python3.7 
# -*- coding: utf-8 -*- 
# BaseOctave 2.0 Version Laboratoire 
"""Tracés aux bases des opérations""" 
 
def fiches(a_, b_): 
    """Transposition & Cumuls""" 
    transe = [1] 
    tim = tom = vrai = faux = 0 
    for gam in gammes[a_]:  # Transposition Liste 
        tim += 1 
        if gam == 0 and tim < 12: 
            transe.append(1) 
        else: 
            retour = gam 
            while retour > 0: 
                transe.append(0) 
                tim += 1 
                retour -= 1 
            if tim < 12: 
                transe.append(1) 
    for trace in transe:  # Cumul Transposition 
        tom += 1 
        if trace == 1: 
            vrai += tom 
        else: 
            faux += tom 
    print('transe', b_, transe, 'V/F', vrai, faux) 
 
# Formes numérales des gammes 
gammes = [[1, 1, 0, 1, 1, 1, 0], [0, 2, 0, 1, 1, 1, 0], [2, 0, 0, 1, 1, 1, 0], 
          [4, 0, 0, 0, 0, 1, 0], [1, 0, 1, 1, 1, 1, 0], [0, 1, 1, 1, 1, 1, 0], 
          [1, 0, 3, 0, 0, 1, 0], [1, 2, 1, 0, 0, 1, 0], [2, 2, 0, 0, 0, 1, 0], 
          [0, 0, 1, 2, 1, 1, 0], [1, 3, 0, 0, 0, 1, 0], [0, 0, 2, 1, 1, 1, 0], 
          [1, 2, 2, 0, 0, 0, 0], [0, 0, 4, 0, 0, 1, 0], [1, 4, 0, 0, 0, 0, 0], 
          [1, 0, 0, 2, 1, 1, 0], [0, 1, 0, 2, 1, 1, 0], [1, 1, 3, 0, 0, 0, 0], 
          [0, 0, 0, 3, 1, 1, 0], [1, 1, 0, 0, 2, 1, 0], [0, 2, 0, 0, 2, 1, 0], 
          [0, 2, 0, 2, 0, 1, 0], [2, 0, 0, 0, 2, 1, 0], [1, 0, 1, 0, 2, 1, 0], 
          [1, 0, 1, 2, 0, 1, 0], [1, 1, 1, 2, 0, 0, 0], [2, 0, 0, 3, 0, 0, 0], 
          [0, 0, 2, 0, 2, 1, 0], [1, 2, 0, 2, 0, 0, 0], [1, 0, 0, 3, 0, 1, 0], 
          [1, 0, 0, 1, 2, 1, 0], [1, 1, 0, 3, 0, 0, 0], [1, 1, 2, 1, 0, 0, 0], 
          [0, 1, 0, 0, 3, 1, 0], [0, 0, 1, 0, 3, 1, 0], [0, 0, 0, 1, 3, 1, 0], 
          [0, 0, 0, 2, 2, 1, 0], [1, 0, 0, 0, 3, 1, 0], [0, 0, 2, 2, 0, 1, 0], 
          [0, 0, 0, 0, 4, 1, 0], [0, 0, 2, 3, 0, 0, 0], [1, 0, 0, 4, 0, 0, 0], 
          [0, 0, 0, 5, 0, 0, 0], [1, 1, 0, 1, 0, 2, 0], [1, 1, 0, 1, 2, 0, 0], 
          [0, 2, 0, 1, 0, 2, 0], [0, 2, 0, 1, 2, 0, 0], [2, 0, 0, 1, 0, 2, 0], 
          [2, 0, 0, 1, 2, 0, 0], [1, 0, 1, 1, 0, 2, 0], [1, 0, 1, 1, 2, 0, 0], 
          [1, 1, 0, 0, 1, 2, 0], [1, 1, 0, 0, 3, 0, 0], [1, 1, 0, 2, 1, 0, 0], 
          [1, 1, 2, 0, 1, 0, 0], [0, 2, 0, 0, 0, 3, 0], [1, 0, 0, 2, 2, 0, 0], 
          [1, 0, 0, 1, 0, 3, 0], [1, 3, 0, 0, 1, 0, 0], [1, 0, 0, 0, 1, 3, 0], 
          [0, 0, 0, 3, 0, 2, 0], [0, 0, 2, 1, 2, 0, 0], [1, 0, 0, 0, 0, 4, 0], 
          [0, 0, 0, 3, 2, 0, 0], [1, 1, 0, 0, 0, 3, 0], [3, 0, 0, 0, 0, 2, 0]] 
# Forme orales des gammes 
"""Moins(-), plus(+), par(x), rond(°), puis(^), dim(*)""" 
diaton = ['0', '-2', '+2', '^2', '-3', '-23', '-34x', '+34', '+23x', '-34', 'x3', 
          '°3', '+34x', '°34x', '^3', '-4', '-24', '^4', '°4', '-5', '-25', '-25+', 
          '+25-', '-35', '-35+', '+45x', '+25x', '°35-', '+35x', '-45+', '-45', 
          'x5', 'x45+', '-25°', '-35°', '-45°', '°45-', '°5', '°35+', '*5', '°35x', 
          '-45x', '°45x', '-6', '+6', '-26', '-26+', '+26-', '+26', '-36', '-36+', 
          '-56', '-56+', '+56', 'x46+', '-26°', '-46+', '-46°', 'x36+', '-56°', 
          '°46-', '°36+', '*6', '°46+', '°6', 'x26-'] 
# Tonalités à altération induite & Couple à signe unique... 
"""'-23'|Le signe s'applique à '2' et '3', d'ou '-2'&'-3'""" 
simple = ['-23', '+34', '-34', '-24', '-25', '-35', '-45', 
          '-26', '-36', '-56', '+56'] 
# L'altéractivité du double signe intégré ou hors série... 
""" Signe intégré induction '+34x' ou étendu '^2'""" 
# Les altérations utilisées 
signes = ['+', 'x', '^', '-', '°', '*'] 
# Composition tonale 
"""Domaine d'investigation & Opérateur variable""" 
tonale = ['1 4°', '* ^', '6° 6°']  # 1 = Tonalité nulle 
partie = [] 
for ton in tonale: 
    longer = len(ton) 
    double = [] 
    if ' ' not in ton: 
        gobeur = [ton]  # Format Liste Stand 
        partie.append(gobeur) 
    else: 
        """Détection vide""" 
        i = vide = 0 
        while 1: 
            if ton[i] == ' ': 
                vide = i 
                # Compter les vides ? 
            if i == longer - 1: 
                break 
            i += 1 
        double.append(ton[:vide]) 
        double.append(ton[vide+1:]) 
        print('double', double) 
    partie.append(double) 
    # break 
print() 
print('tonale', tonale) 
print('Partie', partie) 
for p in partie: 
    if len(p) != 1:  # Liste Format Dual 
        print('Pp2', p) 
        x = 0 
        for dia in diaton: 
            if p[0] in dia: 
                fiches(x, dia) 
            if p[1] in dia: 
                fiches(x, dia) 
            x += 1 
    else: 
        print('Pp1', p) 
        x = 0 
        for dia in diaton:  # Liste Format Simple 
            if str(p[0]) in dia: 
                fiches(x, dia) 
            x += 1
Avatar de
https://www.developpez.com
Le 11/11/2018 à 8:00
Bonjour
La leçon au sujet de l'octave numérique s'accompagne d'un tutoriel codé Python.

Un tableau d'accompagnement, réunissant la suite régulière des octaves parmi les nombres, a été préalablement produit élémentairement. Soit que les opérations réalisées pour parvenir à ce résultat, sont des plus sommaires (papier et crayon).

L'objectif est de calculer avec d'autres termes le même sujet, et en démontrant la véracité produite:
  1. Choix total
  2. Par fixation: Du point initial fixe, et du premier intervalle mesuré
  3. Par définition: Définition de l'engrenage diatonique


Code : Sélectionner tout 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#!/usr/bin/env python3.7
# -*- coding: utf-8 -*-
# Leçon musique: Octave numérique
# Pour une série régulière
octaves = [45, 129, 213, 297, 381, 465, 549, 633, 717,
           801, 885, 969, 1053, 1137, 1221, 1305, 1389,
           1473, 1557, 1641, 1725, 1809, 1893, 1977, 2061]
opus = [45, 129]
interval = []
# On peut choisir
"""Que demander ?
    0: Tout voir
    1: Par fixation
    2: Par définition"""
choix = 1
if choix in (0, 1):
    # Opus élément fixe
    # Diva fraction opus
    # Intervalle mémoire
    for o in range(len(opus)):
        diva = opus[o] / opus[0]
        interval.append(diva)
    # Différence intervalle opus
    dif_a = interval[1] - interval[0]
    # Intervalle fixe
    t = opus[0]
    for o in range(len(octaves)):
        print('octaves', octaves[o], ' |o| ', t)
        t = opus[0] * (interval[1] + (dif_a * o))
        # t = round(t)
if choix in (0, 2):
    value = 12  # Composants d'octave
    parts = 7   # Unité forte
    issue = 45  # Poids fort
    grade = 0   # Niveau d'octave
    for o in range(len(octaves)):
        vrai = issue + ((value * parts) * grade)
        print('octaves', octaves[o], ' |v| ', vrai)
        grade += 1
print('interval =', interval)


 Poster un commentaire
Developpez.com décline toute responsabilité quant à l'utilisation des différents éléments téléchargés.