IV. Fonction▲
On sait maintenant écrire des programmes Python avancés, mais ils vont vite devenir longs en nombre de lignes de code. De plus, on risque très vite de se retrouver avec des répétitions de codes similaires. Ce chapitre décrit le concept de fonction grâce auquel on va pouvoir écrire du code plus compact, lisible et réutilisable. On a déjà pu en utiliser dans les chapitres précédents, et on va ici voir comment en définir.
IV-A. Définition et appel de fonction▲
Une fonction se définit avec le mot réservé def, suivi de son nom, d'une liste de paramètres (qui peut être vide), du caractère deux-points (:) et enfin d'un bloc de code représentant son corps. Une fois définie, elle peut être utilisée autant de fois qu'on le souhaite, en l'appelant.
On peut classifier les fonctions selon deux critères. Une fonction peut renvoyer une valeur ou non, au terme de son exécution, et une fonction peut admettre ou non des paramètres. On va maintenant voir comment définir et utiliser ces différents types de fonctions.
IV-A-1. Liste de paramètres▲
Commençons avec un exemple d'une fonction qui ne renvoie pas de valeur, et n'admet aucun paramètre. Écrivons, par exemple, une fonction qui affiche la table de multiplication de kitxmlcodeinlinelatexdvp7finkitxmlcodeinlinelatexdvp. Pour cela, on va évidemment utiliser une boucle while qui va parcourir les entiers de kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp à kitxmlcodeinlinelatexdvp10finkitxmlcodeinlinelatexdvp. La fonction se définit comme suit :
2.
3.
4.
5.
def table7():
n = 1
while n <= 10:
print(n, "x 7 =", n * 7)
n += 1
Ces lignes de code définissent donc une fonction dont le nom est table7. La fonction initialise une variable n à kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp, puis une boucle se répète tant que la condition n <= 10 est vraie. Le corps de la boucle affiche une ligne de la table de multiplication, puis incrémente la valeur de n d'une unité. Pour exécuter cette fonction, il suffit simplement d'utiliser son nom, suivi d'une parenthèse ouvrante et d'une fermante. L'instruction d'appel de fonction table7() produit donc le résultat suivant :
1 x 7 = 7
2 x 7 = 14
3 x 7 = 21
4 x 7 = 28
5 x 7 = 35
6 x 7 = 42
7 x 7 = 49
8 x 7 = 56
9 x 7 = 63
10 x 7 = 70Un fichier Python est analysé par l'interpréteur ligne par ligne. Dès lors, un appel de fonction ne peut pas se faire avant que celle-ci n'ait été définie, sans quoi l'interpréteur génèrera une erreur vous signalant qu'il ne parvient pas à trouver la fonction demandée :
Traceback (most recent call last):
File "program.py", line 1, in <module>
table7()
NameError: name 'table7' is not definedImaginons maintenant que l'on souhaite aussi afficher la table de multiplication de kitxmlcodeinlinelatexdvp3finkitxmlcodeinlinelatexdvp, mais aussi celle de kitxmlcodeinlinelatexdvp8finkitxmlcodeinlinelatexdvp et pourquoi pas celle de kitxmlcodeinlinelatexdvp42finkitxmlcodeinlinelatexdvp. La manière la plus directe consiste à définir des fonctions table3, table8 et table42, mais ce n'est pas forcément la plus propre, car on va écrire plusieurs fois un code très similaire.
IV-A-1-a. Fonction à un paramètre▲
Bien évidemment, cela n'est absolument pas pratique de devoir ainsi recopier du code sur lequel on ne fait finalement que de petits changements. Il y a essentiellement deux endroits où on doit effectuer un changement, à savoir dans l'instruction print(n, "x 7 =", n * 7) où il faut remplacer les deux 7.
La solution qu'on va suivre consiste à faire en sorte que la fonction admette un paramètre, qui indique le nombre dont on veut la table de multiplication. Un paramètre est identifié par un nom, que l'on place entre les parenthèses de la définition de fonction. Voici une fonction table qui admet un paramètre base et qui affiche sa table de multiplication :
2.
3.
4.
5.
def table(base):
n = 1
while n <= 10:
print(n, "x", base, "=", n * base)
n += 1
Le corps de cette fonction est très similaire à celui de la fonction table7, les occurrences de 7 ayant été remplacées par base. Le grand avantage de cette fonction est qu'elle est beaucoup plus générique, c'est-à-dire qu'elle pourra fonctionner dans beaucoup plus de cas. Pour l'appeler, on utilise de nouveau son nom, sans oublier de fournir une valeur à son paramètre, entre parenthèses. Voici comment afficher successivement les tables de multiplication de kitxmlcodeinlinelatexdvp3finkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvp8finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp42finkitxmlcodeinlinelatexdvp :
2.
3.
table(3)
table(8)
table(42)
Lors de l'appel table(3), la fonction table est donc appelée et son paramètre base va se voir affecter la valeur spécifiée lors de l'appel, c'est-à-dire l'entier kitxmlcodeinlinelatexdvp3finkitxmlcodeinlinelatexdvp. C'est ce qu'on appelle le passage de paramètres qui a lieu lors d'un appel de fonction. C'est comme si on avait l'instruction base = 3 au début du corps de la fonction table. On peut d'ailleurs rendre cela plus explicite en écrivant l'appel ainsi :
table(base=3)
On reviendra plus loin dans ce chapitre sur cette notation particulière, qu'on a d'ailleurs déjà rencontrée lors d'appels de la méthode print, avec les paramètres nommés sep et end.
IV-A-1-a-i. Fonction à plusieurs paramètres▲
Une fonction peut évidemment admettre plus d'un paramètre. Il suffit simplement de les séparer par des virgules, autant dans la définition de la fonction que lors de son appel. Modifions, par exemple, la fonction table afin de pouvoir choisir la première ligne à afficher, et le nombre de lignes que l'on veut en tout :
2.
3.
4.
5.
def table(base, start, length):
n = start
while n < start + length:
print(n, "x", base, "=", n * base)
n += 1
La fonction admet trois paramètres, et il faut en spécifier trois lors de son appel. Voici le résultat de l'appel table(8, 5, 2), où on voit que la première ligne commence bien à kitxmlcodeinlinelatexdvp5finkitxmlcodeinlinelatexdvp et qu'il y en a bien deux affichées :
5 x 8 = 40
6 x 8 = 48De nouveau, on peut rendre explicite le passage des paramètres lors de l'appel de la fonction :
table(base=8, start=5, length=2)
De manière générale, cette notation est à éviter, car elle alourdit inutilement le code. Néanmoins, on verra, à la section suivante, qu'elle est nécessaire dans un cas particulier.
IV-A-1-a-ii. Valeur par défaut des paramètres▲
Dès lors qu'une fonction admet plusieurs paramètres, on doit également en fournir autant qu'il faut lors de son appel. Par exemple, on doit fournir trois paramètres lorsqu'on appelle notre dernière version de la fonction table. Si on tente de l'appeler comme on faisait au début, à savoir avec table(8), par exemple, on aura une erreur :
2.
3.
4.
Traceback (most recent call last):
File "program.py", line 7, in <module>
table(8)
TypeError: table() missing 2 required positional arguments: 'start' and 'length'
Pour autoriser un tel appel, il faut que les paramètres start et length possèdent une valeur par défaut, c'est-à-dire celle qu'ils auront lors de l'appel si on n'en spécifie pas une autre. En Python, c'est simple, il suffit de déclarer ces valeurs par défaut lors de la définition de la fonction :
2.
3.
4.
5.
def table(base, start=1, length=10):
n = start
while n < start + length:
print(n, "x", base, "=", n * base)
n += 1
Le paramètre start a donc kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp comme valeur par défaut et le paramètre length a kitxmlcodeinlinelatexdvp10finkitxmlcodeinlinelatexdvp comme valeur par défaut. On peut appeler cette fonction de plusieurs manières différentes :
table(8, 5, 2)
- On peut ne fournir une valeur que pour le premier paramètre, les deux autres recevant leur valeur par défaut :
table(8)
- On peut ne modifier que la valeur par défaut du paramètre start ou length, mais dans le deuxième cas, on doit nommer le paramètre qu'on veut modifier, car on ne suit pas l'ordre de la définition de la fonction :
2.
table(8, 5)
table(8, length=2)
Notez que les paramètres pour lesquels on prévoit une valeur par défaut doivent impérativement se trouver après les paramètres sans valeur par défaut, sans quoi l'interpréteur génèrera une erreur.
IV-A-1-b. Valeur de retour▲
Pour le moment, les fonctions qu'on est capable d'écrire admettent éventuellement des paramètres et permettent d'exécuter plusieurs instructions. Une fois la fonction exécutée, le programme continue son exécution en poursuivant juste après l'instruction d'appel de la fonction.
Une fonction peut également renvoyer une valeur qu'il est possible de récupérer lorsqu'on l'appelle. Commençons par voir un exemple d'une fonction qui calcule le produit de deux nombres. Contrairement aux fonctions précédemment vues, cette fonction va effectuer le calcul, mais n'affichera pas le résultat :
2.
def multiply(a, b):
return a * b
La fonction multiply admet donc deux paramètres a et b. Elle calcule ensuite leur produit qui est le résultat que doit produire la fonction. Pour signaler cela, on utilise le mot réservé return qui permet de définir la valeur de retour d'une fonction.
On peut appeler cette fonction comme on l'a fait jusqu'à présent, et donc écrire une instruction comme :
multiply(7, 9)
Cette instruction est valable et son exécution ne produira pas d'erreur. La fonction calcule le produit entre kitxmlcodeinlinelatexdvp7finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp9finkitxmlcodeinlinelatexdvp puis renvoie le résultat de ce calcul. Mais on ne récupère pas cette valeur renvoyée lors de l'appel, et dès lors ce dernier est complètement inutile. Le résultat calculé par la fonction est tout simplement perdu à jamais.
Pour avoir accès à la valeur de retour, il faut la stocker dans une variable lors de l'appel, en écrivant par exemple :
2.
res = multiply(7, 9)
print(res)
L'exécution de ces deux instructions affiche 63. La première instruction appelle la fonction multiply et stocke la valeur renvoyée par cet appel dans la variable res, c'est-à-dire la valeur de l'expression qui suit l'instruction return à la fin du corps de la fonction (return a * b). Cette valeur est ensuite affichée par la fonction print.
IV-A-1-b-i. Appel de fonction comme expression▲
L'appel d'une fonction qui renvoie une valeur est une expression, et on peut dès lors l'utiliser partout là où une expression est acceptée. Par exemple, on aurait pu écrire l'exemple précédent comme suit :
print(multiply(7, 9))
On pourrait aussi, par exemple, réécrire la fonction table en utilisant la fonction multiply pour calculer les différents produits :
2.
3.
4.
5.
def table(base, start=1, length=10):
n = start
while n < start + length:
print(n, "x", base, "=", multiply(n, base))
n += 1
On reviendra plus loin dans ce cours sur cette façon de programmer, à savoir en exploitant au maximum les fonctions.
IV-A-1-c. Le type function▲
Enfin, un dernier point intéressant à savoir est qu'une fonction est une valeur, en ce sens qu'il existe un type de donnée fonction. On peut s'en rendre compte en faisant appel à la fonction type.
Par exemple, si on exécute l'instruction suivante : print(type(multiply)), on obtient le résultat qui suit :
<class 'function'>Cette particularité est très puissante comme en témoigne l'exemple présenté au listing de la figure 1, qui permet d'afficher des tables de calcul (d'addition ou de multiplication). Le fichier functions.py contient avant tout les définitions des deux fonctions add et multiply.
Ensuite, on retrouve la définition de la fonction table, quelque peu modifiée par rapport à la précédente version. Celle-ci admet deux nouveaux paramètres qui sont un symbole (un caractère) et une opération à appliquer (une fonction). Par défaut, le symbole est un astérisque (*) et l'opération à appliquer est la fonction multiply.
Viennent enfin deux exemples d'appels à cette nouvelle version de la fonction table :
- le premier appel affiche la table de multiplication de kitxmlcodeinlinelatexdvp4finkitxmlcodeinlinelatexdvp, en commençant avec kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp (la valeur par défaut) et en affichant kitxmlcodeinlinelatexdvp2finkitxmlcodeinlinelatexdvp lignes ;
- le second appel affiche la « table d'addition » de kitxmlcodeinlinelatexdvp4finkitxmlcodeinlinelatexdvp en commençant également avec kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp (la valeur par défaut), affiche kitxmlcodeinlinelatexdvp5finkitxmlcodeinlinelatexdvp lignes, et utilise le symbole + et la fonction add pour l'opération à appliquer.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
def add(a, b):
return a + b
def multiply(a, b):
return a * b
def table(base, start=1, length=10, symbol="*", op=multiply):
n = start
while n < start + length:
print(n, symbol, base, "=", op(n, base))
n += 1
table(4, length=2)
table(4, length=5, symbol="+", op=add)
L'exécution du programme du listing précédent affiche ce qui suit à l'écran. On y voit clairement les deux lignes de la table de multiplication et les cinq lignes de la « table d'addition » :
1 * 4 = 4
2 * 4 = 8
1 + 4 = 5
2 + 4 = 6
3 + 4 = 7
4 + 4 = 8
5 + 4 = 9IV-A-1-d. Variable locale et globale▲
Lorsqu'on travaille avec des fonctions, il faut distinguer deux sortes de variables : les locales et les globales. Une variable globale est définie pour tout le programme ; elle est initialisée en dehors de toute fonction. Une variable locale est définie uniquement dans le corps d'une fonction, celle où elle a été initialisée. Pour comprendre ce qu'implique l'existence de ces deux sortes de variables, analysons le programme suivant :
2.
3.
4.
5.
6.
7.
def tvac(amount):
n = 1 + taxrate / 100
return amount * n
taxrate = 21
n = 25
print(tvac(n))
Les trois premières lignes définissent une fonction tvac qui transforme un prix hors taxe en un prix toutes taxes incluses. Le seul paramètre qu'elle admet est le montant hors taxe à transformer. Les trois dernières lignes calculent ce que donnent kitxmlcodeinlinelatexdvp25finkitxmlcodeinlinelatexdvp€ avec un taux de taxation de kitxmlcodeinlinelatexdvp21finkitxmlcodeinlinelatexdvp%. Le résultat de l'exécution est tout simplement :
30.25Lors de l'exécution de ce programme, il y a en fait deux variables n qui vont exister en même temps :
- Celle initialisée à la deuxième ligne est une variable locale à la fonction tvac. Elle n'existe que dans le corps de la fonction, durant le temps où elle est exécutée et disparait ensuite de la mémoire.
- Celle initialisée à l'avant-dernière instruction est une variable globale. Elle existe dans tout le programme, depuis son initialisation jusque la fin de l'exécution du programme.
Le concept de variable locale permet d'utiliser plusieurs variables différentes avec le même nom, pour autant qu'elles soient dans des fonctions différentes. Dans notre exemple, on a ainsi pu utiliser le nom n dans la fonction tvac, même si une variable globale de même nom existait déjà. Une conséquence immédiate est que la variable globale n n'est plus accessible dans la fonction tvac, au profit de la variable locale portant le même nom. Par contre, comme vous pouvez le voir sur l'exemple, la fonction tvac peut tout à fait accéder à la variable globale taxrate.
IV-A-1-d-i. Portée de variable▲
La portée d'une variable représente les endroits du code où on peut l'utiliser, c'est-à-dire où elle existe. Pour bien comprendre la différence entre les deux sortes de variables, et cette notion de portée de variable, voyons quelques exemples additionnels.
Tentons d'abord d'accéder à une variable locale en dehors de la fonction qui l'a initialisée :
2.
3.
4.
5.
def fun():
a = 12
fun()
print(a)
L'exécution de ce code provoquera une erreur, car la variable a dont on veut imprimer la valeur n'existe tout simplement pas à cet endroit dans le code. La portée de la variable est limitée au corps de la fonction où elle est initialisée, la variable disparait de la mémoire une fois que l'appel de la fonction est terminé :
Traceback (most recent call last):
File "program.py", line 5, in <module>
print(a)
NameError: name 'a' is not definedVoyons maintenant un deuxième exemple où on accède à une variable globale depuis une fonction :
2.
3.
4.
5.
def fun():
print(a)
a = 12
fun()
La variable globale a est initialisée à la valeur kitxmlcodeinlinelatexdvp12finkitxmlcodeinlinelatexdvp. Ensuite, la fonction fun est appelée, et affiche la valeur de cette variable, également disponible à cet endroit du code puisque c'est une variable globale.
Voyons maintenant un exemple où une fonction initialise une variable locale portant le même nom qu'une variable globale :
2.
3.
4.
5.
6.
7.
def fun():
a = 42
print("dans fun :", a)
a = 12
fun()
print("en dehors de fun :", a)
Il y a donc deux variables avec le nom a : une globale initialisée à kitxmlcodeinlinelatexdvp12finkitxmlcodeinlinelatexdvp et une locale à la fonction fun initialisée à kitxmlcodeinlinelatexdvp42finkitxmlcodeinlinelatexdvp. En fonction de où on se situe dans le code, on accèdera donc à l'une ou l'autre, en se rappelant que la variable locale masque la variable globale. L'exécution du programme affiche donc :
dans fun : 42
en dehors de fun : 12Voyons enfin un dernier exemple qui ne se comporte pas forcément comme on pourrait le croire de prime abord. Dans une fonction, on va commencer par tenter un accès à la variable globale a, pour ensuite initialiser une variable locale de même nom et y accéder :
2.
3.
4.
5.
6.
7.
def fun():
print("globale :", a)
a = 42
print("locale :", a)
a = 12
fun()
L'exécution de ce code produit l'erreur suivante :
Traceback (most recent call last):
File "program.py", line 7, in <module>
fun()
File "program.py", line 2, in fun
print("globale :", a)
UnboundLocalError: local variable 'a' referenced before assignmentL'interpréteur Python signale que la variable locale a est utilisée avant d'avoir été initialisée. Elle existe donc, mais ne possède pas de valeur. Lorsqu'une fonction contient des variables locales, elles masquent les variables globales de même nom dans tout le corps de la fonction.
IV-A-1-d-ii. Modifier une variable globale▲
Comment modifier la valeur d'une variable globale depuis une fonction ? Si on utilise une instruction d'affectation, cela va créer une nouvelle variable locale de même nom. Pour signaler qu'un nom réfère à une variable globale, il suffit d'utiliser le mot réservé global :
2.
3.
4.
5.
6.
7.
def fun():
global a
a = 42
a = 12
fun()
print(a)
Comme on verra plus loin, retenez néanmoins que ce n'est pas une bonne pratique d'utiliser des variables globales et qu'il faut limiter au maximum leur utilisation ainsi que celle du mot réservé global.
IV-A-1-e. Instruction return▲
Revenons un moment sur l'instruction return qui permet donc de définir la valeur de retour d'une fonction. En plus de cet effet, elle permet également d'arrêter l'exécution de la fonction et de poursuivre l'exécution du programme après son appel. Tout code se trouvant après un return ne sera donc pas exécuté. Par exemple, la seconde instruction de la fonction suivante ne sera jamais exécutée :
2.
3.
def fun():
return 42
print('This will not be printed')
Le fait que return arrête l'exécution de la fonction peut parfois être utilisé pour simplifier son code. Écrivons par exemple une fonction abs qui calcule la valeur absolue d'un nombre qu'on lui passe en paramètre. Voici une première version de cette fonction :
2.
3.
4.
5.
def abs(x):
if x < 0:
return -x
else:
return x
Lorsque la valeur de x est négative, la condition du if est satisfaite, et la première instruction return est exécutée. Ensuite, le corps de la fonction est quitté, les instructions se trouvant après le return n'étant pas exécutées. On peut dès lors simplifier le code de la fonction, en éliminant l'instruction else, inutile :
2.
3.
4.
def abs(x):
if x < 0:
return -x
return x
Cela permet de diminuer le niveau d'indentation d'une partie du code et de le raccourcir d'une ligne, ce qui le rend plus lisible. Une autre pratique que l'on retrouve parfois consiste à diminuer le nombre total de return dans une fonction. Cela permet notamment une analyse plus aisée, puisqu'on diminue ainsi le nombre de points de sortie :
2.
3.
4.
def abs(x):
if x < 0:
x = -x
return x
IV-B. Découpe en sous-problèmes▲
À quoi servent les fonctions en pratique ? Comme on a pu le constater, elles permettent de réutiliser du code et évitent ainsi de la duplication, tout en rendant le programme plus lisible. Les fonctions permettent également de structurer un programme, fournissant ainsi une documentation implicite de ce dernier.
Lorsque vous devez écrire du code très similaire à du code déjà écrit, on pourrait sans doute croire que la meilleure solution consiste à copier-coller un bout de code, puis de l'adapter. Il s'agit pourtant d'une très mauvaise pratique, pour deux raisons principales :
- les chances de se tromper à un moment lors des copier-coller ou des adaptations de ces derniers sont grandes ;
- si une erreur est détectée dans le code qui a été copié-collé, il va falloir la corriger partout là où ce code a été copié-collé.
IV-B-1. Décomposition▲
Le second intérêt des fonctions est de structurer un programme. Grâce à ces dernières, on va pouvoir découper un gros programme en petits blocs, chacun plus simple à comprendre. Voyons cela avec l'exemple suivant qui permet d'afficher les kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp premiers nombres premiers (pour rappel, un nombre naturel kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp est premier s'il admet exactement deux diviseurs distincts (qui seront dès lors kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp)) :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
n = 1
nb = 10
while nb > 0:
divisors = 0
d = 1
while d <= n:
if n % d == 0:
divisors += 1
d += 1
if divisors == 2:
print(n)
nb -= 1
n += 1
Comprendre ce programme sans être celui qui l'a écrit n'est pas du tout facile. Tout d'abord, il n'y a aucun commentaire permettant d'aider le lecteur et le nom de toutes les variables n'est pas forcément explicite. Ensuite, ce code contient deux boucles imbriquées, ce qui rend sa compréhension moins aisée, de prime abord.
Afin de rendre le programme plus clair, il faut définir et utiliser des fonctions. Pour cela, on va décomposer le problème qu'on nous demande de résoudre en sous-problèmes. On peut en identifier trois :
- tester si un nombre est un diviseur d'un autre ;
- tester si un nombre est premier ;
- afficher les kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp premiers nombres premiers.
Une fois ces sous-problèmes résolus, on pourra les combiner pour résoudre le problème principal. Commençons par définir une fonction isDivisor permettant de tester si un nombre est un diviseur d'un autre :
2.
def isDivisor(d, n):
return n % d == 0
Pour tester si le nombre d est un diviseur de n, il suffit de vérifier si le reste de la division entière de n par d est nul ou non. Le corps de la fonction est simplement composé d'une instruction qui renvoie un booléen (True si d est un diviseur de n et False sinon).
Il nous faut ensuite une fonction isPrime qui permet de tester si un nombre n est un nombre premier ou non :
2.
3.
4.
5.
6.
7.
8.
def isPrime(n):
d = 1
nbDivisors = 0
while d <= n:
if isDivisor(d, n):
nbDivisors += 1
d += 1
return nbDivisors == 2
La fonction compte le nombre de diviseurs que possède le nombre n. Pour cela, elle parcourt tous les nombres compris entre kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp, et teste, grâce à la fonction isDivisor précédemment définie, s'ils divisent ou non n. On termine en vérifiant que le nombre de diviseurs distincts doit être de deux, en renvoyant donc un booléen (True si n est un nombre premier et False sinon).
Enfin, il nous reste maintenant à définir une fonction printPrimes qui permet d'afficher des nombres premiers. Pour cela, on va parcourir tous les nombres naturels l'un après l'autre, et afficher les nombres premiers, jusqu'à en avoir affiché suffisamment. Le listing suivant montre le programme final, où l'on peut voir la fonction printPrimes qui utilise la fonction isPrime précédemment définie.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
# Programme d'affichage d'une séquence de nombres premiers
# Auteur : Sébastien Combéfis
# Version : 24 aout 2015
def isDivisor(d, n):
return n % d == 0
def isPrime(n):
d = 1
nbDivisors = 0
while d <= n:
if isDivisor(d, n):
nbDivisors += 1
d += 1
return nbDivisors == 2
def printPrimes(nb):
n = 1
while nb > 0:
if isPrime(n):
print(n)
nb -= 1
n += 1
printPrimes(7)
L'exécution du programme présenté au listing précédent affiche donc la séquence des sept premiers nombres premiers :
2
3
5
7
11
13
17Découper un problème en sous-problèmes, et par conséquent définir plusieurs fonctions de plus petites tailles, permet de rendre un programme plus lisible. Il s'agit de manière générale d'un bon réflexe à suivre. Il ne faut pas avoir peur de définir plusieurs petites fonctions, même si leur corps ne fait qu'une instruction.
De plus, les différentes fonctions définies pourraient être réutilisées dans d'autres programmes ultérieurs. En procédant de la sorte, on se constitue un stock de fonctions à utiliser pour en définir de nouvelles.
IV-B-1-a. Spécification▲
Lorsqu'on définit des fonctions, c'est évidemment dans le but de les utiliser. Il est donc très important de les documenter, c'est-à-dire d'ajouter des commentaires expliquant ce qu'elles font, et comment les utiliser. On pourrait par exemple écrire :
2.
3.
4.
# Fonction permettant de tester si le nombre entier d
# est un diviseur du nombre entier n
def isDivisor(d, n):
return n % d == 0
Ce commentaire qu'on a ajouté décrit ce que fait la fonction, ainsi que les paramètres qu'il faut lui fournir. Il est donc complet et permet d'utiliser la fonction comme il faut.
On peut décrire une fonction de manière plus systématique en fournissant sa spécification. Pour cela, on doit décrire deux choses :
- les préconditions d'une fonction sont toutes les conditions qui doivent être satisfaites avant de pouvoir appeler la fonction, que ce soit sur des variables globales ou sur ses paramètres ;
- les postconditions d'une fonction sont toutes les conditions qui seront satisfaites après appel de la fonction, si les préconditions étaient satisfaites, que ce soit sur des variables globales ou sur l'éventuelle valeur renvoyée.
Voyons tout de suite comment spécifier la fonction isDivisor en définissant ses préconditions et postconditions :
2.
3.
4.
5.
6.
7.
# Test de la divisibilité d'un nombre par un autre
# Pre : d et n sont deux entiers positifs
# d != 0
# Post : la valeur renvoyée vaut True si d divise n,
# et False sinon
def isDivisor(d, n):
return n % d == 0
Pour appeler la fonction, il faut donc lui fournir deux nombres entiers positifs en paramètres, et s'assurer que d soit différent de zéro. Dans ce cas, après avoir appelé la fonction, la valeur qu'elle aura renvoyée contiendra True si d est un diviseur de n et False sinon.
La spécification d'une fonction contient donc toute la documentation nécessaire pour l'utiliser correctement. S'il ne faut pas devoir lire le corps de la fonction pour comprendre ce qu'elle fait et comment l'utiliser, c'est que la spécification est bien écrite.
IV-C. Récursion▲
Dans tous les exemples qu'on a vu pour le moment, on a défini des fonctions, puis on les a appelées, que ce soit depuis une autre fonction ou en dehors de toute fonction. On peut également appeler une fonction depuis son propre corps. Une telle fonction, qui s'appelle elle-même, est appelée fonction récursive.
Commençons par voir un exemple pratique où une telle fonction peut s'avérer utile. Supposons que l'on veuille écrire une fonction permettant de calculer la somme kitxmlcodeinlinelatexdvp1 + 2 + ... + nfinkitxmlcodeinlinelatexdvp pour un entier positif n donné. On pourrait utiliser une boucle while pour ce faire et écrire :
2.
3.
4.
5.
6.
def sum(n):
result = 0
while n > 0:
result += n
n -= 1
return result
Cette fonction est tout à fait correcte et calcule la valeur qu'il faut. On peut également l'écrire différemment, à l'aide d'une fonction récursive, en se rendant compte de la propriété suivante :
kitxmlcodelatexdvp\sum_{i = 1}^n i = \left( \sum_{i = 1}^{n - 1} i \right) + n,finkitxmlcodelatexdvpqui indique donc que la somme des kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp premiers entiers positifs correspond à la somme des kitxmlcodeinlinelatexdvpn - 1finkitxmlcodeinlinelatexdvp premiers entiers positifs à qui on ajoute kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp. De plus, lorsque kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp vaut 1, on obtient directement la valeur de la somme qui est kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp. Étant donné ces deux observations, on peut réécrire la fonction sum comme suit :
Une fonction récursive agit donc comme une boucle, puisqu'elle se rappelle elle-même un certain nombre de fois. Pour éviter une boucle infinie, il faut que dans un cas, appelé cas de base, la fonction ne se rappelle pas. Dans notre exemple, le cas de base se produit lorsque kitxmlcodeinlinelatexdvpn = 1finkitxmlcodeinlinelatexdvp, et le cas récursif pour kitxmlcodeinlinelatexdvpn > 1finkitxmlcodeinlinelatexdvp. La figure 3 montre l'enchainement des appels récursifs qui se produisent lorsqu'on exécute sum(3).
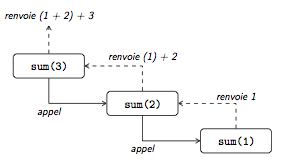
Les fonctions récursives peuvent parfois grandement améliorer la lisibilité du code, et sont parfois plus facile à concevoir lorsque le problème à résoudre s'y prête bien. Dès lors que la résolution d'un problème peut être faite en résolvant une version simplifiée du problème initial, il y a lieu de penser à la récursion.
Dans notre cas, la somme des kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvp premiers entiers positifs peut être connue en utilisant le résultat de la somme des kitxmlcodeinlinelatexdvpn - 1finkitxmlcodeinlinelatexdvp premiers nombres entiers, problème plus simple à résoudre.
Prenons un autre exemple, à savoir une fonction qui calcule rapidement la valeur de kitxmlcodeinlinelatexdvpa^nfinkitxmlcodeinlinelatexdvp. Pour cela, on va se baser sur les propriétés mathématiques suivantes :
kitxmlcodelatexdvpa^n = \left\{ \begin{array}{ll} a & \textrm{si $n$ = 1} \\ (a^2)^{n/2} & \textrm{si $n$ est pair} \\ a \cdot (a^2)^{(n - 1) / 2} & \textrm{si $n > 2$ et $n$ est impair} \end{array} \right.finkitxmlcodelatexdvpCette méthode de calcul est appelée exponentiation rapide. Le premier cas correspond au cas de base, et les deux cas suivants sont des cas récursifs. Voici la fonction récursive pow qui traduit directement en code ces trois propriétés :
IV-D. Module▲
Terminons ce chapitre en voyant comment définir ses propres modules. On a déjà vu comment importer un module et en utiliser les fonctions dans les chapitres précédents, en particulier à la section 3.4, où on a découvert le module turtle.
L'intérêt d'un module est de pouvoir y définir des fonctions que l'on va facilement pouvoir réutiliser dans d'autres programmes, ou dans d'autres modules. L'un des buts d'une fonction étant d'être réutilisée, il est dès lors important d'avoir une structure telle que le module dans un langage de programmation.
IV-D-1. Utilisation d'un module▲
Revoyons rapidement comment utiliser un module. La première chose à faire consiste à importer le module grâce au mot réservé import. On peut importer un module complètement ou uniquement en importer certaines fonctions. Dans le premier cas, il faudra préfixer chaque appel de fonction par le nom du module duquel elle provient. On peut par exemple écrire le programme suivant :
2.
3.
4.
import turtle
turtle.forward(90)
turtle.done()
L'autre solution importe directement des fonctions depuis des modules et on peut ainsi les appeler directement, juste avec leur nom. Le programme précédent peut se réécrire comme suit :
2.
3.
4.
from turtle import forward, done
forward(90)
done()
Comme on l'a déjà vu, on peut ne pas lister explicitement toutes les fonctions à importer et simplement écrire from turtle import *. Si on fait cela, il faudra faire attention aux conflits de noms, c'est-à-dire si plusieurs modules importés contiennent des fonctions portant le même nom. De manière générale, on essaie dès lors d'éviter d'importer *, sauf lorsqu'on est certain qu'aucun conflit de noms peut se produire. Si vous n'importez, par exemple, qu'un seul module, cela ne pose aucun souci.
IV-D-1-a. Définition d'un module▲
La définition d'un module est très facile en Python, il suffit essentiellement de créer un fichier .py contenant des définitions de fonctions. Un module peut évidemment lui-même importer d'autres modules.
Créons par exemple un module shapes contenant des fonctions pour dessiner des formes à l'aide d'une tortue. Le listing suivant montre le code de ce module. On peut y voir une fonction polygon qui permet de dessiner des polygones réguliers et une fonction square pour dessiner des carrés. Dans les deux cas, on peut spécifier la longueur des côtés et la couleur du trait (noir par défaut). Pour les polygones, on doit en plus préciser le nombre de côtés voulu.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
# Module shapes de dessin de formes avancées
# à l'aide d'une tortue
# Auteur : Sébastien Combéfis
# Version : 25 aout 2015
from turtle import *
def polygon(nbsides, side, col='black'):
color(col)
angle = 360 / nbsides
i = 0
while i < nbsides:
forward(side)
left(angle)
i += 1
def square(side, col='black'):
polygon(4, side, col)
Ce fichier, étant enregistré sous le nom shapes.py, définit un module shapes dont on peut importer les fonctions. Par exemple, pour dessiner trois polygones de couleurs différentes en utilisant ce module, il suffit d'écrire le programme suivant :
2.
3.
4.
5.
6.
7.
from shape import *
square(90)
polygon(6, 90, 'red')
polygon(10, 90, 'blue')
done()
Afin que Python puisse retrouver les différents modules existants, on ne peut pas les placer n'importe où sur sa machine. On ne va pas ici rentrer dans les détails techniques de où l'interpréteur Python cherche les modules, le plus facile étant de placer le fichier du module dans le même dossier que le fichier de votre script.
IV-D-1-b. Documentation▲
Comme on a pu le voir précédemment, il est important d'ajouter un commentaire explicatif pour chaque fonction, afin de savoir ce qu'elle fait et comment l'utiliser. C'est évidemment encore plus important dans le cadre d'un module puisque le but est qu'il soit réutilisé par vous-même ou par d'autres programmeurs.
Pour cela, on va utiliser une forme spéciale de commentaires qui permettra d'automatiquement générer la documentation d'un module Python, appelée Docstring (PEP 0257). Le principe consiste à déclarer un littéral de type chaine de caractères comme première instruction du corps de la fonction documentée. Par convention, on délimite les littéraux avec des triples guillemets doubles, qui permettent d'écrire la chaine de caractères sur plusieurs lignes.
Voici deux exemples, dont un avec une documentation sur une seule ligne et l'autre avec une documentation sur plusieurs lignes :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
def sum(n):
"""Renvoie la somme des entiers de 1 à n (compris)."""
if n == 1:
return 1
return sum(n - 1) + n
def isDivisor(d, n):
"""Teste la divisibilité d'un nombre par un autre.
Pre : d et n sont deux entiers positifs
d != 0
Post : la valeur renvoyée vaut True si d divise n,
et False sinon
"""
return n % d == 0


