III. Instruction de contrôle▲
Dans tout programme, à un moment donné, il faut rompre l'exécution séquentielle des instructions, comme on a pu le voir dans les exemples intuitifs du premier chapitre. Ce chapitre présente deux types d'instruction permettant de briser cette exécution linéaire. Les instructions conditionnelles permettent de n'exécuter une partie du programme que si une condition donnée est satisfaite. Les instructions répétitives permettent de répéter un certain nombre de fois une portion de code.
III-A. Type booléen▲
On connait déjà deux types de données : les nombres (entiers, flottants et complexes) et les chaines de caractères. Voyons maintenant le type booléen dont les données ne peuvent prendre que deux valeurs différentes : vrai et faux. Un intérêt de ce type de donnée est de pouvoir prendre des décisions dans un programme en définissant des conditions qui seront satisfaites ou non.
En Python, on peut utiliser les mots réservés True et False qui représentent les deux valeurs booléennes possibles. Ces deux valeurs sont du type bool comme on peut le vérifier avec la fonction type.
On peut, par exemple, écrire :
2.
3.
4.
v = True
print(v)
print(type(v))
L'exécution de ce programme affiche :
True
<class 'bool'>III-A-1. Opérateur de comparaison▲
On ne va évidemment pas se contenter des littéraux True et False, mais on va vouloir construire des expressions booléennes. Pour cela, une première façon de faire consiste à utiliser un opérateur de comparaison. Il en existe au total six en Python, repris à la figure 1.
|
Description |
Notation |
|---|---|
|
Égal |
|
|
Différent |
|
|
Strictement plus petit |
|
|
Plus petit ou égal |
|
|
Strictement plus grand |
|
|
Plus grand ou égal |
|
Ces opérateurs permettent de comparer deux valeurs et de tester si elles sont égales ou différentes, ou de savoir si l'une est (strictement) plus petite ou plus grande que l'autre. L'exemple suivant illustre l'utilisation de quelques-uns de ces opérateurs :
2.
3.
a = 12 == 3 * 4 # a vaut True
b = "Eat" > "Drink" # b vaut True
c = a != b # c vaut False
La première expression compare deux nombres entiers. La valeur de 12 étant égale à la valeur de l'expression 3 * 4, la variable a reçoit la valeur True. La deuxième expression compare deux chaines de caractères. Comme Eat est strictement plus grand que Drink (il se trouve après dans l'ordre alphabétique), la variable b reçoit la valeur True. Enfin, la troisième expression compare deux booléens. La valeur de la variable a n'étant pas différente de la valeur de la variable b, la variable c reçoit la valeur False.
De manière générale, on ne peut comparer que des valeurs qui sont du même type. Pour comparer deux valeurs de types différents, il faut avant tout effectuer des conversions explicites. Dans l'exemple suivant, qui compare un nombre entier et une chaine de caractères, la première instruction produit une erreur tandis que la seconde, où une conversion explicite en chaine de caractères a eu lieu, est valide :
>>> 19 > 'Hello'
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unorderable types: int() > str()
>>> str(19) > 'Hello'
FalseIII-A-1-a. Opérateur logique▲
Une seconde façon de construire des expressions booléennes consiste à en combiner plusieurs pour en construire une nouvelle, en utilisant des opérateurs logiques. Python propose trois opérateurs logiques repris à la figure 2.
|
Description |
Notation |
|---|---|
|
« non » logique |
|
|
« et » logique |
|
|
« ou » logique |
|
Le premier opérateur logique permet d'inverser la valeur d'une expression booléenne. Appliquée à une expression booléenne qui vaut True, elle produit donc comme valeur False, et inversement :
a = not 8 > 2 # a vaut False
La valeur de l'expression 8 > 2 valant True, puisque kitxmlcodeinlinelatexdvp8finkitxmlcodeinlinelatexdvp est strictement plus grand que kitxmlcodeinlinelatexdvp2finkitxmlcodeinlinelatexdvp, la valeur de l'expression not 8 > 2 vaut donc False.
Les deux autres opérateurs logiques combinent deux expressions booléennes. Le résultat du « et » logique ne vaut True que si les deux expressions combinées valent True, et il vaut False sinon. Le résultat du « ou » logique vaut True si au moins une des deux expressions combinées vaut True, et il vaut False sinon.
La figure 3 résume les résultats de ces deux opérateurs, sous la forme d'un tableau appelé table de vérité. Une telle table fournit la valeur d'expressions booléennes composées pour toutes les combinaisons possibles des expressions booléennes sur base desquelles elles sont construites.
|
a |
b |
a |
a |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Voici deux exemples d'expressions booléennes complexes construites avec des opérateurs logiques :
2.
a = 8 > 2 and 12 <= 4 # a vaut False
b = 5 != 5 or 'PY' == 'P' + 'Y' # b vaut True
Dans la première expression, la valeur de l'expression à gauche de l'opérateur and est True puisque kitxmlcodeinlinelatexdvp8finkitxmlcodeinlinelatexdvp est strictement plus grand que kitxmlcodeinlinelatexdvp2finkitxmlcodeinlinelatexdvp, mais celle de l'expression à droite vaut False puisque kitxmlcodeinlinelatexdvp12finkitxmlcodeinlinelatexdvp n'est pas plus petit ou égal à kitxmlcodeinlinelatexdvp4finkitxmlcodeinlinelatexdvp. Dès lors, la variable a reçoit la valeur False puisque les deux expressions combinées par l'opérateur logique and ne valent pas toutes les deux True.
Pour la seconde expression, l'expression à gauche de l'opérateur or vaut False puisque kitxmlcodeinlinelatexdvp5finkitxmlcodeinlinelatexdvp n'est pas différent de kitxmlcodeinlinelatexdvp5finkitxmlcodeinlinelatexdvp, et celle de l'expression à droite vaut True puisque la chaine de caractères PY est bien égale à la concaténation des chaines P et Y. Puisqu'au moins une des deux expressions combinées par le or vaut True, la variable b vaut True.
III-A-1-a-i. Propriété de court-circuit▲
Lorsque l'interpréteur Python évalue une expression booléenne contenant des opérateurs and et or, il le fait de manière fainéante, en court-circuitant parfois l'expression à droite de l'opérateur logique. Ce qui se passe, c'est que parfois, en connaissant la valeur de l'expression à gauche de l'opérateur, peu importe celle de l'expression de droite, le résultat final peut déjà être connu.
Si on regarde attentivement les tables de vérité, on se rend compte que si la valeur de a est False, alors a and b vaut False peu importe la valeur de b. De même, si la valeur de a est True, alors a or b vaut True peu importe la valeur de b. Voici deux exemples illustrant cette propriété de court-circuit :
2.
a = False and c # a vaut False, peu importe la valeur de c
b = True or c # b vaut True, peu importe la valeur de c
III-A-1-b. Priorité▲
Tout comme les opérateurs arithmétiques vus précédemment, les opérateurs de comparaison et les opérateurs logiques possèdent un certain niveau de priorité. Ces opérateurs sont effectués après tout ceux qu'on a déjà rencontrés, dans l'ordre suivant :
- les quatre comparaisons : <, <=, > et >= ;
- les égalités : == et != ;
- le « non » logique :
not; - le « et » logique : and ;
- le « ou » logique :
or.
De nouveau, on peut utiliser les parenthèses pour rendre explicite l'ordre dans lequel vous souhaitez qu'une expression soit évaluée. La figure 4 montre quelques exemples d'expressions ainsi que l'expression complètement parenthésée équivalente.
|
Expression |
Complètement parenthésée |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III-A-1-c. Enchainement de comparaisons▲
Enfin, on peut enchainer les opérateurs de comparaison pour effectuer deux opérations de comparaison qui ont en commun une valeur. Prenons, par exemple, une variable x dont on voudrait savoir si sa valeur est comprise entre kitxmlcodeinlinelatexdvp0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp20finkitxmlcodeinlinelatexdvp. Pour cela, on peut écrire :
check = 0 <= x <= 20
Ce que l'interpréteur va faire, c'est effectuer les comparaisons une à une, les combinant avec un « et » logique. L'instruction ci-dessus équivaut donc à l'expression suivante :
check = 0 <= x and x <= 20
Ce type d'enchainement d'opérateurs de comparaison peut se faire avec n'importe quel opérateur. On peut par exemple écrire l'expression suivante :
2 == x < 4
III-B. Instruction conditionnelle▲
Maintenant que l'on maitrise les expressions booléennes, on va pouvoir les utiliser pour n'exécuter une partie de programme que si une certaine condition est satisfaite grâce aux instructions conditionnelles.
III-B-1. Instruction if▲
Commençons avec un exemple qui teste la valeur d'une variable x et affiche une phrase seulement si cette valeur est négative :
2.
3.
4.
x = -5
if x <= 0:
print("x est négatif !")
print("Sa valeur absolue vaut ", -x)
L'exécution de ce programme produit la sortie suivante :
x est négatif !
Sa valeur absolue vaut 5L'instruction if se compose du mot réservé if suivi d'une condition, puis du caractère deux-points (:) et enfin d'une séquence d'instructions à exécuter si la valeur de la condition est vraie. Comme vous l'avez remarqué, pour distinguer les instructions à exécuter si la condition est satisfaite, elles sont indentées, c'est-à-dire précédées de plusieurs espaces. La figure 5 montre l'organigramme correspondant à ce programme.
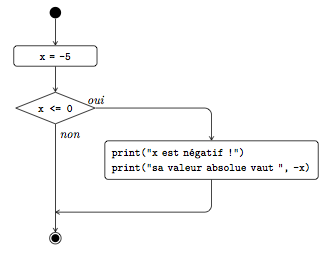
Toutes les instructions à exécuter si la condition est satisfaite forment un ensemble appelé bloc de code. Elles doivent toutes être indentées de la même manière, par exemple avec une tabulation horizontale ou avec deux espaces, sans quoi une erreur se produira. Si l'on se réfère au guide de style de Guido van Rossum, il faut utiliser quatre espaces par niveau d'indentation.
La condition d'une instruction if est généralement une expression booléenne. Si la valeur de l'expression est True, la condition est satisfaite et le bloc de code du if est exécuté, sinon il est ignoré. Dans tous les cas, le programme continue ensuite son exécution après l'instruction if.
III-B-1-a. Exécution alternative▲
En plus d'un bloc de code qui n'est exécuté que si une condition est satisfaite, on peut également définir un second bloc qui ne sera exécuté que dans le cas contraire, c'est-à-dire si la condition n'est pas satisfaite. Une telle exécution alternative se déclare avec le mot réservé else.
Voici un exemple de programme qui utilise une instruction if-else :
2.
3.
4.
5.
grade = 9.5
if grade >= 10:
print("vous avez réussi")
else:
print("vous avez raté")
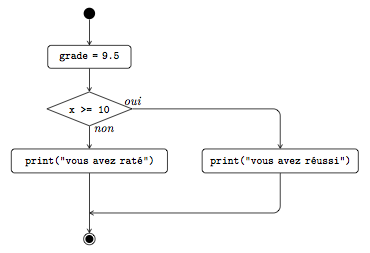
Le bloc if sera donc exécuté si la condition placée après le mot réservé if est satisfaite, et sinon, c'est le bloc else qui sera exécuté. Ensuite, le programme continue son exécution après l'instruction if-else. La figure 6 montre l'organigramme correspondant à ce programme.
III-B-1-b. Imbrication d'instructions▲
Avec ce qu'on vient de voir, on peut donc définir une ou deux branches d'exécution différentes, en fonction de la valeur d'une condition. Comment pourrait-on faire si on désire plus de deux branches ?
Supposons que l'on souhaite écrire un programme qui contrôle la température de l'huile d'un moteur d'une voiture. Tant que celle-ci est sous les kitxmlcodeinlinelatexdvp100^\circfinkitxmlcodeinlinelatexdvpC, tout est normal, si elle est entre kitxmlcodeinlinelatexdvp100^\circfinkitxmlcodeinlinelatexdvpC et kitxmlcodeinlinelatexdvp130^\circfinkitxmlcodeinlinelatexdvpC, il faut émettre un avertissement et enfin si elle dépasse les kitxmlcodeinlinelatexdvp130^\circfinkitxmlcodeinlinelatexdvpC, il faut faire retentir une alarme de danger.
Pour cela, on va utiliser deux instructions if-else que l'on va imbriquer l'une dans l'autre. Ce qu'on va faire, c'est qu'on va utiliser comme contenu du bloc else de la première instruction if-else, une seconde instruction if-else :
2.
3.
4.
5.
6.
7.
8.
temp = 126
if temp < 100:
print("tout va bien")
else:
if 100 <= temp <= 130:
print("attention")
else:
print("danger")
La figure 7 montre l'organigramme de ce programme. Les deux instructions if-else y sont encadrées, ce qui fait bien ressortir qu'elles sont imbriquées l'une dans l'autre. La seconde a été imbriquée dans le bloc else, mais on aurait très bien pu la placer dans le bloc if si on voulait. La raison pour laquelle on ne l'a pas fait est que Python propose une écriture simplifiée lorsque l'imbrication se fait dans le bloc else.
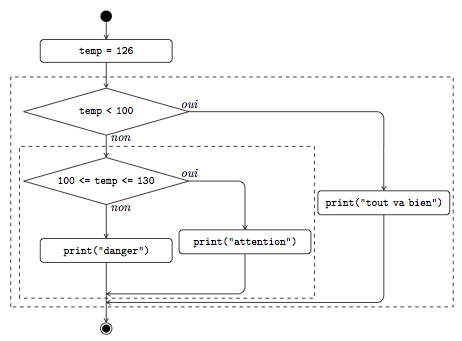
Vous aurez remarqué que comme le contenu du bloc else est une instruction if-else, cette dernière doit être indentée. Par conséquent, les instructions des blocs if et else de cette dernière ont un niveau d'indentation double. Si on continue à ajouter d'autres branches, on va se retrouver avec des niveaux d'indentation trop grands. Pour éviter cela, Python propose l'instruction elif (contraction de else if) permettant une écriture simplifiée des instructions conditionnelles à plus de deux branches. L'exemple précédent se réécrit comme suit :
2.
3.
4.
5.
6.
7.
temp = 126
if temp < 100:
print("tout va bien")
elif 100 <= temp <= 130:
print("attention")
else:
print("danger")
On est maintenant capable d'écrire un programme complet pour chercher les racines d'un trinôme du second degré, dont le code se trouve au listing suivant. Faites attention aux commentaires qui ont été utilisés, ainsi qu'à la mise en page globale du code.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
# Programme de recherche des racines d'un trinôme
# du second degré de la forme ax^2 + bx + c
# Auteur : Sébastien Combéfis
# Version : 7 aout 2015
from math import sqrt
print("Recherche des racines de ax^2 + bx + c")
a = int(input("Coefficient a : "))
b = int(input("Coefficient b : "))
c = int(input("Coefficient c : "))
# Calcul du discriminant
delta = b**2 - 4 * a * c
print("Discriminant :", delta)
# Test des trois cas possibles et affichage des racines du trinôme
if delta < 0:
print("Pas de racine réelle")
elif delta == 0:
x = -b / (2 * a)
print("Une racine réelle double :", x)
else:
x1 = (-b - sqrt(delta)) / (2 * a)
x2 = (-b + sqrt(delta)) / (2 * a)
print("Deux racines réelles distinctes:", x1, "et", x2)
III-C. Instruction répétitive▲
Une grande force de la programmation, et l'une des raisons pour lesquelles elle a été inventée, c'est de pouvoir répéter plusieurs fois la même tâche. Voyons maintenant comment exécuter plusieurs fois une même portion de code à l'aide d'instructions répétitives.
III-C-1. Instruction while▲
Commençons avec un exemple qui affiche les cinq premiers nombres naturels, en commençant avec kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp :
2.
3.
4.
n = 1
while n <= 5:
print(n)
n += 1
L'exécution de ce programme produit la sortie suivante :
1
2
3
4
5L'instruction while se compose du mot réservé while suivi d'une condition, puis du caractère deux-points (:) et enfin d'un bloc de code appelé corps de la boucle. Celui-ci est exécuté intégralement de manière répétée, tant que la condition du while est vraie. La figure 9 montre l'organigramme de ce programme, où la boucle ainsi créée apparait.
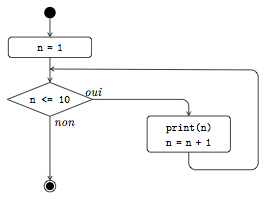
Tout comme pour l'instruction if, la condition d'une instruction while est généralement une expression booléenne. Le corps de la boucle est donc répété tant que la condition est satisfaite. Il est dès lors important que les variables qui apparaissent dans la condition voient leur valeur changer dans le corps de la boucle, sans quoi la condition ne changera jamais de valeur. Si celle-ci était vraie au départ, elle le restera donc toujours et on aura une boucle infinie. Voici un simple programme qui vous dira perpétuellement bonjour :
2.
while True:
print("Hello")
La première fois que la condition d'une boucle while est testée se fait avant même d'avoir exécuté une seule fois son corps. Il se peut donc qu'il ne soit jamais exécuté si la condition est fausse dès le départ.
Parfois, on souhaite néanmoins toujours exécuter un bloc de code, et on peut pour cela attacher un bloc else à l'instruction while. Le code contenu dans ce bloc else est exécuté une fois lorsque la condition du while devient fausse, avant que l'exécution ne continue après l'instruction while. L'exemple suivant illustre cela :
2.
3.
4.
5.
6.
n = 10
while n <= 5:
print(n)
n += 1
else:
print("La boucle est terminée")
L'exécution de ce programme produit la sortie suivante :
La boucle est terminéeDans ce cas-ci, la condition de la boucle est initialement fausse puisque kitxmlcodeinlinelatexdvp10finkitxmlcodeinlinelatexdvp n'est pas plus petit ou égal à kitxmlcodeinlinelatexdvp5finkitxmlcodeinlinelatexdvp. Le corps de la boucle ne va donc pas s'exécuter. Par contre, comme il y a un bloc else attaché à l'instruction while, il va être exécuté une fois. Comme ici la condition est initialement fausse, seul le contenu du bloc else sera donc exécuté, avant que l'exécution ne continue après l'instruction while.
III-C-1-a. Interruption de boucle▲
Une boucle se termine de manière naturelle lorsque sa condition devient fausse. Parfois, on peut vouloir la quitter prématurément, lorsqu'une autre condition est satisfaite. Python propose pour cela l'instruction break qui quitte directement une boucle, sans exécuter l'éventuel bloc else attaché à l'instruction while.
L'exemple suivant recherche le plus petit naturel non nul divisible par kitxmlcodeinlinelatexdvp38finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp46finkitxmlcodeinlinelatexdvp. Pour cela, on utilise une boucle qui parcoure toutes les valeurs entre kitxmlcodeinlinelatexdvp1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp1000000finkitxmlcodeinlinelatexdvp et, pour chacune d'elles, teste avec une instruction if si elle divise kitxmlcodeinlinelatexdvp38finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp46finkitxmlcodeinlinelatexdvp grâce à l'opérateur modulo (le reste de la division est nul si c'est un diviseur). Dans ce cas, on a trouvé la valeur que l'on cherche et on peut arrêter la boucle, grâce à l'instruction break :
2.
3.
4.
5.
6.
n = 1
while n <= 1000000:
if n % 38 == 0 and n % 46 == 0:
break
n += 1
print(n, "est le plus petit nombre divisible par 38 et 46")
La figure 10 montre l'organigramme de ce programme, où vous pouvez clairement voir les deux chemins d'exécution possibles quittant la boucle. On voit également très bien que l'instruction break« casse » la boucle.
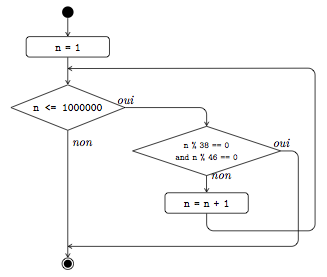
De manière générale, on peut se passer de l'instruction break en adaptant la condition de la boucle while. Au plus vous aurez de chemins d'exécution possibles, au plus votre code deviendra complexe à comprendre. Prenons, par exemple, la situation où votre boucle ne se termine pas quand elle le devrait. Afin de trouver le bug, il vous faudra examiner tous les chemins de sortie possibles, et il vaut donc mieux minimiser leur nombre. L'exemple précédent peut, par exemple, se réécrire comme suit, en intégrant la condition du if dans celle du while :
2.
3.
4.
n = 1
while n <= 1000000 and not (n % 38 == 0 and n % 46 == 0):
n += 1
print(n, "est le plus petit nombre divisible par 38 et 46")
Néanmoins, vous constaterez qu'on perd en lisibilité, la condition du while devenant complexe. Si l'on s'en réfère aux conventions, un code pythonique doit être concis et clair. Dans ce cas, la version du code avec l'instruction break est préférable.
Pour être complet, il faut également mentionner l'instruction continue. Celle-ci va faire en sorte d'interrompre l'exécution du corps de la boucle, et directement retourner à l'évaluation de la condition du while. Elle permet en quelque sorte de « passer un tour » de boucle. De nouveau, il est possible de s'en passer en modifiant le corps de la boucle. L'exemple suivant affiche tous les nombres pairs plus petits que kitxmlcodeinlinelatexdvp100finkitxmlcodeinlinelatexdvp :
2.
3.
4.
5.
6.
n = 0
while n <= 100:
n += 1
if n % 2 != 0:
continue
print(n)
La première instruction augmente la valeur de la variable n. Ensuite, si celle-ci est impaire (le reste de la division par deux n'est pas nul), on arrête d'exécuter le corps de la boucle et on passe directement au tour suivant. Sinon, on affiche la valeur de n.
III-D. Dessin avec turtle▲
Pour terminer ce chapitre, découvrons le module turtle qui permet d'effectuer simplement des dessins constitués de lignes. Ce module permet de réaliser des dessins en faisant se déplacer une tortue dans le plan, qui dessine le chemin qu'elle a parcouru. Voyons d'abord un programme qui utilise ce module avant d'en détailler le contenu :
2.
3.
4.
5.
6.
7.
8.
from turtle import *
i = 0
while i < 5:
forward(50)
left(72)
i += 1
done()
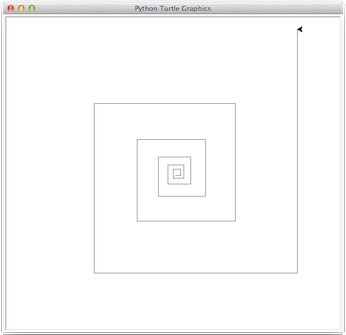
Ce programme comporte une boucle while qui s'exécute cinq fois. À chaque boucle, la tortue avance de kitxmlcodeinlinelatexdvp50finkitxmlcodeinlinelatexdvp unités (forward), puis tourne sur place de kitxmlcodeinlinelatexdvp72finkitxmlcodeinlinelatexdvp degrés (left), dans le sens antihorloger. La figure 11 montre le résultat de l'exécution du programme, sachant que la tortue se trouve initialement au milieu de la fenêtre, orientée vers la droite.
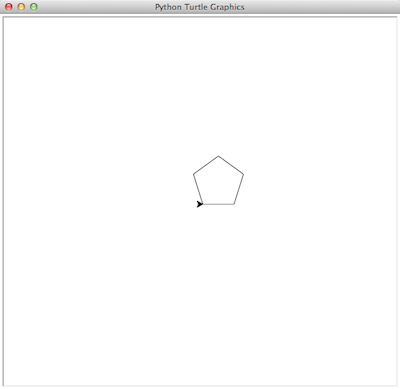
Une fois le module importé avec from turtle import *, on peut utiliser toutes les fonctions définies dans ce module, dont les principales sont reprises à la figure 12. La fonction forward permet d'avancer d'un nombre d'unités qu'on lui précise tandis que la fonction left permet de tourner sur place d'un angle en degrés qu'on lui précise également. La fonction done, appelée à la fin du programme, permet de garder la fenêtre de dessin ouverte, malgré que la tortue ait fini ses déplacements.
|
Fonction |
Description |
|---|---|
|
|
Avancer de la distance spécifiée |
|
|
Reculer de la distance spécifiée |
|
|
Tourne sur place dans le sens antihorloger de l'angle spécifié |
|
|
Tourne sur place dans le sens horloger de l'angle spécifié |
|
|
Relever le crayon |
|
|
Baisser le crayon |
|
|
Changer la couleur du crayon ( |
|
|
Changer l'épaisseur du crayon par l'épaisseur spécifiée |
|
|
Aller, en ligne droite, au point de coordonnées kitxmlcodeinlinelatexdvp(x, y)finkitxmlcodeinlinelatexdvp |
|
|
Effacer tout |
|
|
Maintenir la fenêtre ouverte une fois le dessin terminé |
Il faut faire attention à la fonction goto(x, y) qui permet de déplacer la tortue vers le point de coordonnées kitxmlcodeinlinelatexdvp(x, y)finkitxmlcodeinlinelatexdvp. En effet, les axes ne sont pas comme vous en avez l'habitude en mathématiques : le coin supérieur gauche se trouve en kitxmlcodeinlinelatexdvp(0, 0)finkitxmlcodeinlinelatexdvp, et l'axe des kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp va vers la droite tandis que l'axe des kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp descend vers le bas.
On observe également la présence des fonctions up() et down() qui permettent de lever et baisser le crayon, ce qui permet de dessiner ou non lorsque la tortue se déplace. D'autres fonctions sont disponibles, comme celle pour dessiner des arcs de cercle, par exemple, mais nous n'allons pas les détailler ici.
Le listing suivant montre un autre exemple complet de programme qui utilise une tortue pour réaliser un dessin. Le résultat de l'exécution de ce programme est présenté à la figure 14. Expérimentez ce programme en changeant les valeurs des variables MAX et factor.