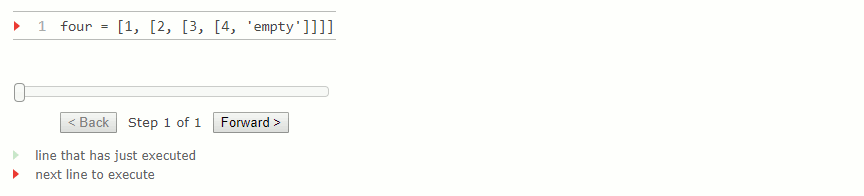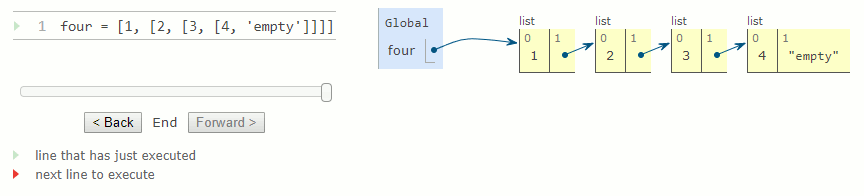Composition de programmes

Une valeur de type list est une séquence qui peut avoir une longueur arbitraire. Les listes ont un large ensemble de comportements intégrés, ainsi qu'une syntaxe spécifique pour exprimer ces comportements. Nous avons déjà vu la liste littérale, qui s'évalue à une instance de list, ainsi qu'une expression de sélection d'élément qui évalue une valeur dans la liste. La fonction intégrée len renvoie la longueur d'une séquence. Ci-dessous, digits est une liste comportant quatre éléments. L'élément à l'indice 3 est le second 8.

>>> digits = [1, 8, 2, 8]
>>> len(digits)
4
>>> digits[3]
8

De plus, les listes peuvent être additionnées et multipliées par des nombres entiers. Pour les séquences, l'addition et la multiplication n'additionnent ni ne multiplient les éléments, mais combinent et répliquent les séquences elles-mêmes. C'est-à-dire que la fonction add du module operator (et l'opérateur +) produit une liste qui est la concaténation des arguments ajoutés. La fonction mul du module operator (et l'opérateur *) peut prendre une liste et un entier k pour renvoyer la liste qui consiste en k répétitions de la liste d'origine.

>>> [2, 7] + digits * 2
[2, 7, 1, 8, 2, 8, 1, 8, 2, 8]

Une liste peut contenir toutes sortes de valeurs, y compris une autre liste. La sélection d'élément peut être appliquée à plusieurs reprises afin de sélectionner un élément profondément imbriqué dans une liste contenant des listes.

>>> pairs = [[10, 20], [30, 40]]
>>> pairs[1]
[30, 40]
>>> pairs[1][0]
30

Bien souvent, nous souhaitons itérer sur les éléments d'une séquence et effectuer un calcul pour chaque élément. Ce modèle est tellement courant que Python possède une instruction de contrôle supplémentaire pour traiter les données séquentielles : l'instruction for.

Considérons le problème de compter combien de fois une valeur apparaît dans une séquence. Nous pouvons implémenter une fonction pour calculer ce compte en utilisant une boucle while.

>>> def count(s, value):
        """Count the number of occurrences of value in sequence s."""
        total, index = 0, 0
        while index < len(s):
            if s[index] == value:
                total = total + 1
            index = index + 1
        return total

>>> count(digits, 8)
2

L'instruction Python for peut simplifier ce corps de fonction en itérant sur les valeurs des éléments directement sans utiliser de variable index.

>>> def count(s, value):
        """Count the number of occurrences of value in sequence s."""
        total = 0
        for elem in s:
            if elem == value:
                total = total + 1
        return total

>>> count(digits, 8)
2

L'instruction for comprend une seule clause de la forme :

for <name> in <expression>:
    <suite>

L'instruction for est exécutée par la procédure suivante :

1. Évaluez l'<expression> de l'en-tête, qui doit générer une valeur itérative.

2. Pour chaque élément dans cette valeur itérative, dans l'ordre :

   1. Liez <nom> à cette valeur dans la trame actuelle.
   2. Exécutez la <suite>.

Cette procédure d'exécution se réfère à des valeurs itérables. Les listes sont un type de séquence, et les séquences sont des valeurs itérables. Leurs éléments sont considérés dans leur ordre séquentiel. Python possède d'autres types itérables, mais nous nous concentrerons sur les séquences pour l'instant. La définition générale du terme « itérable » apparaît dans la section sur les itérateurs du chapitre 4.

Une conséquence importante de cette procédure d'évaluation est que <nom> sera lié au dernier élément de la séquence après l'exécution de l'instruction for. La boucle for introduit une autre manière de mettre à jour l'environnement par une instruction.

Dépaquetage de séquence. Un modèle commun dans les programmes est d'avoir une séquence d'éléments qui sont eux-mêmes des séquences, mais ont tous une longueur fixe. Une déclaration peut inclure plusieurs noms dans son en-tête pour « dépaqueter » chaque séquence d'éléments dans ses éléments respectifs. Par exemple, nous pouvons avoir une liste de listes à deux éléments :

>>> pairs = [[1, 2], [2, 2], [2, 3], [4, 4]]

et souhaiter trouver le nombre de ces paires qui ont le même premier et deuxième élément :

>>> same_count = 0

L'instruction for suivante liera chaque nom x et y aux premier et second éléments de chaque paire, respectivement :

>>> for x, y in pairs:
        if x == y:
            same_count = same_count + 1

>>> same_count
2

Ce modèle de liaison de noms multiples à plusieurs valeurs dans une séquence à longueur fixe est parfois appelé dépaquetage ou décompactage de séquence ; c'est le même modèle que l'on voit dans les instructions d'affectation qui lient plusieurs noms à plusieurs valeurs.

Intervalles. Un intervalle est un autre type de séquence intégrée dans Python, qui représente un intervalle d'entiers consécutifs. Ces plages de nombres sont créées avec le mot-clef range, qui prend deux arguments entiers : le premier nombre de la série et le nombre immédiatement au-dessus du dernier nombre dans la plage souhaitée.

>>> range(1, 10)  # Comprend 1, mais pas 10
range(1, 10)

L'appel du constructeur de liste sur un intervalle s'évalue à une liste ayant les mêmes éléments que l’intervalle, afin que les éléments puissent être facilement inspectés.

>>> list(range(5, 8))
[5, 6, 7]

Si un seul argument est donné, il est interprété comme le majorant de la dernière valeur pour une plage qui commence à 0.

>>> list(range(4))
[0, 1, 2, 3]

Les intervalles apparaissent souvent dans l'en-tête d'une boucle for pour spécifier le nombre de fois que la suite de la boucle doit être exécutée : une convention commune consiste à utiliser un caractère de soulignement unique pour le nom dans l'en-tête lorsque le nom n'est pas utilisé dans le corps de la boucle :

>>> for _ in range(3):
        print('Go Bears!')

Go Bears!
Go Bears!
Go Bears!

Ce caractère de soulignement est juste un nom de variable comme un autre dans l'environnement du point de vue de l'interpréteur, mais il a pour les programmeurs une signification conventionnelle qui indique que ce nom n'apparaîtra pas ailleurs dans la boucle.

Les séquences sont une forme si commune de données composées que des programmes entiers sont souvent organisés autour de cette abstraction unique. Il est possible d'assembler des composants modulaires qui prennent des séquences en entrée et produisent d'autres séquences en sortie pour effectuer le traitement des données. On peut souvent définir des composants complexes en enchaînant un pipeline d'opérations élémentaires de traitement de séquences.

Listes en compréhension. De nombreuses opérations de traitement de séquence peuvent être exprimées en évaluant une expression fixe pour chaque élément dans une séquence et en collectant les valeurs résultantes dans une séquence de résultats. Dans Python, une liste en compréhension est une expression qui effectue un tel calcul :

>>> odds = [1, 3, 5, 7, 9]
>>> [x+1 for x in odds]
[2, 4, 6, 8, 10]

Le mot-clé for utilisé ci-dessus ne fait pas partie d'une boucle for, mais fait partie d'une liste en compréhension, car il se trouve entre crochets. La sous-expression x+1 est évaluée avec x lié à chaque élément de la liste odds des chiffres impairs à tour de rôle, et les valeurs résultantes sont collectées dans une liste.

Une autre opération de traitement de séquence commune consiste à sélectionner un sous-ensemble de valeurs qui satisfont certaines conditions. Les listes en compréhension peuvent également exprimer ce modèle, par exemple en sélectionnant tous les éléments de la liste odds qui sont des diviseurs de 25 .

>>> [x for x in odds if 25 % x == 0]
[1, 5]

La forme générale d'une liste en compréhension est la suivante :

[<map expression> for <name> in <sequence expression> if <filter expression>]

Pour évaluer une liste en compréhension, Python évalue la <sequence expression>, qui doit renvoyer une valeur itérative. Ensuite, pour chaque élément de la séquence, la valeur de l'élément est liée à <name>, l'expression <filter expression> est évaluée, et si elle donne une valeur réelle, l'expression <map expression> est évaluée. Les valeurs produites par <map expression> sont collectées dans une liste.

Un troisième motif commun dans le traitement de séquences est d'agréger toutes les valeurs d'une séquence en une seule valeur. Les fonctions intégrées sum, min et max sont autant d'exemples de fonctions d'agrégation.

En combinant les possibilités d'évaluation d'une expression pour chaque élément d'une liste, de sélection d'un sous-ensemble d'éléments et d'agrégation d'éléments, nous pouvons résoudre de nombreux problèmes en utilisant une approche de traitement de séquence.

Un nombre parfait est un nombre entier positif égal à la somme de ses diviseurs. Les diviseurs de n sont des nombres entiers positifs inférieurs à n qui divisent n sans reste. La liste des diviseurs de n peut se construire à l'aide d'une liste en compréhension.

>>> def divisors(n):
        return [1] + [x for x in range(2, n) if n % x == 0]

>>> divisors(4)
[1, 2]
>>> divisors(12)
[1, 2, 3, 4, 6]

En utilisant divisors, nous pouvons calculer tous les nombres parfaits de 1 à 1000 avec une autre liste en compréhension. (À noter que 1 est généralement considéré comme un nombre parfait, mais il ne passe pas le test avec notre définition de divisors.)

>>> [n for n in range(1, 1000) if sum(divisors(n)) == n]
[6, 28, 496]

Nous pouvons réutiliser notre définition de divisors pour résoudre un autre problème : trouver le périmètre minimum d'un rectangle ayant des longueurs de côtés entières, étant donné sa superficie. La superficie d'un rectangle est le produit de sa hauteur par sa largeur. Par conséquent, étant donné la superficie et la hauteur, nous pouvons calculer la largeur. Nous pouvons affirmer que la largeur et la hauteur sont des diviseurs de la superficie pour que les longueurs des côtés soient des nombres entiers.

>>> def width(area, height):
        assert area % height == 0
        return area // height

Le périmètre d'un rectangle est la somme de la longueur de ses côtés :

>>> def perimeter(width, height):
        return 2 * width + 2 * height

La hauteur d'un rectangle ayant des longueurs de côté entières doit être un diviseur de sa superficie. Nous pouvons calculer le périmètre minimum en considérant toutes les hauteurs possibles :

>>> def minimum_perimeter(area):
        heights = divisors(area)
        perimeters = [perimeter(width(area, h), h) for h in heights]
        return min(perimeters)

>>> area = 80
>>> width(area, 5)
16
>>> perimeter(16, 5)
42
>>> perimeter(10, 8)
36
>>> minimum_perimeter(area)
36
>>> [minimum_perimeter(n) for n in range(1, 10)]
[4, 6, 8, 8, 12, 10, 16, 12, 12]

Fonctions d'ordre supérieur. Les motifs communs que nous avons observés dans le traitement des séquences peuvent s'exprimer à l'aide de fonctions d'ordre supérieur. D'abord, l'évaluation d'une expression pour chaque élément dans une séquence peut se faire en appliquant une fonction à chaque élément :

>>> def apply_to_all(map_fn, s):
        return [map_fn(x) for x in s]

Il est possible de filtrer les éléments d'une liste pour lesquels une expression est vraie en appliquant une fonction à chaque élément.

>>> def keep_if(filter_fn, s):
        return [x for x in s if filter_fn(x)]

Enfin, on peut réaliser de nombreuses formes d'agrégation en appliquant répétitivement une fonction de deux arguments à la valeur réduite jusqu'à présent (reduced) et chaque élément à tour de rôle.

>>> def reduce(reduce_fn, s, initial):
        reduced = initial
        for x in s:
            reduced = reduce_fn(reduced, x)
        return reduced

Par exemple, reduce peut être utilisé pour multiplier entre eux tous les éléments d'une séquence. En utilisant mul comme reduce_fn et 1 comme valeur initiale, reduce permet de calculer le produit d'une séquence de nombres.

>>> reduce(mul, [2, 4, 8], 1)
64

Nous pouvons également trouver des nombres parfaits en utilisant ces fonctions d'ordre supérieur.

>>> def divisors_of(n):
        divides_n = lambda x: n % x == 0
        return [1] + keep_if(divides_n, range(2, n))

>>> divisors_of(12)
[1, 2, 3, 4, 6]
>>> from operator import add
>>> def sum_of_divisors(n):
        return reduce(add, divisors_of(n), 0)

>>> def perfect(n):
        return sum_of_divisors(n) == n

>>> keep_if(perfect, range(1, 1000))
[1, 6, 28, 496]

Noms conventionnels. Pour les informaticiens, une fonction comme apply_to_all s'appelle souvent map et la fonction keep_if s'appelle souvent filter. En Python, les fonctions intégrées map et filter sont des généralisations de ces fonctions qui ne renvoient pas des listes. Ces fonctions sont décrites dans un chapitre ultérieur. Les définitions ci-dessus sont équivalentes à l'application du constructeur de liste au résultat des fonctions intégrées map et filter :

>>> apply_to_all = lambda map_fn, s: list(map(map_fn, s))
>>> keep_if = lambda filter_fn, s: list(filter(filter_fn, s))

La fonction reduce est définie dans le module functools de la bibliothèque standard Python. Dans cette version, l'argument initial est facultatif :

>>> from functools import reduce
>>> from operator import mul
>>> def product(s):
        return reduce(mul, s)

>>> product([1, 2, 3, 4, 5])
120

Il est plus fréquent en Python d'utiliser directement les listes en compréhension plutôt que des fonctions d'ordre supérieur, mais les deux approches du traitement de séquences sont largement utilisées.

Nous avons introduit deux types de données natives qui satisfont l'abstraction des séquences : les listes et les plages. Tous deux satisfont les conditions avec lesquelles nous avons commencé cette section : longueur et sélection des éléments. Python possède deux autres comportements de types de séquence qui étendent l'abstraction de séquence.

Appartenance. Il est possible de tester si une valeur appartient à une séquence. Python a deux opérateurs in et not in qui renvoient True ou False selon que l'élément apparaît dans une séquence.

>>> digits
[1, 8, 2, 8]
>>> 2 in digits
True
>>> 1828 not in digits
True

Tranche. Les séquences contiennent des séquences plus petites en elles. Une tranche (slice) d'une séquence est une suite quelconque de valeurs contiguës de la séquence d'origine, désignée par une paire d'entiers. Comme pour le constructeur range, le premier entier indique l'indice de départ de la tranche et le second désigne l'élément suivant le dernier élément de la tranche.

En Python, les tranches de séquences s'expriment de manière analogue à la sélection des éléments, en utilisant des crochets. Un caractère deux-points sépare les indices de départ et de fin. Toute limite qui est omise est supposée être une valeur extrême : 0 pour l'index de départ et la longueur de la séquence pour l'indice de fin.

>>> digits
[1, 8, 2, 8]
>>> digits[0:2]
[1, 8]
>>> digits[1:]
[8, 2, 8]

Il est également possible d'utiliser des tranches sur les branches d'un arbre. Par exemple, nous voudrions peut-être placer une restriction sur le nombre de branches d'un arbre. Un arbre binaire est (récursivement) soit une feuille, soit une séquence d'au plus deux arbres binaires. Il est assez fréquent de vouloir binariser un arbre, c'est-à-dire calculer un arbre binaire à partir d'un arbre de départ en regroupant des branches adjacentes.

>>> def right_binarize(tree):
        """Construct a right-branching binary tree."""
        if is_leaf(tree):
            return tree
        if len(tree) > 2:
            tree = [tree[0], tree[1:]]
        return [right_binarize(b) for b in tree]

>>> right_binarize([1, 2, 3, 4, 5, 6, 7])
[1, [2, [3, [4, [5, [6, 7]]]]]]

L'énumération de ces comportements supplémentaires de l'abstraction séquence Python nous donne l'occasion de réfléchir à ce qui constitue une abstraction de données utile en général. La richesse d'une abstraction (c'est-à-dire le nombre de comportements qu'elle supporte) a des conséquences. Pour les utilisateurs d'une abstraction, des comportements supplémentaires peuvent être utiles. D'un autre côté, satisfaire toutes les exigences d'une abstraction riche avec un nouveau type de données peut être difficile. Une autre conséquence négative des abstractions riches est qu'elles sont plus longues à apprendre pour les utilisateurs.

Les séquences sont une abstraction riche parce qu'elles sont si omniprésentes en informatique que l'apprentissage de certains comportements complexes est justifié. En général, la plupart des abstractions définies par l'utilisateur doivent être gardées aussi simples que possible.

Lectures complémentaires. La syntaxe d'utilisation des tranches admet une grande variété de cas particuliers, tels que les valeurs initiales négatives, les valeurs de fin et le pas des valeurs intermédiaires. On pourra trouver une description complète dans la documentation officielle de Python 3. Voir aussi le chapitre sur les listes du livre Apprendre à programmer avec Python 3 de Gérard Swinnen disponible sur ce site. Dans ce chapitre, nous utiliserons uniquement les fonctions de base décrites ci-dessus.

Les valeurs textuelles sont peut-être plus fondamentales encore en informatique que les nombres. À titre d'exemple, les programmes Python sont écrits et stockés sous forme de texte. Le type de données natif pour le texte en Python s'appelle chaîne de caractères (string), ou souvent simplement chaîne (quand le contexte est clair), et correspond au constructeur str.

Il y a beaucoup de choses à dire sur la façon dont les chaînes sont représentées, exprimées et manipulées dans Python. Les chaînes sont un autre exemple d'une abstraction riche exigeant de la part du programmeur un investissement substantiel pour les maîtriser. Cette section sert d'introduction condensée aux comportements essentiels des chaînes.

Les chaînes littérales peuvent exprimer un texte arbitraire, et sont placées entre des apostrophes (ou guillemets simples) ou entre guillemets (doubles).

>>> 'I am string!'
'I am string!'
>>> "I've got an apostrophe"
"I've got an apostrophe"
>>> '您好'
'您好'

Nous avons déjà vu des chaînes dans notre code, sous la forme de docstrings, dans les appels à la fonction print et en tant que messages d'erreur dans les instructions de type assert.

Les chaînes satisfont les deux conditions de base d'une séquence que nous avons introduites au début de cette section : elles ont une longueur et elles permettent la sélection d'éléments.

>>> city = 'Berkeley'
>>> len(city)
8
>>> city[3]
'k'

Les éléments d'une chaîne sont eux-mêmes des chaînes qui n'ont qu'un seul caractère. Un caractère est une seule lettre de l'alphabet, un signe de ponctuation ou autre symbole. Contrairement à beaucoup d'autres langages de programmation, Python n'a pas de type caractère distinct ; tout texte est une chaîne, et les chaînes qui représentent des caractères uniques ont une longueur de 1.

Comme les listes, les chaînes peuvent également être combinées par addition et multiplication.

>>> 'Berkeley' + ', CA'
'Berkeley, CA'
>>> 'Shabu ' * 2
'Shabu Shabu '

Appartenance. En Python, le comportement des chaînes diverge d'autres types de séquences. L'abstraction de chaîne n'est pas entièrement conforme à l'abstraction de séquence que nous avons décrite pour les listes et les intervalles. En particulier, l'opérateur d'appartenance s'applique aux chaînes, mais a un comportement totalement différent que lorsqu'il est appliqué à des séquences. Il reconnaît des sous-chaînes et non des éléments individuels.

>>> 'here' in "Where's Waldo?"
True

Chaînes littérales multilignes. Les chaînes ne se limitent pas forcément à une seule ligne. Des guillemets triples permettent de créer des chaînes littérales qui comportent plusieurs lignes. Nous avons déjà utilisé ces guillemets triples pour les docstrings.

>>> """The Zen of Python
claims, Readability counts.
Read more: import this."""
'The Zen of Python\nclaims, "Readability counts."\nRead more: import this.'

Dans le résultat affiché ci-dessus, le \n (« barre oblique inverse et lettre n ») est un élément unique qui représente une nouvelle ligne. Bien qu'il apparaisse comme deux caractères (barre oblique inverse et « n »), il est considéré comme un seul caractère dans la détermination de la longueur d'une chaîne et pour la sélection d'un élément.

Coercition de chaîne. Une chaîne peut être créée à partir d'un objet Python quelconque en appelant la fonction str avec un objet comme argument. Cette fonctionnalité des chaînes est utile pour la construction de chaînes descriptives à partir d'objets de différents types.

>>> str(2) + ' is an element of ' + str(digits)
'2 is an element of [1, 8, 2, 8]'

Lectures complémentaires. L'encodage de texte dans les ordinateurs est un sujet complexe. Dans ce chapitre, nous résumons la façon dont les chaînes sont représentées et omettons de nombreux détails. Toutefois, pour de nombreuses applications, les informations particulières sur la façon dont les chaînes sont encodées par les ordinateurs sont des connaissances essentielles. On pourra trouver une description complète dans la documentation officielle de Python 3. Voir aussi la section sur les chaînes de caractères du livre Apprendre à programmer avec Python 3 de Gérard Swinnen ou le chapitre sur les chaînes de caractères du livre Pensez en Python d'Allen B. Downey également disponible en français sur ce site.

Notre capacité à utiliser des listes comme éléments d'autres listes fournit un nouveau moyen de combinaison dans notre langage de programmation. Cette capacité s'appelle une propriété de fermeture d'un type de données. En général, une méthode pour combiner des valeurs de données a une propriété de fermeture si le résultat de la combinaison peut être combiné à son tour en utilisant la même méthode. La fermeture est la clé de la puissance expressive dans toutes les formes de combinaison, car elle nous permet de créer des structures hiérarchiques – des structures constituées de pièces, elles-mêmes composées de pièces, et ainsi de suite.

Nous pouvons visualiser les listes dans les diagrammes d'environnement à l'aide de la notation boîte-et-pointeur. Une liste est représentée sous la forme de boîtes adjacentes contenant les éléments de la liste. Les valeurs natives telles que les nombres, les chaînes, les valeurs booléennes et None apparaissent dans une boîte élémentaire. Les valeurs composites, telles que les valeurs de fonction et d'autres listes, sont indiquées par une flèche.

Jusqu'à présent, nous n'avons utilisé que des types natifs pour représenter des séquences. Cependant, nous pouvons également développer des représentations séquentielles qui ne sont pas intégrées dans Python. Une liste chaînée est une représentation commune d'une séquence construite à partir de paires imbriquées. Le diagramme d'environnement ci-dessous illustre la représentation sous la forme d'une liste chaînée d'une séquence de quatre éléments contenant les chiffres 1, 2, 3 et 4.

Une liste chaînée est une paire contenant le premier élément de la séquence (dans ce cas 1) et le reste de la séquence (dans ce cas une représentation de 2, 3, 4). Le deuxième élément est également une liste chaînée. Le reste de la liste la plus imbriquée contenant seulement 4 est 'empty', une valeur qui représente une liste chaînée vide.

Les listes chaînées ont une structure récursive : le reste d'une liste chaînée est une liste chaînée ou 'empty'. Nous pouvons définir une représentation abstraite des données pour valider, construire et sélectionner les composants des listes chaînées.

>>> empty = 'empty'
>>> def is_link(s):
        """s is a linked list if it is empty or a (first, rest) pair."""
        return s == empty or (len(s) == 2 and is_link(s[1]))

>>> def link(first, rest):
        """Construct a linked list from its first element and the rest."""
        assert is_link(rest), "rest must be a linked list."
        return [first, rest]

>>> def first(s):
        """Return the first element of a linked list s."""
        assert is_link(s), "first only applies to linked lists."
        assert s != empty, "empty linked list has no first element."
        return s[0]

>>> def rest(s):
        """Return the rest of the elements of a linked list s."""
        assert is_link(s), "rest only applies to linked lists."
        assert s != empty, "empty linked list has no rest."
        return s[1]

Ci-dessus, la fonction link est un constructeur, et les fonctions first et rest sont des sélecteurs pour une représentation de données abstraites des listes chaînées. La condition de comportement d'une liste chaînée est que, comme pour une paire, son constructeur et ses sélecteurs sont des fonctions inverses.

• Si une liste chaînée s a été construite à partir du premier élément f et de la liste chaînée r, alors l'appel first(s) retourne f, et l'appel rest(s) renvoie r.

Nous pouvons utiliser le constructeur et les sélecteurs pour manipuler les listes chaînées.

>>> four = link(1, link(2, link(3, link(4, empty))))
>>> first(four)
1
>>> rest(four)
[2, [3, [4, 'empty']]]

Notre implémentation de ce type de données abstraites utilise des paires qui sont des valeurs de type list à deux éléments. Il convient de noter que nous avons également pu construire des paires en utilisant des fonctions, et nous pouvons implémenter des listes chaînées à l'aide de toutes les paires, donc nous pourrions implémenter des listes chaînées en utilisant uniquement des fonctions.

Une liste chaînée peut stocker une séquence de valeurs dans l'ordre, mais nous n'avons pas encore montré qu'elle satisfait l'abstraction de la séquence. En utilisant la représentation abstraite des données que nous avons définie, nous pouvons instaurer les deux comportements qui caractérisent une séquence : la longueur et la sélection d'élément.

>>> def len_link(s):
        """Return the length of linked list s."""
        length = 0
        while s != empty:
            s, length = rest(s), length + 1
        return length

>>> def getitem_link(s, i):
        """Return the element at index i of linked list s."""
        while i > 0:
            s, i = rest(s), i - 1
        return first(s)

Maintenant, nous pouvons manipuler une liste chaînée comme une séquence utilisant ces fonctions. (Nous ne pouvons pas encore utiliser la fonction len intégrée, la syntaxe de sélection d'élément ni instruction for, mais nous serons bientôt en mesure de le faire.)

>>> len_link(four)
4
>>> getitem_link(four, 1)
2

La série de diagrammes d'environnement ci-dessous illustre le processus itératif par lequel getitem_link trouve l'élément 2 à l'indice 1 dans une liste chaînée. Ci-dessous, nous avons défini la liste chaînée four en utilisant les primitives Python pour simplifier les diagrammes. Ce choix de mise en œuvre enfreint une barrière d'abstraction, mais nous permet d'inspecter le processus de calcul plus facilement pour cet exemple.

1    def first(s):
2        return s[0]
3    def rest(s):
4        return s[1]
5    
6    def getitem_link(s, i):
7        while i > 0:
8            s, i = rest(s), i - 1
9        return first(s)
10    
11    four = [1, [2, [3, [4, 'empty']]]]
12    getitem_link(four, 1)

Au départ, la fonction getitem_link est appelée et crée un cadre local.

def first(s):
  return s[0]
def rest(s):
  return s[1]
    
def getitem_link(s, i):
  while i > 0:
    s, i = rest(s), i - 1
    return first(s)

four = [1, [2, [3, [4, 'empty']]]]
getitem_link(four, 1)

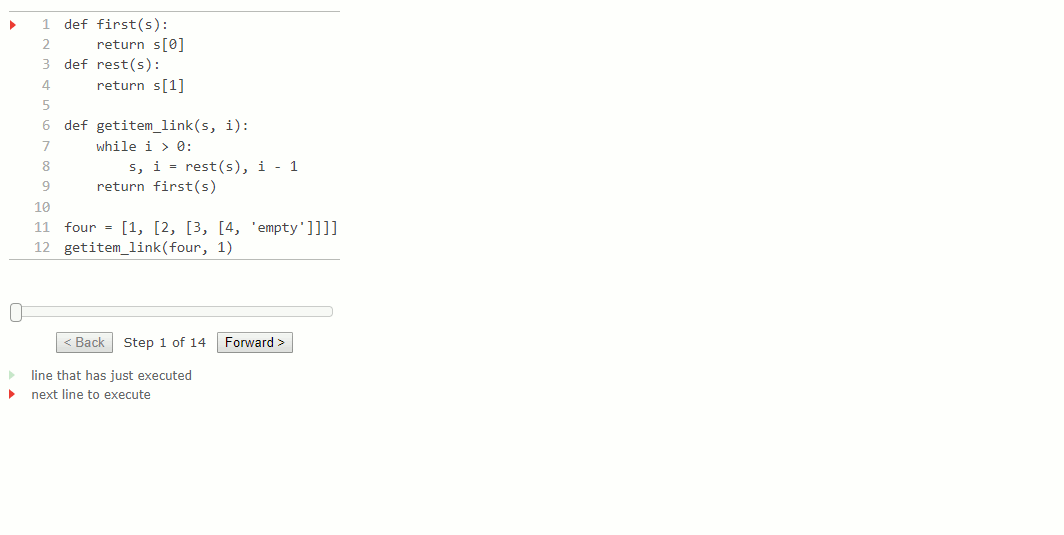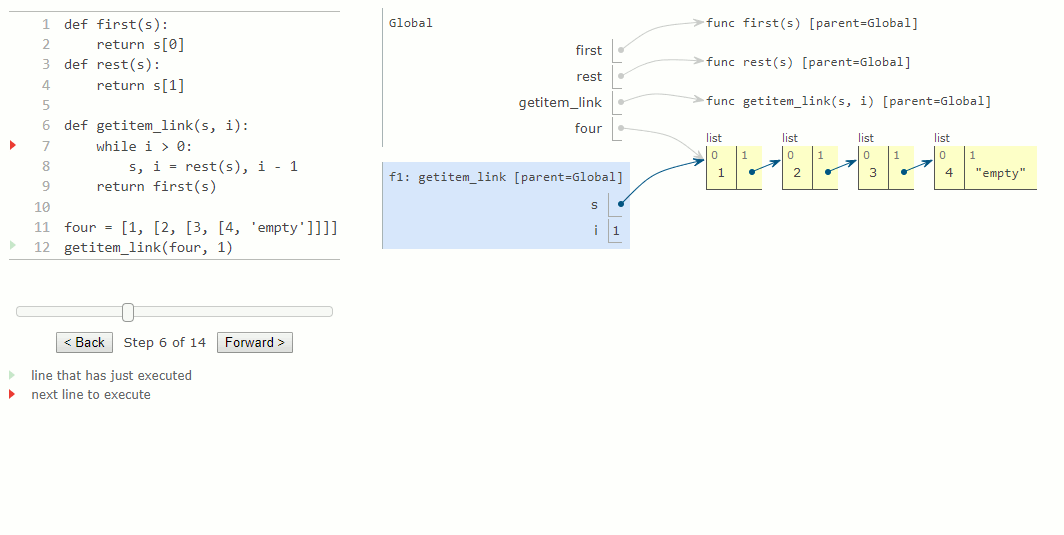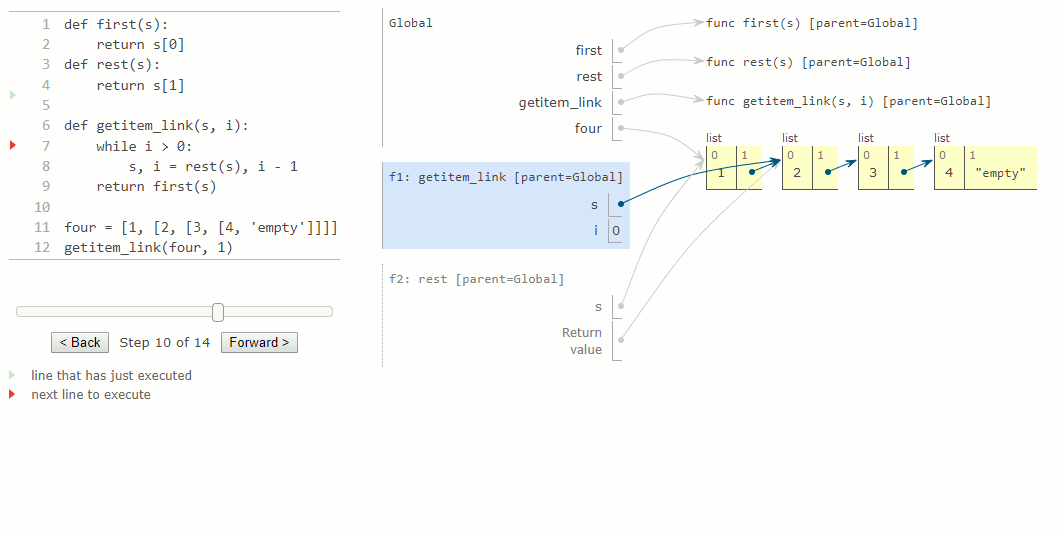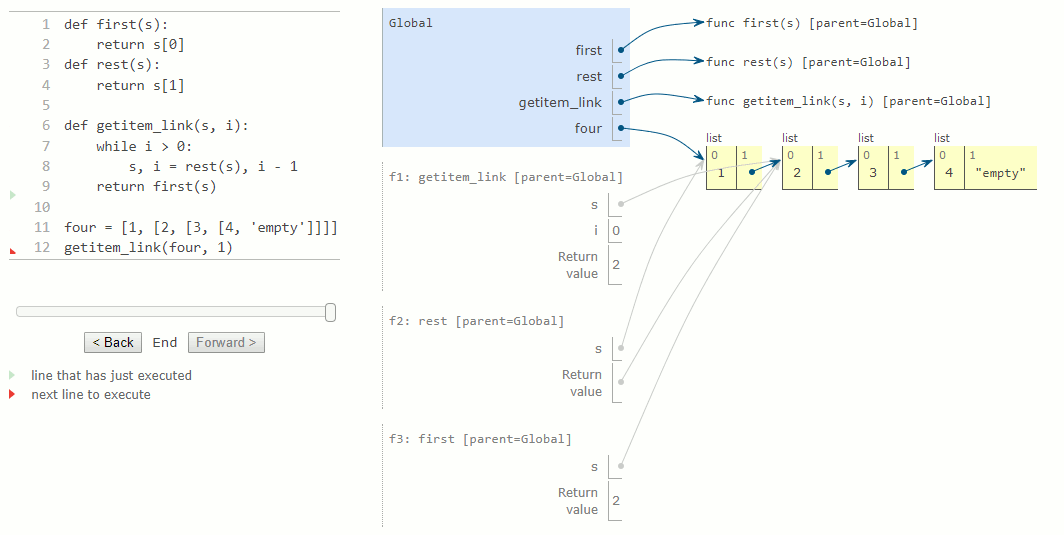
L'expression dans l'entête de l'instruction while s'évalue à True, ce qui entraîne l'exécution de l'instruction d'affectation dans le corps du while. La fonction rest renvoie la sous-liste à partir de 2.

def first(s):
  return s[0]
def rest(s):
  return s[1]
    
def getitem_link(s, i):
  while i > 0:
    s, i = rest(s), i - 1
    return first(s)

four = [1, [2, [3, [4, 'empty']]]]
getitem_link(four, 1)

Ensuite, le nom local s sera mis à jour pour désigner la sous-liste qui commence au deuxième élément de la liste d'origine. L'évaluation de l'expression dans l'en-tête de l'instruction while renvoie maintenant une valeur fausse, et Python sort de la boucle while et évalue l'expression dans l'instruction de retour de la dernière ligne de getitem_link.

def first(s):
  return s[0]
def rest(s):
  return s[1]

def getitem_link(s, i):
  while i > 0:
    s, i = rest(s), i - 1
    return first(s)

four = [1, [2, [3, [4, 'empty']]]]
getitem_link(four, 1)

Ce diagramme d'environnement final montre la trame locale pour l'appel de first, qui contient le nom s lié à cette même sous-liste. La fonction first sélectionne la valeur 2 et la renvoie ; cette valeur sera également retournée par getitem_link.

Cet exemple illustre un modèle commun de calcul avec des listes chaînées : chaque étape d'une itération traite un suffixe de plus en plus court de la liste d'origine. Ce traitement incrémental de recherche de la longueur et des éléments d'une liste chaînée prend du temps à calculer. Les types de séquence intégrés de Python sont implémentés d'une manière différente qui n'a pas ce coût élevé pour calculer la longueur d'une séquence ou récupérer de ses éléments. Les détails de cette représentation dépassent le périmètre de ce texte.

Manipulation récursive. Les fonctions liens len_link et getitem_link sont itératifs. Ils éliminent chaque couche de paire imbriquée jusqu'à la fin de la liste (dans len_link) ou jusqu'à ce que l'élément désiré (dans getitem_link) soit atteint. Nous pouvons également implémenter le calcul de la longueur et la sélection des éléments en utilisant la récursivité :

>>> def len_link_recursive(s):
        """Return the length of a linked list s."""
        if s == empty:
            return 0
        return 1 + len_link_recursive(rest(s))

>>> def getitem_link_recursive(s, i):
        """Return the element at index i of linked list s."""
        if i == 0:
            return first(s)
        return getitem_link_recursive(rest(s), i - 1)

>>> len_link_recursive(four)
4
>>> getitem_link_recursive(four, 1)
2

Ces implémentations récursives suivent la chaîne de paires jusqu'à la fin de la liste (en len_link_recursive) ou jusqu'à ce que l'élément recherché (en getitem_link_recursive) soit atteint.

La récursivité est également utile pour transformer et combiner des listes chaînées :

>>> def extend_link(s, t):
        """Return a list with the elements of s followed by those of t."""
        assert is_link(s) and is_link(t)
        if s == empty:
            return t
        else:
            return link(first(s), extend_link(rest(s), t))

>>> extend_link(four, four)
[1, [2, [3, [4, [1, [2, [3, [4, 'empty']]]]]]]]

>>> def apply_to_all_link(f, s):
        """Apply f to each element of s."""
        assert is_link(s)
        if s == empty:
            return s
        else:
            return link(f(first(s)), apply_to_all_link(f, rest(s)))

>>> apply_to_all_link(lambda x: x*x, four)
[1, [4, [9, [16, 'empty']]]]

>>> def keep_if_link(f, s):
        """Return a list with elements of s for which f(e) is true."""
        assert is_link(s)
        if s == empty:
            return s
        else:
            kept = keep_if_link(f, rest(s))
            if f(first(s)):
                return link(first(s), kept)
            else:
                return kept

>>> keep_if_link(lambda x: x%2 == 0, four)
[2, [4, 'empty']]

>>> def join_link(s, separator):
        """Return a string of all elements in s separated by separator."""
        if s == empty:
            return ""
        elif rest(s) == empty:
            return str(first(s))
        else:
            return str(first(s)) + separator + join_link(rest(s), separator)

>>> join_link(four, ", ")
'1, 2, 3, 4'

Construction récursive. Les listes chaînées sont particulièrement utiles lors de la construction progressive de séquences, une situation qui survient souvent dans les calculs récursifs.

La fonction count_partitions fonction du premier chapitre comptait le nombre de façons de partitionner un nombre entier n en utilisant des parties jusqu'à la taille m par l'intermédiaire d'un processus récursif sur un arbre. Avec des séquences, on peut également énumérer ces partitions explicitement en employant un processus similaire.

Nous suivons la même analyse récursive du problème que nous avons faite tout en comptant : Le partitionnement n utilisant des entiers jusqu'à m implique soit :

1. le partitionnement n-m en utilisant des nombres entiers allant jusqu'à m, soit
2. le partitionnement n en utilisant des nombres entiers allant jusqu'à m-1.

Pour les cas de base, nous constatons que 0 a une partition vide, et qu'il est impossible de partitionner un nombre entier négatif ou d'utiliser des parties plus petites que 1.

>>> def partitions(n, m):
        """Return a linked list of partitions of n using parts of up to m.
        Each partition is represented as a linked list.
        """
        if n == 0:
            return link(empty, empty) # A list containing the empty partition
        elif n < 0 or m == 0:
            return empty
        else:
            using_m = partitions(n-m, m)
            with_m = apply_to_all_link(lambda s: link(m, s), using_m)
            without_m = partitions(n, m-1)
            return extend_link(with_m, without_m)

Dans cette version récursive, on construit deux sous-listes de partitions. La première utilise m, donc on préfixe m à chaque élément du résultat using_m pour former with_m.

Le résultat de la fonction partitions est très imbriqué : une liste chaînée de listes chaînées, et chaque liste chaînée est représentée sous forme de paires imbriquées qui sont de type list. En utilisant join_link avec des séparateurs appropriés, on peut afficher les partitions d'une manière facile à lire pour un humain.

>>> def print_partitions(n, m):
        lists = partitions(n, m)
        strings = apply_to_all_link(lambda s: join_link(s, " + "), lists)
        print(join_link(strings, "\n"))

>>> print_partitions(6, 4)
4 + 2
4 + 1 + 1
3 + 3
3 + 2 + 1
3 + 1 + 1 + 1
2 + 2 + 2
2 + 2 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1