Composition de programmes

Au début de ce texte, nous avons distingué les fonctions et les données : les fonctions appliquent des opérations et les données sont ce sur quoi ces opérations sont appliquées. Lorsque nous avons inclus des fonctions parmi nos données, nous avons reconnu que les données peuvent également avoir un comportement. Les fonctions peuvent être manipulées en tant que données, mais peuvent également être appelées à effectuer des calculs.

Les objets combinent les valeurs de données à un comportement. Les objets représentent des informations, mais se comportent aussi comme les choses qu'ils représentent. La logique de la façon dont un objet interagit avec d'autres objets est regroupée avec les informations qui encodent la valeur de l'objet. Lorsqu'un objet est imprimé, il sait comment se représenter dans du texte. Si un objet est un assemblage de composants, il sait comment révéler ces composants à la demande. Les objets sont à la fois des informations et des processus, regroupés pour représenter les propriétés, les interactions et les comportements de choses complexes.

Le comportement de l'objet est implémenté en Python à travers une syntaxe d'objet spécialisée et une terminologie associée, que nous pouvons introduire avec un exemple. Une date est une sorte d'objet.

>>> from datetime import date

Le nom date est lié à une classe. Comme nous l'avons vu, une classe représente une sorte de valeur. Les dates individuelles sont appelées instances de cette classe. Les instances peuvent être construites en appelant la classe sur les arguments qui caractérisent l'instance.

>>> tues = date(2014, 5, 13)

L'objet tues (début du mot anglais signifiant mardi) a été construit à partir de nombres natifs, mais il se comporte comme une date. Par exemple, le soustraire d'une autre date donnera une différence de temps ou durée que nous pouvons imprimer.

>>> print(date(2014, 5, 19) - tues)
6 days, 0:00:00

Les objets ont des attributs, qui sont des valeurs nommées faisant partie de l'objet. En Python, comme dans beaucoup d'autres langages de programmation, nous utilisons une notation dite pointée pour désigner l'attribut d'un objet.

<expression> . <name>

Ci-dessus, <expression> s'évalue à un objet et <name> est le nom d'un attribut de cet objet.

Contrairement aux noms que nous avons considérés jusqu'ici, ces noms d'attributs ne sont pas disponibles dans l'environnement général. Au lieu de cela, les noms d'attributs sont particuliers à l'instance d'objet précédant le point.

>>> tues.year
2014

Les objets ont également des méthodes, qui sont des attributs dont la valeur est une fonction. Nous disons métaphoriquement que l'objet « sait » comment exécuter ces méthodes. Par construction, les méthodes sont des fonctions qui calculent leurs résultats à partir à la fois de leurs arguments et de l'objet qui les invoque. Par exemple, la méthode strftime (le nom d'une fonction classique censée renvoyer une chaîne de caractères représentant une date) de tues prend un seul argument qui spécifie comment afficher une date (par exemple, %A signifie que le jour de la semaine doit être inséré en entier dans la chaîne).

>>> tues.strftime('%A, %B %d')
'Tuesday, May 13'

Le calcul de la valeur de retour de strftime nécessite deux valeurs en entrée : la chaîne qui décrit le format de sortie et les informations relatives à la date regroupées en tues. Cette méthode applique une logique spécifique à la date pour générer ce résultat. Nous n'avons jamais spécifié que le 13 mai 2014 tombait un mardi, mais connaître le jour de semaine fait partie de ce que cela signifie d'être une date. En regroupant le comportement et l'information ensemble, cet objet Python nous offre une abstraction convaincante et autonome d'une date.

Les dates sont des objets, mais les nombres, les chaînes, les listes et les plages sont tous des objets. Non seulement ils représentent des valeurs, mais ils se comportent aussi de manière à respecter les valeurs qu'ils représentent. Ils ont également des attributs et des méthodes. Par exemple, les chaînes de caractères ont un ensemble de méthodes qui facilitent le traitement du texte.

>>> '1234'.isnumeric()
True
>>> 'rOBERT dE nIRO'.swapcase()
'Robert De Niro'
>>> 'eyes'.upper().endswith('YES')
True

En fait, toutes les valeurs de Python sont des objets. C'est-à-dire que toutes les valeurs ont un comportement et des attributs. Ils agissent comme les valeurs qu'ils représentent.

Les instances de valeurs intégrées primitives telles que les nombres sont immuables. Les valeurs elles-mêmes ne peuvent pas changer au cours de l'exécution du programme. Les listes, en revanche, sont mutables.

Les objets mutables sont utilisés pour représenter des valeurs qui changent avec le temps. Une personne est la même personne d'un jour à l'autre, si elle vieillit, subit une coupe de cheveux ou change d'une manière ou d'une autre. De même, un objet peut avoir des propriétés changeantes en raison des opérations de mutation. Par exemple, il est possible de modifier le contenu d'une liste. La plupart des modifications sont effectuées en invoquant des méthodes sur des objets de liste.

Nous pouvons présenter de nombreuses opérations de modification de listes avec un exemple qui illustre l'historique (radicalement simplifié) des cartes à jouer. Les commentaires dans les exemples décrivent l'effet de chaque appel de méthode.

Les cartes à jouer ont été inventées en Chine, peut-être vers le 9e siècle. Un des premiers jeux avait trois couleurs (en anglais, suits) correspondant à des dénominations d'argent.

>>> chinese = ['coin', 'string', 'myriad']  # Liste littérale
>>> suits = chinese             # Deux noms désignant la même liste

Quand les cartes ont migré vers l'Europe (en passant peut-être par l’Égypte), seule la couleur des pièces (coins) est resté dans les jeux de cartes espagnols (oro).

>>> suits.pop()             # Supprime et retourne l'élément final
'myriad'
>>> suits.remove('string')  # Supprimele premier élément égal à l'argument

Trois autres couleurs ont été ajoutées (leurs nom et apparence ont évolué au fil du temps) :

>>> suits.append('cup')              # Ajout d'un élément à la fin
>>> suits.extend(['sword', 'club'])  # Ajout de tous les éléments d'une séquence à la fin

Et les Italiens ont renommé les épées :

>>> suits[2] = 'spade'  # Remplace un élément

Ce qui donne les couleurs du jeu de cartes italien traditionnel :

>>> suits
['coin', 'cup', 'spade', 'club']

La variante française (dont les quatre couleurs sont pique, cœur, carreau et trèfle, soit dans le même ordre diamond, heart, spade et club en anglais), la plus communément utilisée aujourd'hui aux États-Unis et dans d'autres pays, modifie les deux premières couleurs :

>>> suits[0:2] = ['heart', 'diamond']  # Remplace une tranche
>>> suits
['heart', 'diamond', 'spade', 'club']

Des méthodes existent également pour l'insertion, le tri et l'inversion de listes. Toutes ces opérations de mutation modifient la valeur de la liste. Elles ne créent pas de nouveaux objets de liste.

Partage et identité. Comme nous avons changé une seule liste, et non créé de nouvelles listes, l'objet lié au nom chinois a également changé, car il s'agit du même objet-liste qui était lié à suits !

>>> chinese  # Comme "suits", ce nom correspond à la même liste modifiée
['heart', 'diamond', 'spade', 'club']

Ce comportement est nouveau. Jusqu'à présent, si un nom n'apparaissait pas dans une instruction, sa valeur ne pouvait pas être affectée par cette instruction. Avec les données mutables, les méthodes appelées sur un seul nom peuvent affecter un autre nom en même temps.

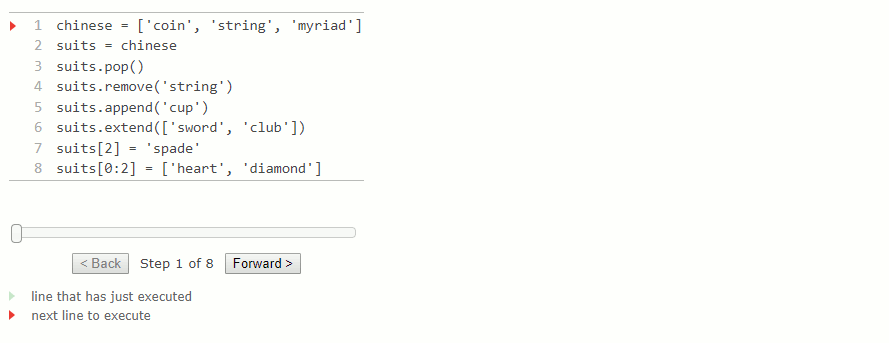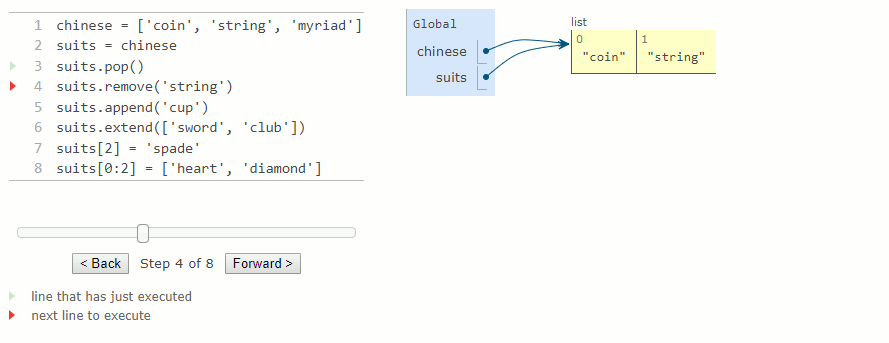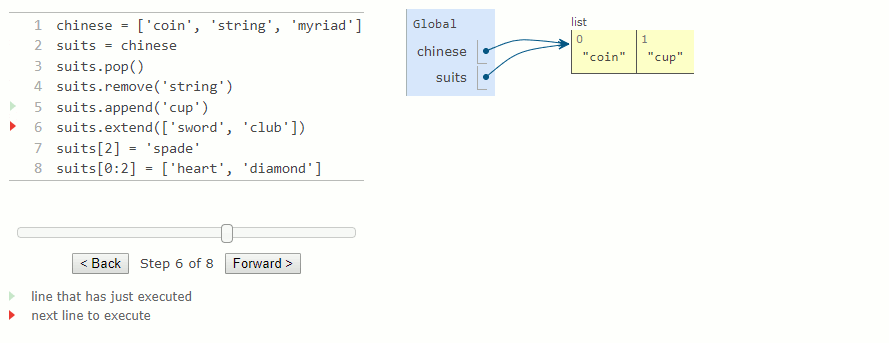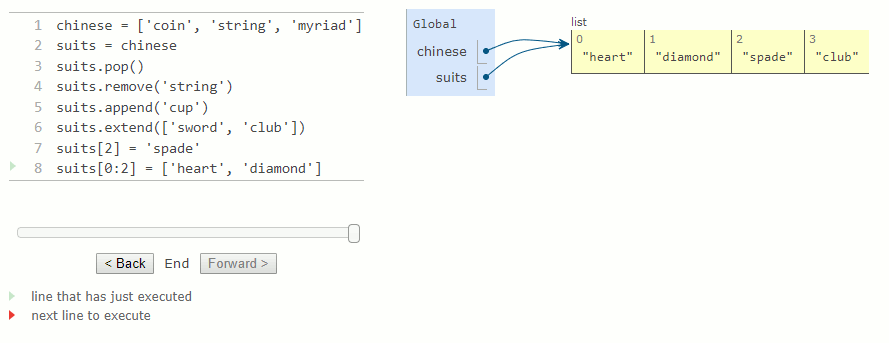
Le diagramme d'environnement pour cet exemple montre comment la valeur liée à chinese est modifiée par des instructions affectant uniquement des suits. Parcourez chaque ligne de l'exemple suivant pour observer ces modifications.

chinese = ['coin', 'string', 'myriad']
suits = chinese
suits.pop()
suits.remove('string')
suits.append('cup')
suits.extend(['sword', 'club'])
suits[2] = 'spade'
suits[0:2] = ['heart', 'diamond']

Les listes peuvent être copiées à l'aide du constructeur list. Dans ce cas, les modifications apportées à une liste n'affectent pas l'autre, à moins qu'elles ne partagent une structure commune.

>>> nest = list(suits)  # Liaison imbriquée à une seconde liste ayant les mêmes éléments
>>> nest[0] = suits     # Création d'une liste imbriquée

Dans cet environnement, changer la liste référencée par suits affectera la liste imbriquée qui est le premier élément de nest, mais pas les autres éléments.

>>> suits.insert(2, 'Joker')  # Insère un élément à l'indice 2 et décale le reste
>>> nest
[['heart', 'diamond', 'Joker', 'spade', 'club'], 'diamond', 'spade', 'club']

De même, défaire cette modification dans le premier élément de nest impactera également suits.

>>> nest[0].pop(2)
'Joker'
>>> suits
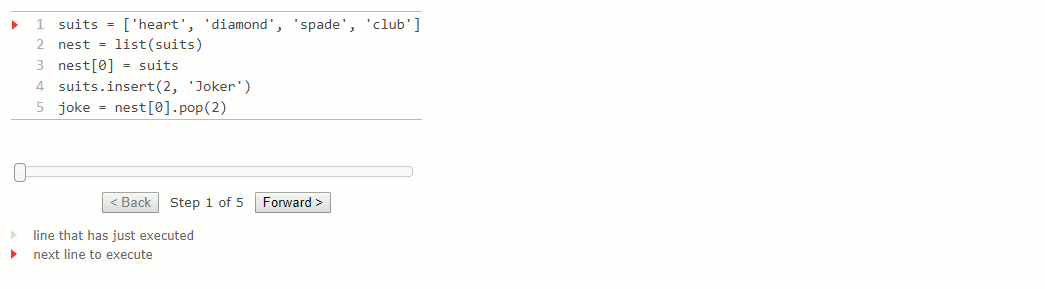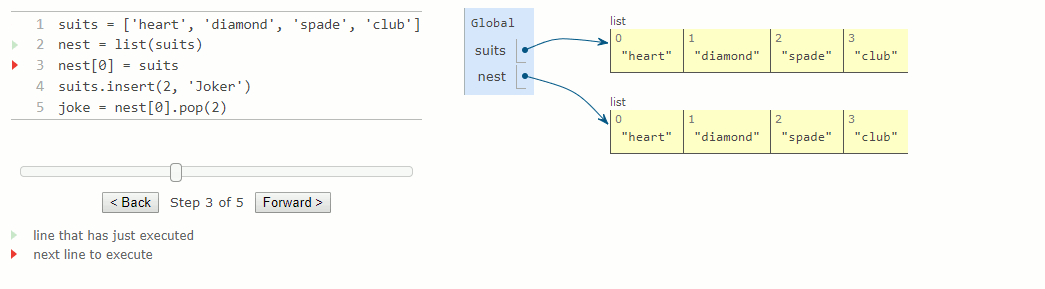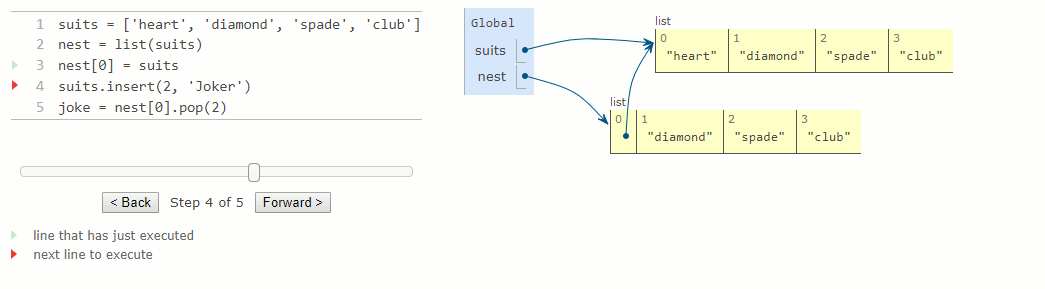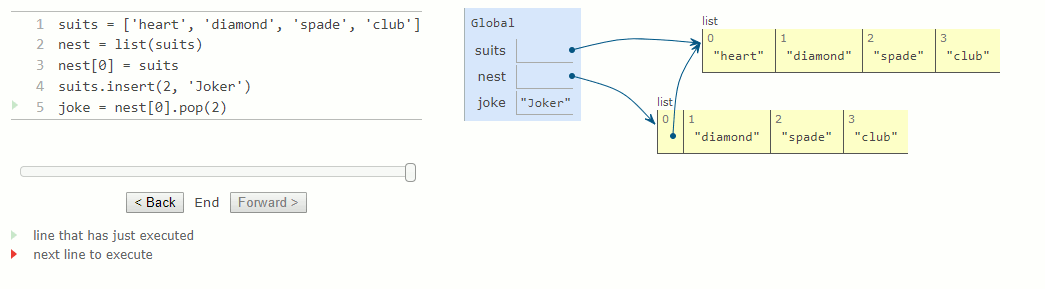
['heart', 'diamond', 'spade', 'club']

Exécuter cet exemple pas à pas révélera la représentation d'une liste imbriquée.

suits = ['heart', 'diamond', 'spade', 'club']
nest = list(suits)
nest[0] = suits
suits.insert(2, 'Joker')
joke = nest[0].pop(2)

Comme deux listes peuvent avoir le même contenu mais être en fait des listes différentes, nous avons besoin d'un moyen pour vérifier si deux objets sont identiques. Python fournit deux opérateurs de comparaison d'identité, appelés is et is not, qui testent si deux expressions renvoient le même objet. Deux objets sont identiques s'ils ont actuellement la même valeur et si tout changement à l'un sera toujours reflété dans l'autre. L'identité est une condition plus forte que l'égalité.

>>> suits is nest[0]
True
>>> suits is ['heart', 'diamond', 'spade', 'club']
False
>>> suits == ['heart', 'diamond', 'spade', 'club']
True

Les deux dernières comparaisons illustrent la différence entre les opérateurs is et ==. Le premier vérifie l'identité, tandis que le dernier vérifie l'égalité des contenus.

Manipulation de liste : le comportement des fonctions et des méthodes de listes peut être mieux compris en termes de mutation d'objet et d'identité. Les listes comportent un grand nombre de méthodes intégrées utiles dans de nombreux scénarios, et la compréhension de leur comportement est donc utile pour une meilleure productivité.

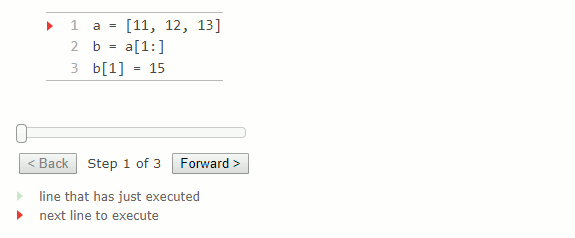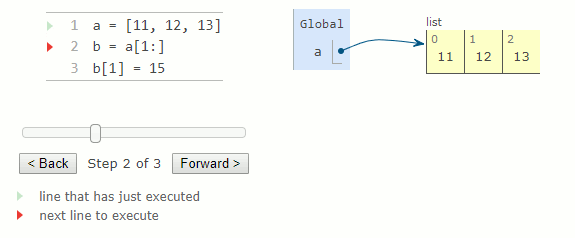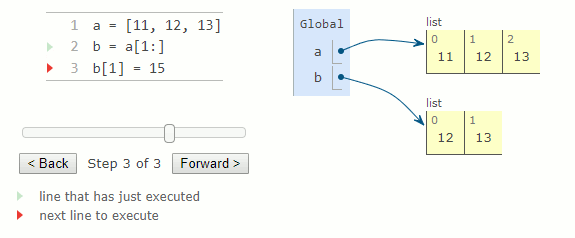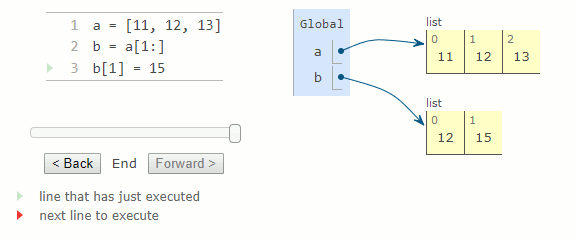
Extraire une tranche (slice) d'une liste crée une nouvelle liste et laisse la liste d'origine inchangée. Une tranche allant du début à la fin de la liste est un moyen de copier le contenu.

a = [11, 12, 13]
b = a [1:]
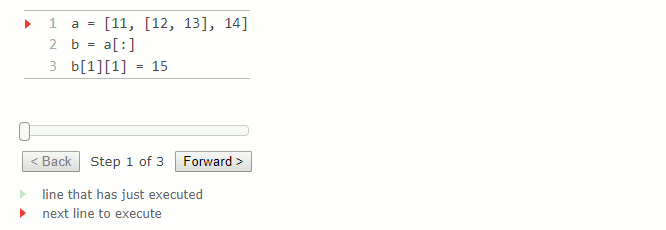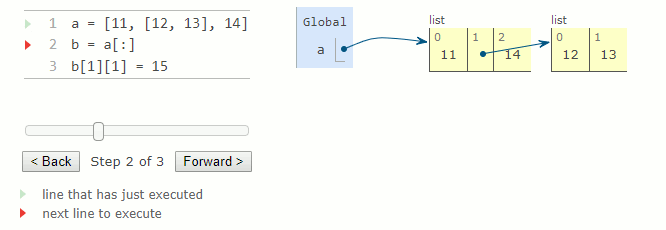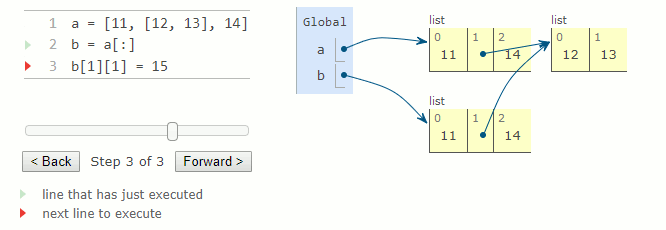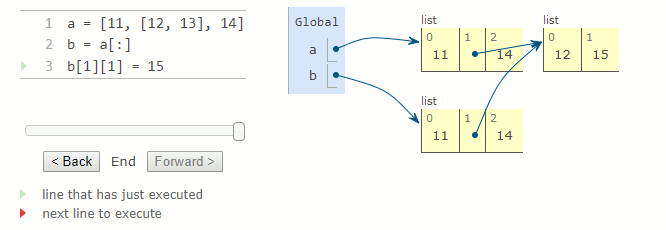
b[1] = 15

Bien que la liste soit copiée, les valeurs contenues dans la liste ne le sont pas. Au lieu de cela, une nouvelle liste est créée et contient un sous-ensemble avec les mêmes valeurs que la liste dont on a pris une tranche. Par conséquent, modifier la tranche d'une liste affectera la liste d'origine.

a = [11, [12, 13], 14]
b = a[:]
b[1][1] = 15  # a[1][1] vaut maintenant 15

La fonction intégrée list crée une nouvelle liste contenant les valeurs de son argument, qui doit être une valeur itérable telle qu'une séquence. Encore une fois, les valeurs placées dans cette liste ne sont pas copiées. list(s) et s[:] sont équivalents pour une liste s.

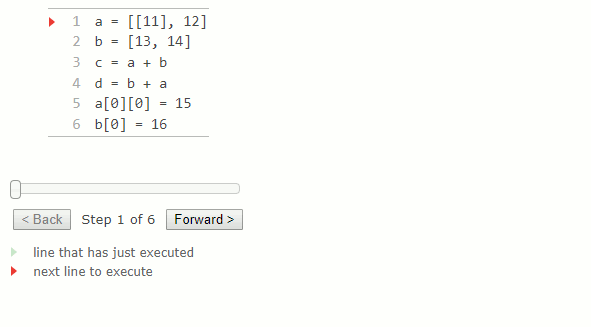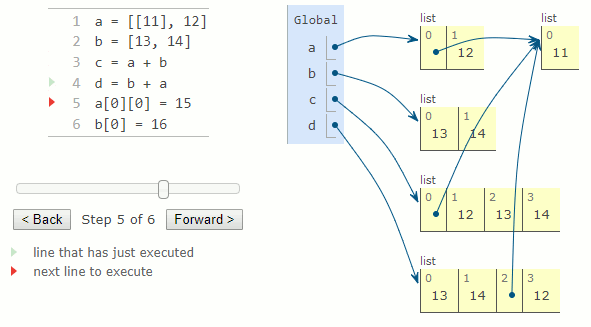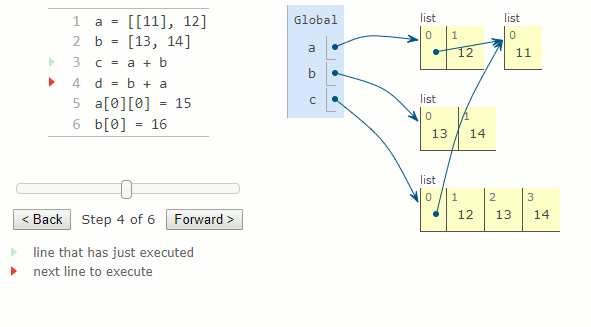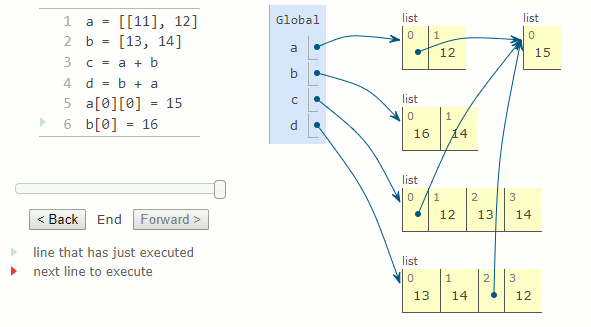
L'addition de deux listes crée une nouvelle liste contenant les valeurs de la première liste, suivie des valeurs de la deuxième liste. Par conséquent, a+b et b+a peuvent donner des valeurs différentes pour deux listes a et b. Cependant, l'opérateur += se comporte différemment pour les listes et son comportement est décrit ci-dessous avec la méthode extend.

a = [11], 12] 
b = [13, 14] 
c = a + b 
d = b + a 
a[0][0] = 15 
b[0] = 16

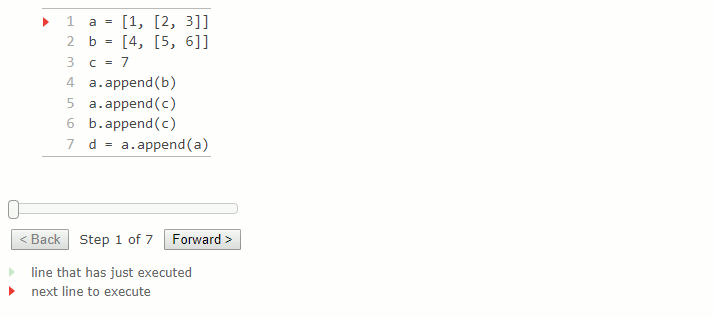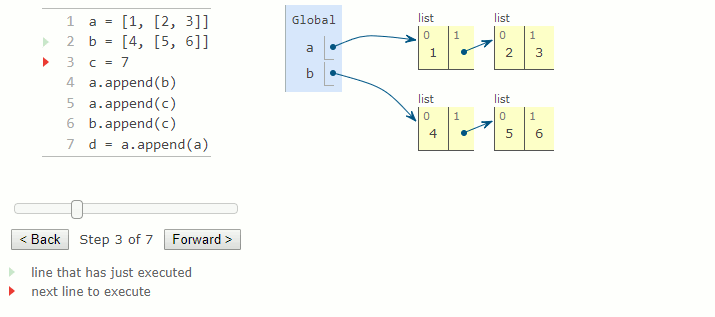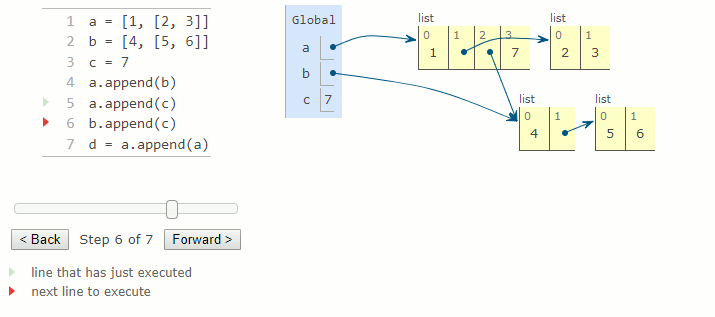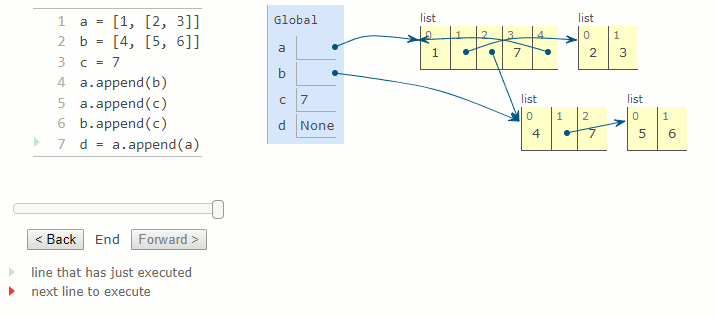
La méthode append d'une liste prend une valeur en argument et l'ajoute à la fin de la liste. L'argument peut être n'importe quelle valeur, soit un nombre, soit une autre liste. Si l'argument est une liste, cette liste (et non une copie) est ajoutée en tant qu'élément dans la liste. La méthode retourne toujours None et modifie la liste en augmentant sa longueur de un.

a = [1, [2, 3]] 
b = [4,[5, 6]] 
c = 7 
a.append(b) 
a.append(c) 
b.append(c) 
d = a.append(a)

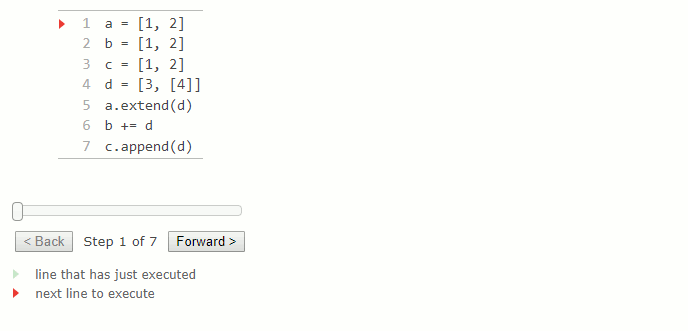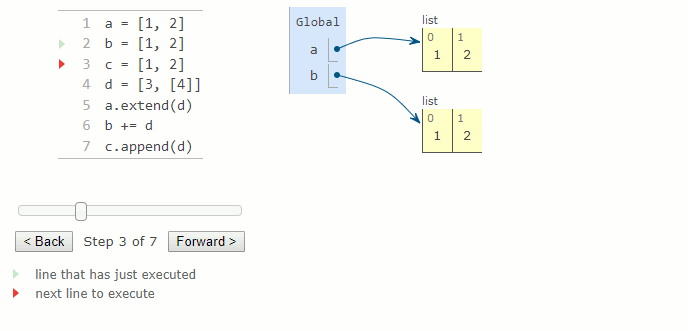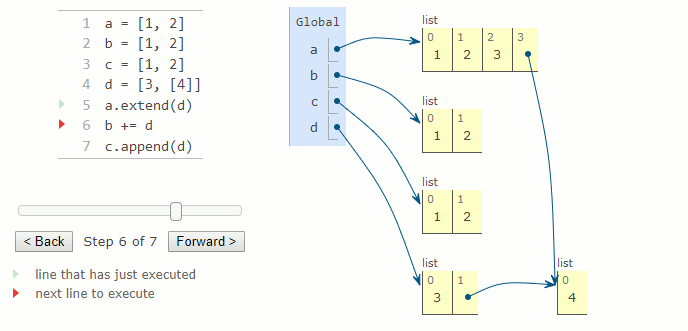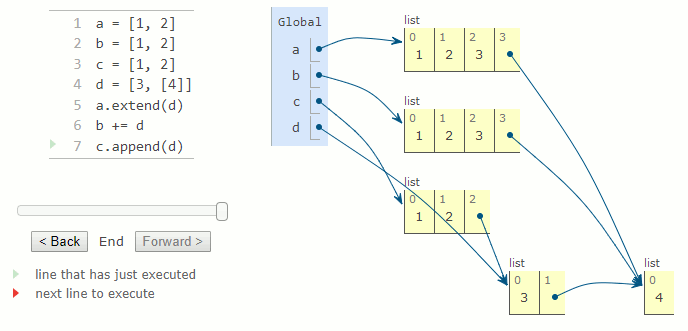
La méthode extend d'une liste prend une valeur itérable en argument et ajoute chacun de ses éléments à la fin de la liste. Elle change la liste en augmentant sa longueur de la longueur de l'argument itérable. L'instruction x += y pour une liste x et une valeur itérable y est équivalente à x.extend(y), à part quelques différences mineures qui ne sont pas abordées ici. Passer à extend un argument qui n'est pas itérable provoquera une erreur TypeError. La méthode ne retourne rien et elle modifie la liste.

a = [1, 2] 
b = [1, 2] 
c = [1, 2] 
d = [3, [4]] 
a.extend(d) 
b += d 
c.append(d)

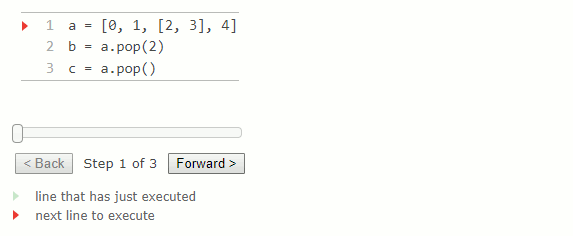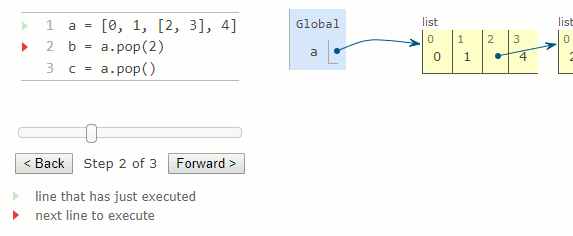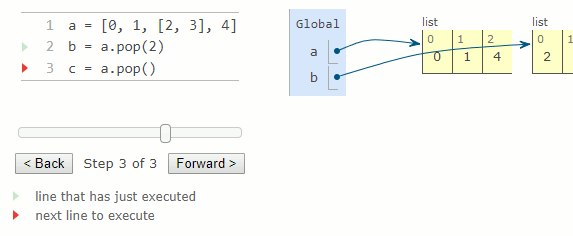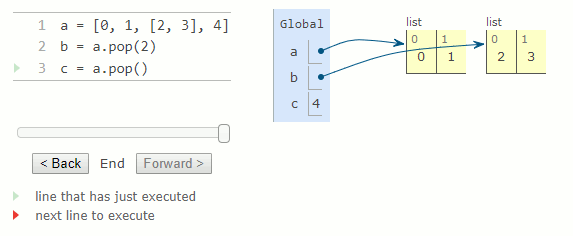
La méthode pop supprime et retourne le dernier élément de la liste. Lorsqu'il reçoit un argument entier i, il supprime et retourne l'élément à l'indice i de la liste. Cette méthode modifie la liste en réduisant sa longueur de un. Exécuter la méthode pop sur une liste vide provoque une erreur IndexError.

a = [0, 1, [2, 3], 4] 
b = a.pop(2) 
c = a.pop()

La méthode remove prend un argument qui doit être égal à une valeur dans la liste. Il supprime le premier élément de la liste correspondant à son argument. L'appel de remove avec une valeur ne correspondant à aucune valeur de la liste entraîne une erreur ValueError.

a = [10, 11, 10, 12, [13, 14]] 
a.remove([13, 14]) 
a.remove(10)

La méthode index prend un argument qui doit être égal à une valeur dans la liste. Il renvoie l'indice du premier élément égal à l'argument dans la liste. L'appel de index avec une valeur ne correspondant à aucun élément de la liste provoque une erreur ValueError.

>>> a = [13, 14, 13, 12, [13, 14], 15]
>>> a.index([13, 14])
4
>>> a.index(13)
0

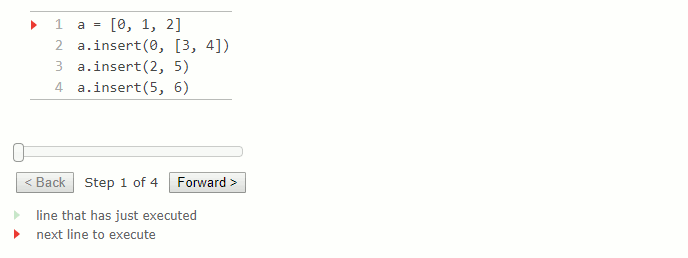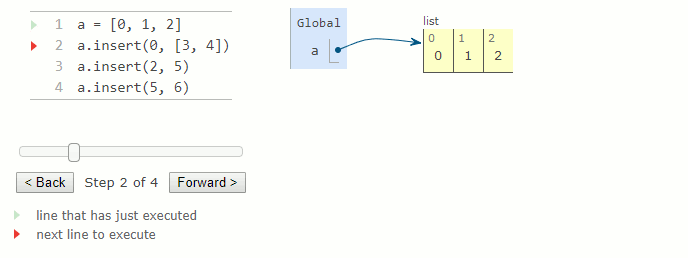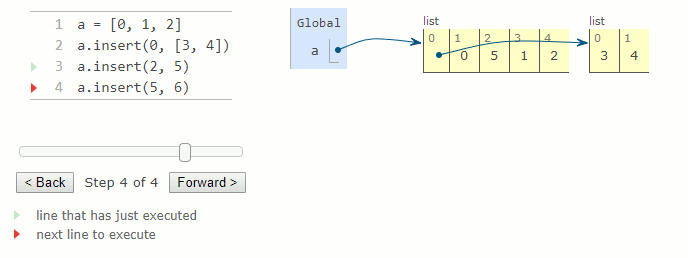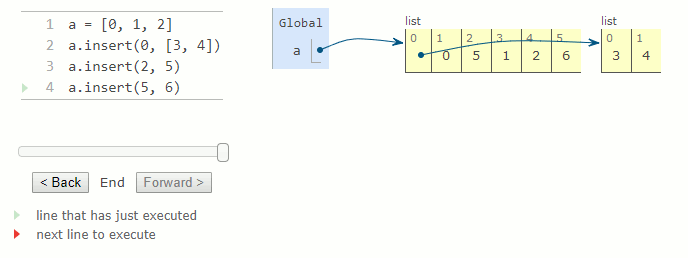
La méthode insert prend deux arguments : un indice et une valeur à insérer. La valeur est ajoutée à la liste à l'emplacement correspondant à l'indice donné. Tous les éléments avant l'indice spécifié restent les mêmes, mais tous les éléments après l'indice ont leurs indices augmentés de un. Cette méthode modifie la liste en augmentant sa taille de un, puis retourne None.

a = [0, 1, 2] 
a.insert(0, [3, 4]) 
a.insert(2, 5) 
a.insert(5, 6)

La méthode count d'une liste prend un élément en argument et renvoie le nombre de fois où cet élément apparaît dans la liste. Si l'argument n'est égal à aucun élément de la liste, alors count renvoie 0.

>>> a = [1, [2, 3], 1, [4, 5]]
>>> a.count([2, 3])
1
>>> a.count(1)
2
>>> a.count(5)
0

Listes en compréhension. Une liste en compréhension crée toujours une nouvelle liste. Par exemple, le module unicodedata stocke les noms officiels de chaque caractère dans l'alphabet Unicode. Nous pouvons rechercher les caractères correspondant aux noms, y compris ceux des couleurs de cartes.

>>> from unicodedata import lookup
>>> [lookup('WHITE ' + s.upper() + ' SUIT') for s in suits]
['♡', '♢', '♤', '♧']

Cette liste résultante ne partage pas son contenu avec suits, et l'évaluation de la liste en compréhension ne modifie pas la liste suits.

Tuples. Un tuple, une instance du type tuple intégré, est une séquence immuable. Les tuples sont créés en utilisant un tuple littéral qui sépare les expressions des éléments par des virgules. Les parenthèses sont facultatives mais utilisées couramment dans la pratique. On peut stocker toutes sortes d'objets dans des tuples.

>>> 1, 2 + 3
(1, 5)
>>> ("the", 1, ("and", "only"))
('the', 1, ('and', 'only'))
>>> type( (10, 20) )
<class 'tuple'>

Les tuples vides et à un seul élément ont une syntaxe littérale spéciale :

>>> ()    # 0 elements
()
>>> (10,) # 1 element
(10,)

Comme les listes, les tuples ont une longueur finie et autorisent la sélection d'éléments. Ils ont également quelques méthodes qui sont également disponibles pour les listes, comme count et index :

>>> code = ("up", "up", "down", "down") + ("left", "right") * 2
>>> len(code)
8
>>> code[3]
'down'
>>> code.count("down")
2
>>> code.index("left")
4

Cependant, les méthodes de manipulation du contenu d'une liste ne sont pas disponibles pour les tuples puisque les tuples sont immuables.

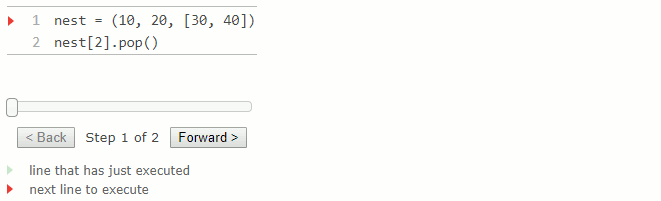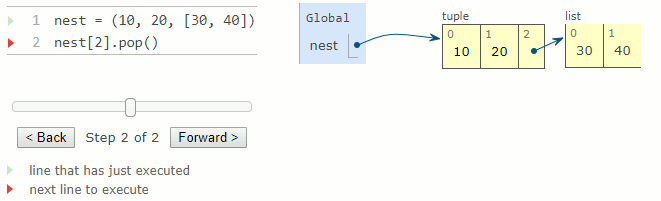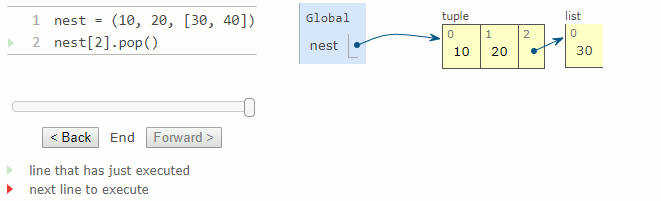
Bien qu'il soit impossible de modifier les éléments d'un tuple, il est possible de modifier la valeur d'un élément mutable contenu dans un tuple.

nest = (10, 20, [30, 40])
nest[2].pop()

Les tuples sont utilisés implicitement dans les affectations multiples. Une affectation de deux valeurs à deux noms crée un tuple à deux éléments puis dépaquette les éléments.

Les dictionnaires sont le type de données intégré de Python pour stocker et manipuler les relations de correspondance. Un dictionnaire contient des paires clef-valeur, dans lesquelles les clefs et les valeurs sont des objets. Le but d'un dictionnaire est de fournir une abstraction pour stocker et récupérer des valeurs qui sont indexées non par des entiers consécutifs, mais par des clefs descriptives.

Les clefs sont souvent des chaînes de caractères, car les chaînes sont notre représentation conventionnelle des noms de choses. Ce dictionnaire littéral donne les valeurs de différents chiffres romains.

>>> numerals = {'I': 1.0, 'V': 5, 'X': 10}

La recherche de valeurs par leurs clefs utilise l'opérateur de sélection d'élément que nous avons précédemment employé pour des séquences :

>>> numerals['X']
10

Un dictionnaire peut avoir au plus une valeur pour chaque clef. L'ajout de nouvelles paires de clefs-valeurs et la modification de la valeur existante d'une clé peuvent s'effectuer par des instructions d'affectation :

>>> numerals['I'] = 1
>>> numerals['L'] = 50
>>> numerals
{'I': 1, 'X': 10, 'L': 50, 'V': 5}

Notez que 'L' n'a pas été ajouté à la fin de la sortie ci-dessus (mais avant). Les dictionnaires sont des collections non ordonnées de paires clef-valeur. Lorsque nous imprimons un dictionnaire, les clés et les valeurs sont rendues dans un certain ordre, mais en tant qu'utilisateurs du langage, nous ne pouvons pas prédire ce que sera cet ordre. L'ordre peut changer si nous lançons plusieurs fois le même programme.

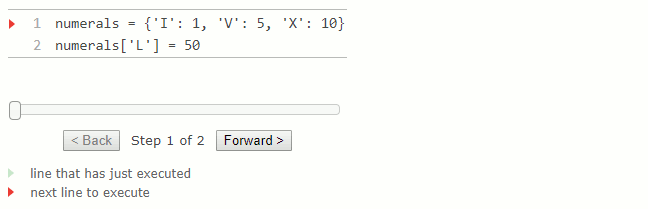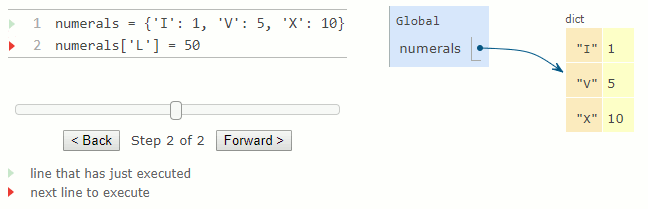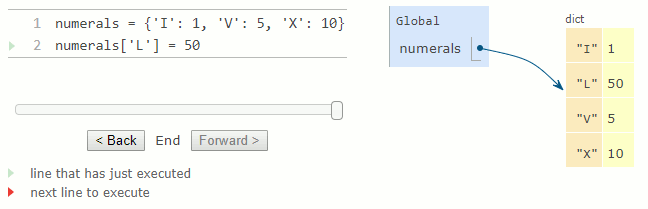
Les dictionnaires peuvent également apparaître dans des diagrammes d'environnement.

numerals = {'I': 1, 'V': 5, 'X': 10}
numerals['L'] = 50

Le type Dictionary prend également en charge diverses méthodes d'itération sur le contenu du dictionnaire dans son ensemble. Les méthodes keys, values et items renvoient toutes les valeurs itérables.

>>> sum(numerals.values())
66

Une liste de paires clé-valeur peut être convertie en un dictionnaire en appelant la fonction constructeur dict.

>>> dict([(3, 9), (4, 16), (5, 25)])
{3: 9, 4: 16, 5: 25}

Les dictionnaires ont certaines restrictions :

• Une clé d'un dictionnaire ne peut pas être ou contenir une valeur mutable.
• Il peut y avoir au plus une valeur pour une clé donnée.

Cette première restriction est liée à la mise en œuvre sous-jacente des dictionnaires dans Python. Ce texte ne couvrira pas les détails de cette implémentation. Intuitivement, considérez que la clé indique à Python où trouver cette paire clé-valeur dans la mémoire ; si la clé change, l'emplacement de la paire peut être perdu. On utilise assez couramment des tuples comme clés dans les dictionnaires, parce que les listes (qui sont mutables) ne peuvent pas servir de clés.

La deuxième restriction est une conséquence de l'abstraction du dictionnaire, qui est conçu pour stocker et récupérer des valeurs pour les clés. Nous ne pouvons que récupérer la valeur d'une clé que s'il existe au plus une seule valeur pour cette clé dans le dictionnaire.

Les dictionnaires offrent une méthode utile, get, qui renvoie soit la valeur correspondant à la clé, si la clé est présente, soit une valeur par défaut. Les arguments de get sont la clé et la valeur par défaut.

>>> numerals = {'I': 1, 'V': 5, 'X': 10}
>>> numerals.get('A', 0)
0
>>> numerals.get('V', 0)
5

Les dictionnaires ont également une syntaxe de compréhension analogue à celle des listes. Une expression de clé et une expression de valeur sont séparées par deux points. L'évaluation d'un dictionnaire en compréhension crée un nouvel objet de type dictionnaire.

>>> {x: x*x for x in range(3,6)}
{3: 9, 4: 16, 5: 25}

Les listes et les dictionnaires ont un état local : ce sont des valeurs changeantes qui ont des contenus particuliers à un moment quelconque de l'exécution d'un programme. Le mot « état » implique un processus évolutif dans lequel cet état peut changer.

Les fonctions peuvent également avoir un état local. Par exemple, définissons une fonction qui modélise le processus de retrait d'argent d'un compte bancaire. Nous allons créer une fonction de retrait appelée withdraw, qui prend comme argument un montant à retirer. S'il y a suffisamment d'argent dans le compte pour couvrir le retrait, withdraw renverra le solde du compte après le retrait. Sinon, withdraw renverra le message « Insufficient funds ». Par exemple, si nous démarrons avec un crédit de 100 € sur le compte, nous souhaitons obtenir la séquence suivante de valeurs de retour en appelant withdraw :

>>> withdraw(25)
75
>>> withdraw(25)
50
>>> withdraw(60)
'Insufficient funds'
>>> withdraw(15)
35

Ci-dessus, l'expression withdraw(25), évaluée à deux reprises, renvoie des valeurs différentes. Ainsi, cette fonction définie par l'utilisateur n'est pas pure. L'appel de la fonction renvoie non seulement une valeur, mais a aussi pour effet secondaire de modifier en un certain sens la fonction, de sorte que l'appel suivant avec le même argument renvoie un résultat différent. Cet effet secondaire résulte du fait que withdraw modifie une liaison nom-valeur externe au cadre courant.

Pour que la fonction withdraw ait un sens, il faut qu'elle soit créée avec un solde de compte initial. La fonction make_withdraw est une fonction d'ordre supérieur qui prend un solde de départ comme argument. La fonction de withdraw est sa valeur de retour :

>>> withdraw = make_withdraw(100)

Une implémentation de make_withdraw nécessite un nouveau type d'instruction : une instruction nonlocal. Lorsque nous appelons make_withdraw, nous lions le nom balance (solde) au nom du montant initial. Nous définissons et renvoyons une fonction locale, withdraw, qui met à jour et renvoie la valeur de balance lorsqu'elle est appelée.

>>> def make_withdraw(balance):
        """Return a withdraw function that draws down balance with each call."""
        def withdraw(amount):
            nonlocal balance             # Declare the name "balance" nonlocal
            if amount > balance:
                return 'Insufficient funds'
            balance = balance - amount   # Re-bind the existing balance name
            return balance
        return withdraw

La déclaration nonlocal indique que chaque fois que nous modifions la liaison du nom balance, cette liaison est modifiée dans le premier cadre dans lequel balance est déjà lié. Rappelons que, sans l'instruction nonlocal, une instruction d'affectation lierait toujours un nom dans le premier cadre de l'environnement courant. L'instruction nonlocal indique que le nom apparaît quelque part dans l'environnement ailleurs que dans le premier cadre (local) ou dans le dernier cadre (global).

Les diagrammes d'environnement suivants illustrent les effets de plusieurs appels vers une fonction créée par make_withdraw.

def make_withdraw(balance):
  def withdraw(amount):
    nonlocal balance
    if amount > balance:
      return 'Insufficient funds'
    balance = balance - amount
    return balance
  return withdraw
    
wd = make_withdraw(20)
wd(5)
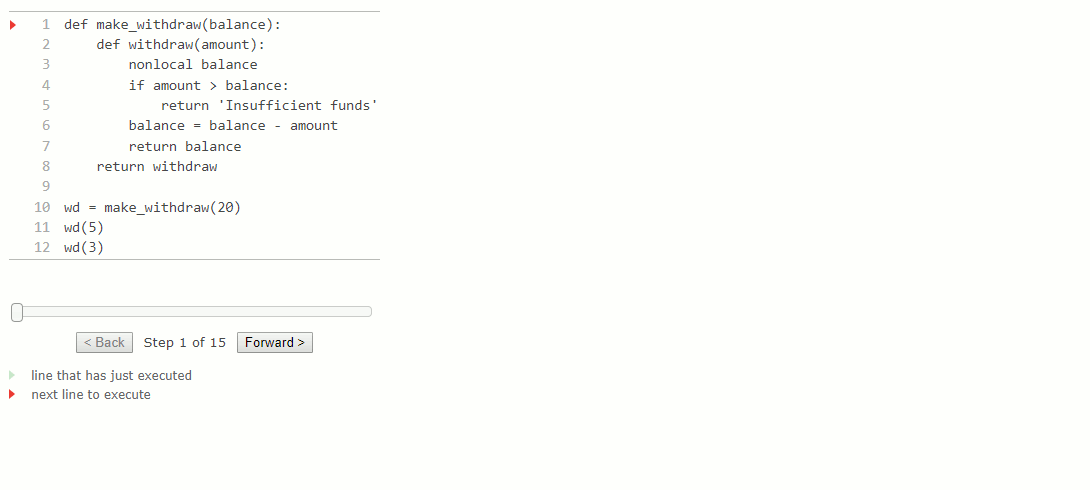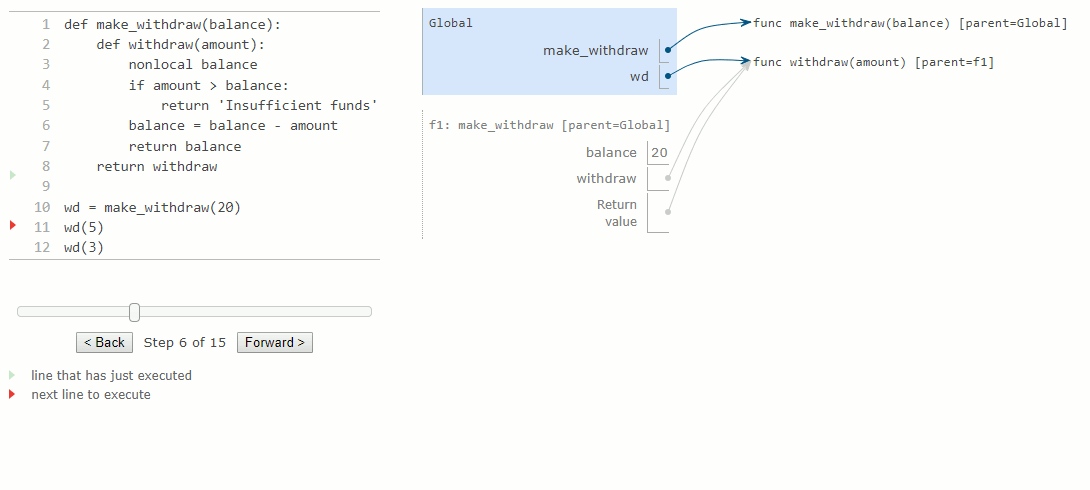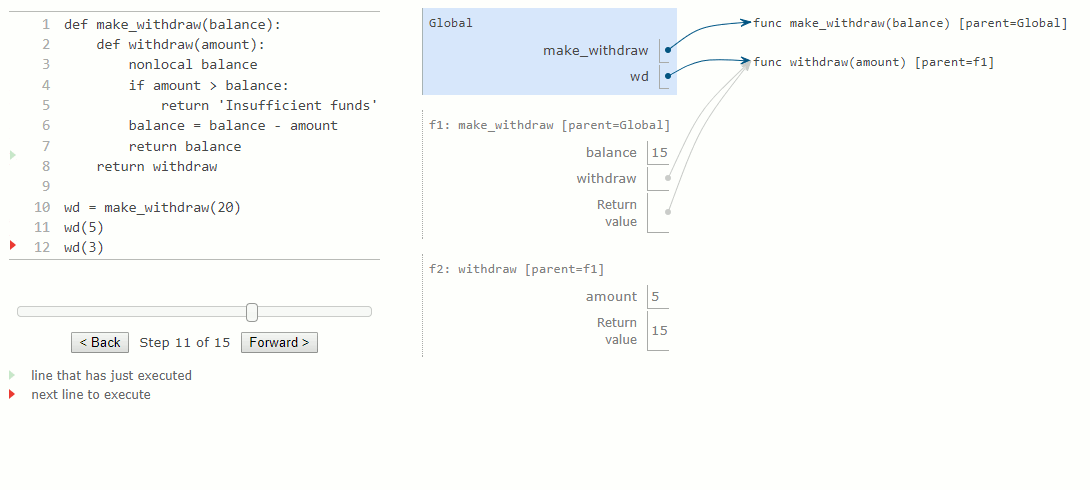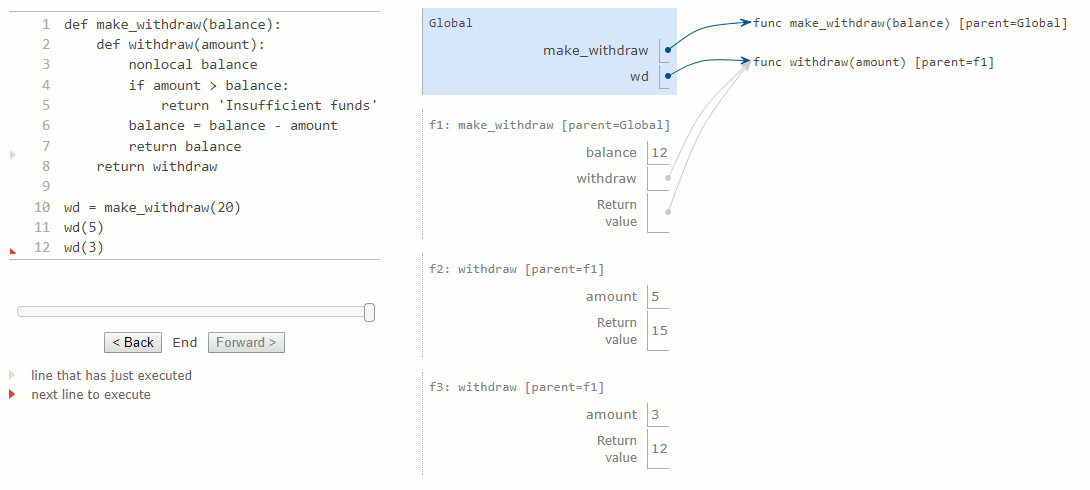
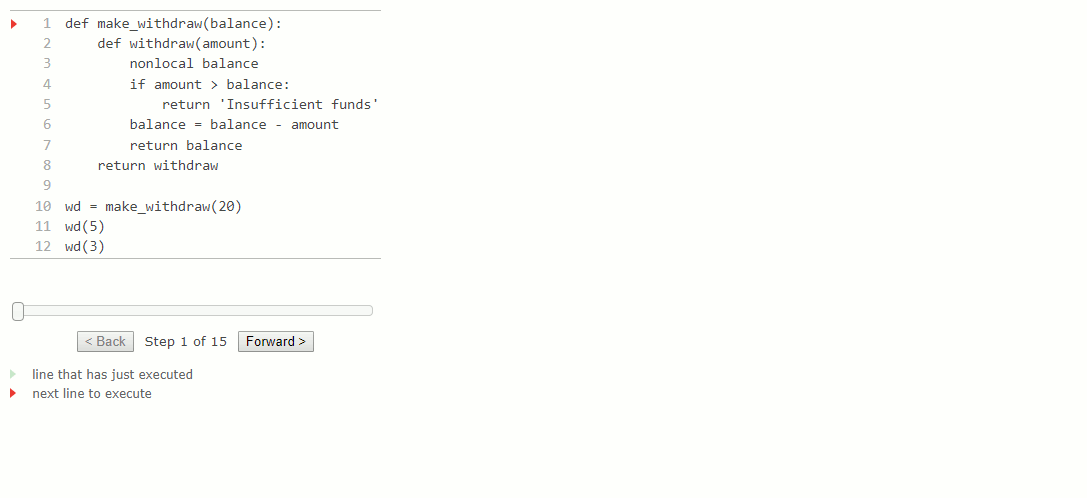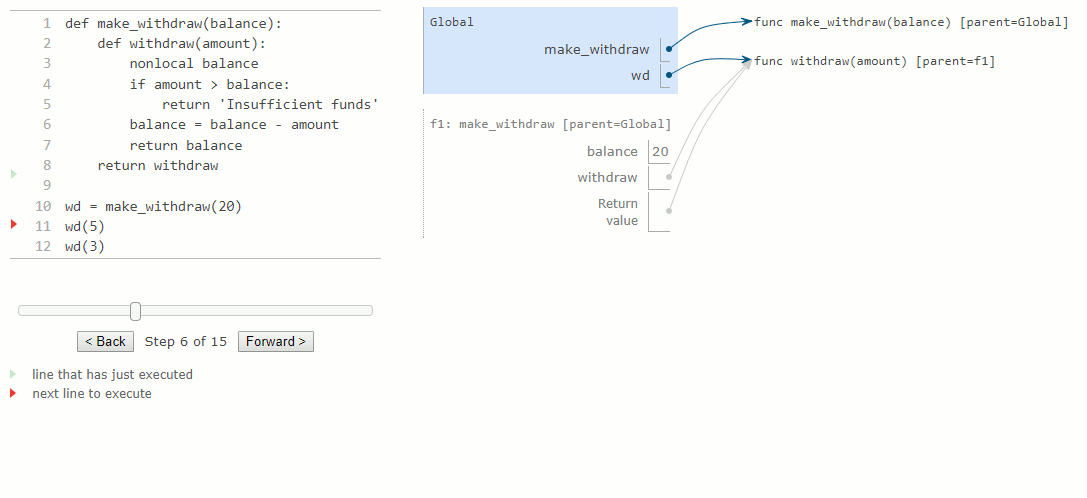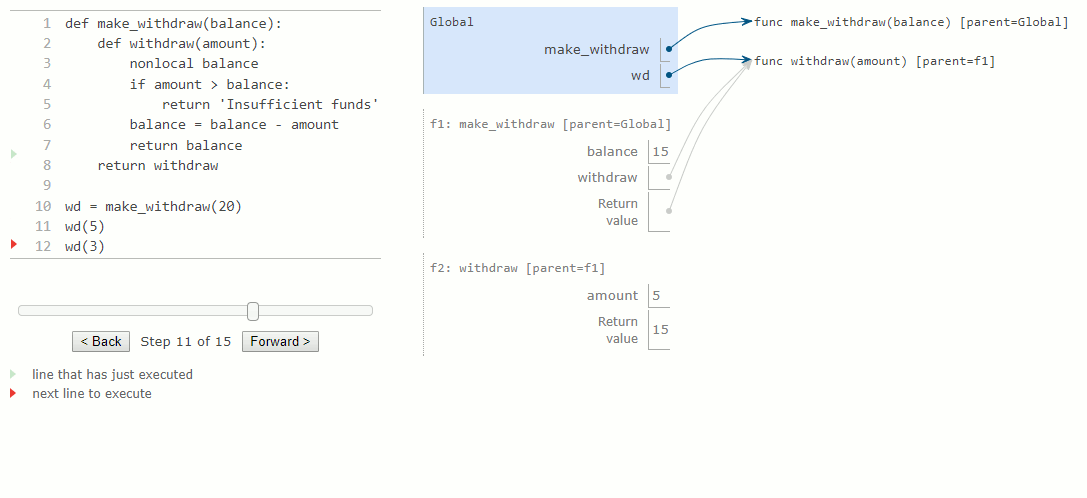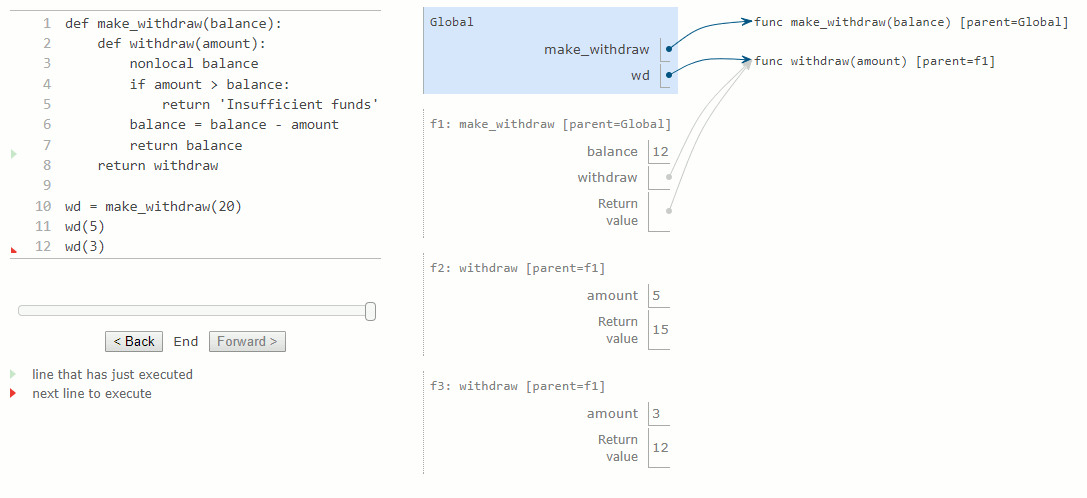
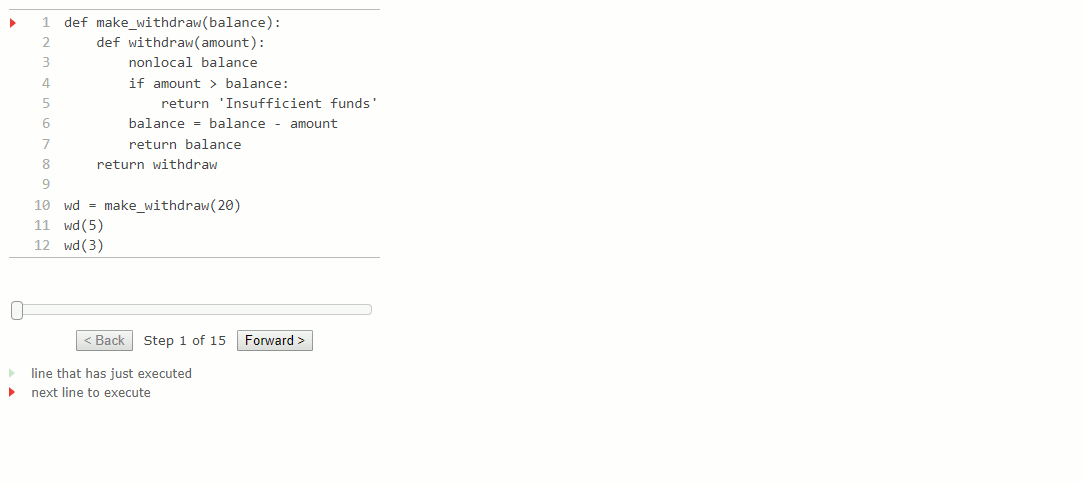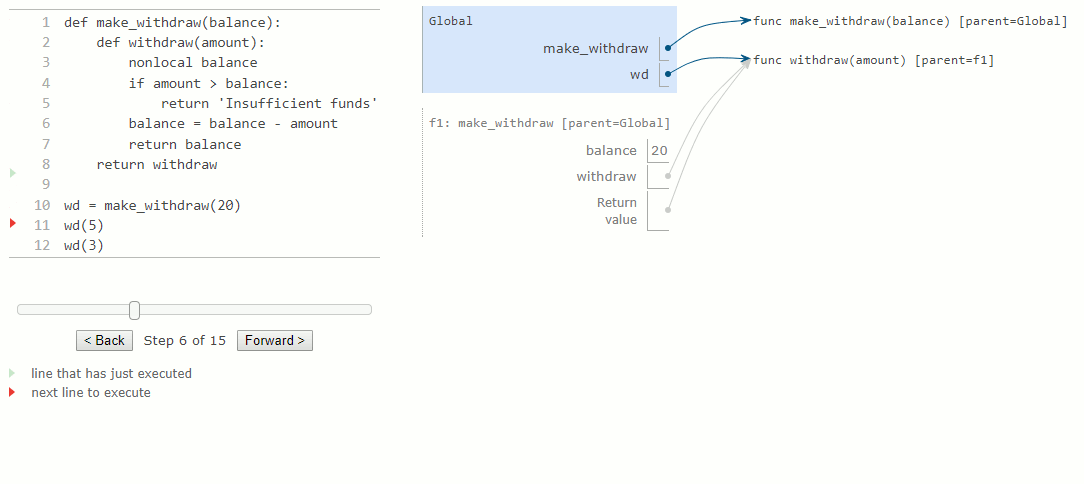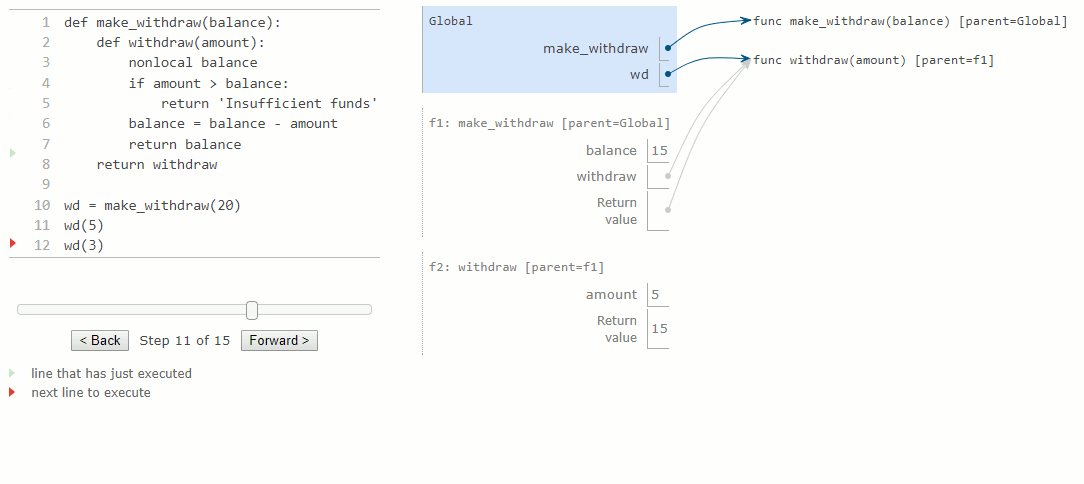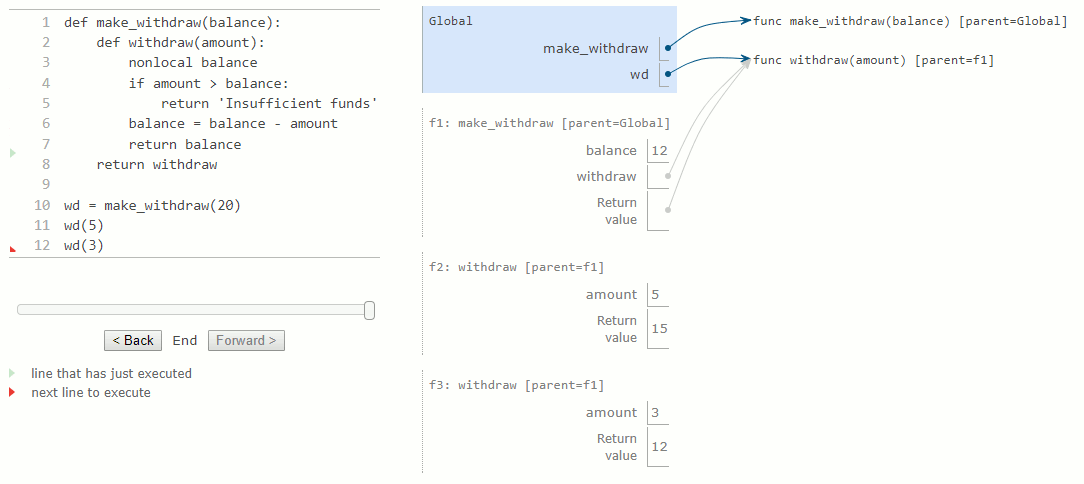
wd(3)

La première instruction def a l'effet habituel : elle crée une nouvelle fonction définie par l'utilisateur et lie le nom make_withdraw à cette fonction dans le cadre global. L'appel à make_withdraw plus bas crée et renvoie une fonction définie localement, withdraw. Le nom balance est lié au cadre parent de cette fonction. Il est essentiel de remarquer qu'il n'y aura que cette liaison unique pour le nom balance dans le reste de cet exemple.

Ensuite, nous évaluons une expression qui appelle cette fonction et la lie au nom wd, pour un montant de 5. Le corps de withdraw est exécuté dans un nouvel environnement qui étend l'environnement dans lequel la fonction withdraw a été définie. En traçant l'effet de l'évaluation du withdraw, on constate l'effet d'une déclaration nonlocal en Python : un nom en dehors du premier cadre local peut être modifié par une instruction d'affectation.

def make_withdraw(balance):
  def withdraw(amount):
    nonlocal balance
    if amount > balance:
      return 'Insufficient funds'
    balance = balance - amount
    return balance
  return withdraw

wd = make_withdraw(20)
wd(5)
wd(3)

La déclaration nonlocal modifie toutes les autres instructions d'affectation dans la définition de withdraw. Après avoir exécuté une déclaration nonlocal balance, toute instruction d'affectation avec balance à gauche du signe = ne liera pas balance dans le premier cadre de l'environnement actuel. Au lieu de cela, l'affectation trouvera le premier cadre dans lequel balance a déjà été défini et reliera le nom dans ce cadre. Si le nom balance n'était pas déjà lié à une valeur, l'instruction nonlocal produirait une erreur.

En raison de la modification de la liaison pour balance, nous avons également changé la fonction withdraw. La prochaine fois qu'on appellera cette fonction, le nom balance sera évalué à 15 au lieu de 20. Par conséquent, lorsque nous appelons withdraw une deuxième fois avec la valeur 3, nous voyons que sa valeur de retour est de 12 et non pas 17. La modification de balance lors du premier appel affecte le résultat du second appel.

def make_withdraw(balance):
  def withdraw(amount):
    nonlocal balance
    if amount > balance:
      return 'Insufficient funds'
    balance = balance - amount
    return balance
  return withdraw
    
wd = make_withdraw(20)
wd(5)
wd(3)

Le deuxième appel à withdraw crée un deuxième cadre local, comme d'habitude. Toutefois, les deux cadres withdraw ont le même parent. Autrement dit, ils étendent l'environnement de make_withdraw, qui contient la liaison de balance. Par conséquent, ils partagent cette liaison de nom particulière. L'appel de withdraw a pour effet secondaire de modifier l'environnement qui sera prolongé par les appels futurs à withdraw. La déclaration nonlocal permet à withdraw de modifier une liaison de nom dans le cadre de make_withdraw.

Depuis que nous avons commencé à rencontrer des instructions def imbriquées, nous avons observé qu'une fonction définie localement peut rechercher des noms en dehors de ses cadres locaux. Une déclaration nonlocal n'est pas nécessaire pour accéder à un nom non local. En revanche, c'est seulement après une déclaration nonlocal qu’une fonction peut modifier la liaison des noms dans ces cadres.

Guide pratique. En introduisant des déclarations nonlocal, nous avons créé deux rôles différents pour les déclarations d'affectation. Soit elles modifient des liaisons locales, soit elles modifient les liaisons non locales. En fait, les déclarations d'affectation avaient déjà un double rôle : elles pouvaient créer de nouvelles liaisons ou re-lier des noms existants. Une affectation peut aussi modifier le contenu de listes et de dictionnaires. Les nombreux rôles de l'affectation en Python peuvent obscurcir les effets de l'exécution d'une instruction d'affectation. C'est à vous, en tant que programmeur, de documenter votre code de manière claire pour que les effets d'une affectation soient bien compris par d'autres.

Particularités Python. Ce modèle d'affectation non locale est une caractéristique générale des langages de programmation ayant des fonctions d'ordre supérieur et une portée lexicale. La plupart de ces autres langues ne requièrent aucune déclaration nonlocal. Pour eux, l'affectation non locale est souvent le comportement par défaut des instructions d'affectation.

Python a également une restriction inhabituelle concernant la recherche de noms : dans le corps d'une fonction, toutes les instances d'un nom doivent se référer au même cadre. Par conséquent, Python ne peut pas rechercher la valeur d'un nom dans un cadre non local, puis lier ce même nom dans le cadre local, car le même nom serait accessible dans deux cadres différents dans la même fonction. Cette restriction permet à Python de précalculer quel cadre contient quel nom avant même d'exécuter le corps d'une fonction. Toute violation de cette restriction entraîne l'émission d'un message d'erreur pas très clair. Pour le montrer, reprenons l'exemple make_withdraw avec l'instruction nonlocal supprimée.

def make_withdraw(balance):
  def withdraw(amount):
    if amount > balance:
      return 'Insufficient funds'
    balance = balance - amount
    return balance
  return withdraw

wd = make_withdraw(20)
wd(5)

Cela affiche l'erreur suivante :

UnboundLocalError: local variable 'balance' referenced before assignment

Cette erreur UnboundLocalError apparaît parce que balance est affecté localement à la ligne 5, et Python suppose donc que toutes les références à balance doivent également apparaître dans le cadre local. Cette erreur se produit avant même que la ligne 5 ne soit exécutée, ce qui implique que Python a examiné la ligne 5 d'une certaine manière avant d'exécuter la ligne 3. Lorsque nous étudierons la conception de l'interpréteur, nous verrons qu'il est assez courant de précalculer des informations sur le corps d'une fonction avant de l'exécuter. Dans ce cas, le prétraitement de Python a restreint le cadre dans lequel balance pourrait apparaître, empêchant ainsi que ce nom puisse être trouvé. L'ajout d'une déclaration nonlocal corrige cette erreur. La déclaration nonlocal n'existait pas en Python 2.

L'affectation non locale est une étape importante sur notre chemin vers la conception d'un programme comme une collection d'objets indépendants et autonomes, qui interagissent les uns avec les autres, mais dans lequel chacun gère son propre état interne.

En particulier, l'affectation non locale nous a permis de maintenir un état local à une fonction, mais qui évolue au fur et à mesure des appels successifs à cette fonction. Le solde balance associé à une fonction de retrait particulière est partagé entre tous les appels à cette fonction. Cependant, la liaison de ce solde associée à une instance de retrait est inaccessible au reste du programme. Seul wd est associé au cadre de make_withdraw dans lequel il a été défini. Si la fonction make_withdraw est appelée à nouveau, elle créera un cadre séparé avec une liaison distincte pour balance.

Nous pouvons étendre notre exemple pour illustrer ce point. Un deuxième appel à make_withdraw renvoie une deuxième fonction de retrait withdraw qui a un parent différent. Nous lions cette deuxième fonction au nom wd2 dans le cadre global.

def make_withdraw(balance):
    def withdraw(amount):
        nonlocal balance
        if amount > balance:
            return 'Insufficient funds'
        balance = balance - amount
        return balance
    return withdraw

wd = make_withdraw(20)
wd2 = make_withdraw(7)
wd2(6)
wd(8)

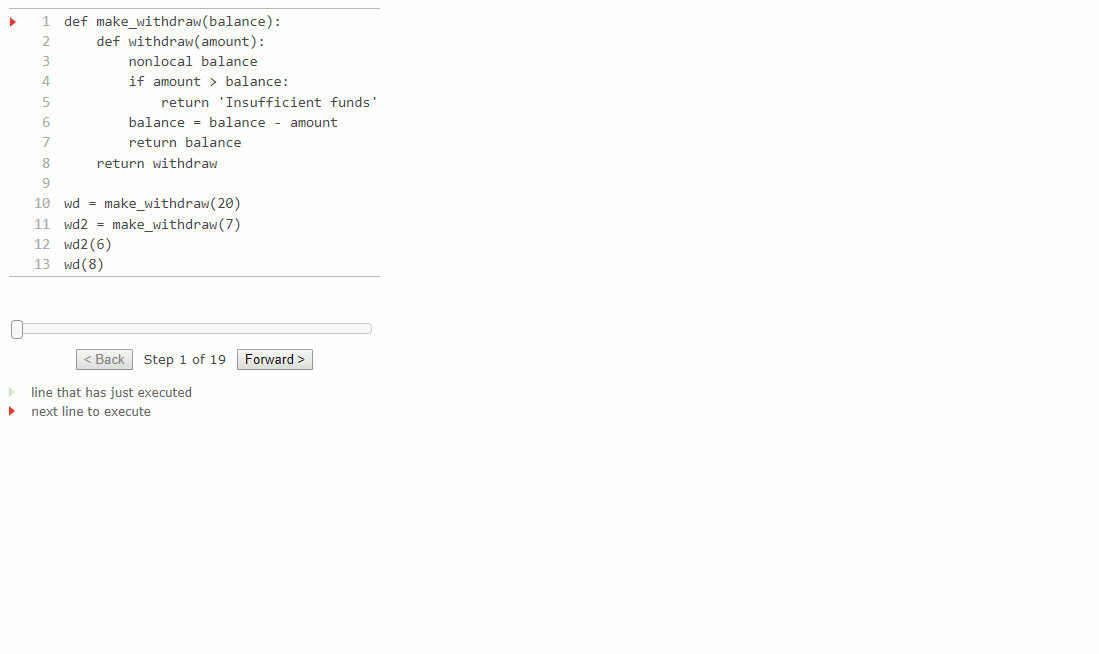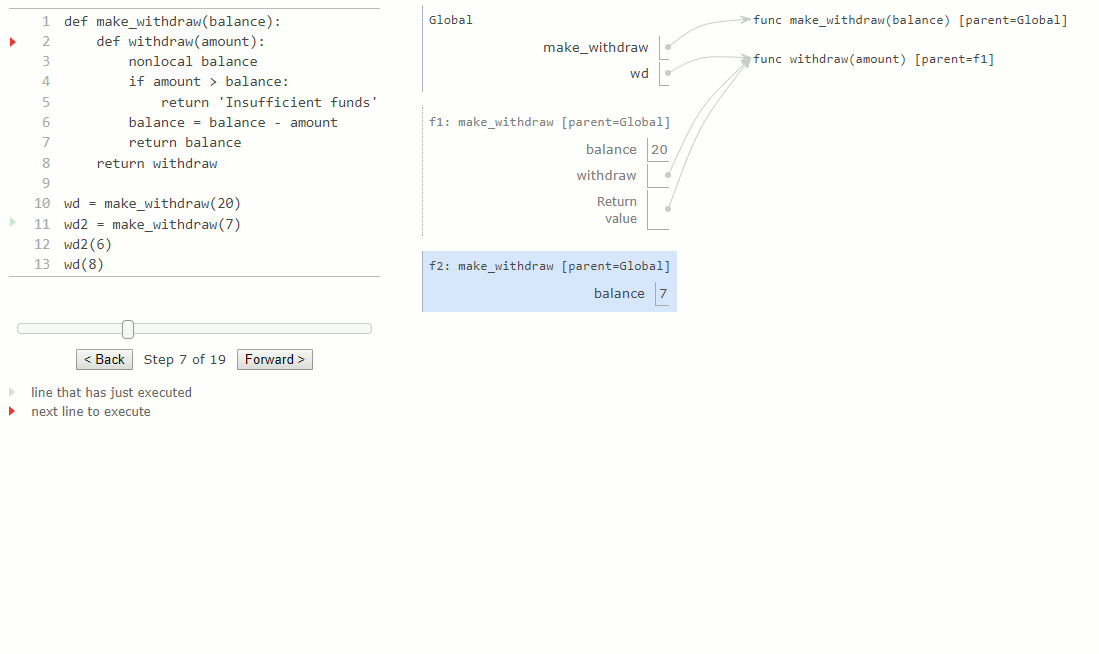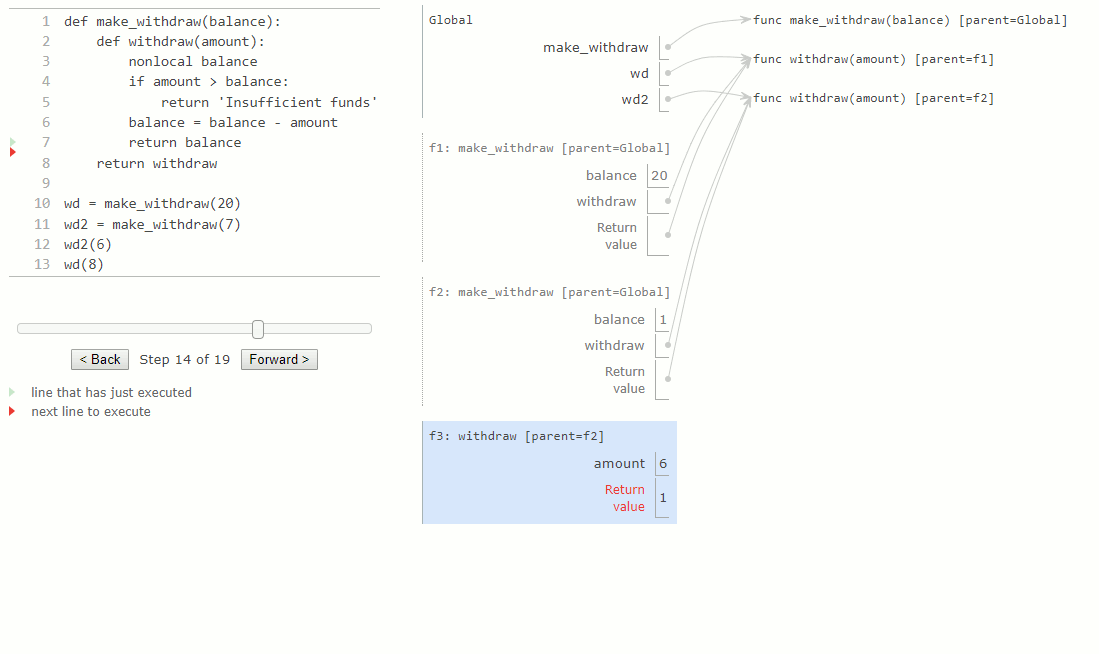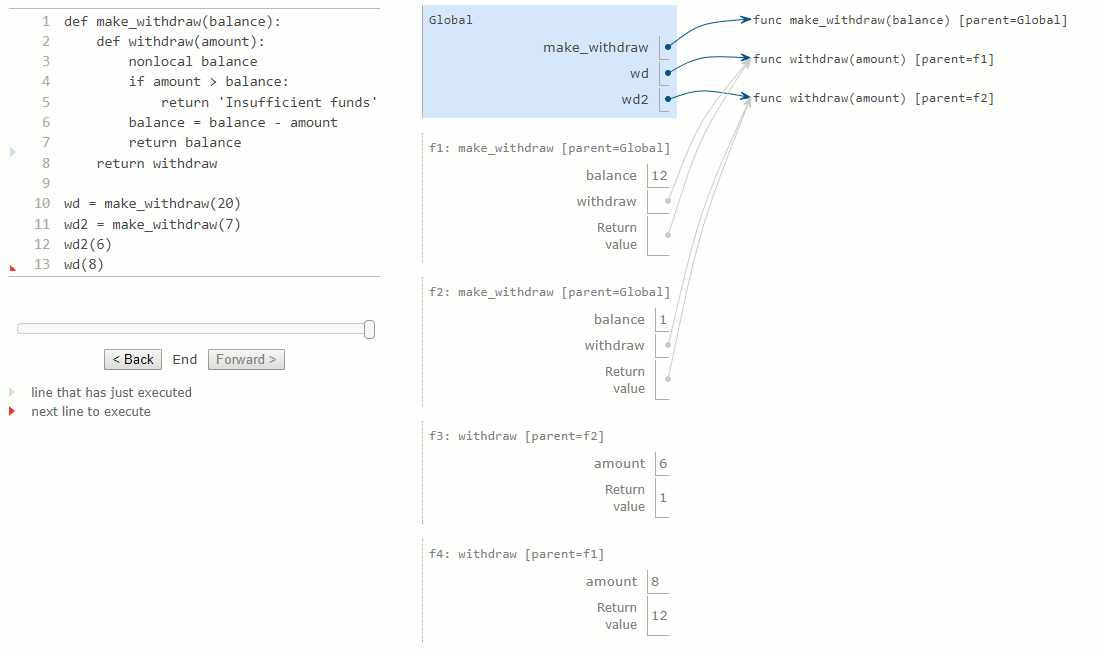
Maintenant, nous voyons qu'il existe en fait deux liaisons pour le nom balance, dans deux cadres différents, et chaque fonction de withdraw a un parent différent. Le nom wd est lié à une fonction avec un solde de 20, tandis que wd2 est lié à une fonction différente avec un solde de 7.

L'appel wd2 modifie la liaison de son nom withdraw non local, mais n'affecte pas la fonction liée au nom withdraw. Un futur appel à wd n'est pas affecté par la modification du solde de wd2 ; son solde est encore de 20.

def make_withdraw(balance):
    def withdraw(amount):
        nonlocal balance
        if amount > balance:
            return 'Insufficient funds'
        balance = balance - amount
        return balance
    return withdraw

wd = make_withdraw(20)
wd2 = make_withdraw(7)
wd2(6)
wd(8)

De cette façon, chaque instance de withdraw maintient son propre solde, mais cet état est inaccessible à toute autre fonction du programme. En regardant cette situation à un niveau supérieur, nous avons créé une abstraction d'un compte bancaire qui gère ses propres données internes, mais se comporte de manière à modéliser les comptes dans le monde : il évolue avec le temps en fonction de son historique des demandes de retrait.

Notre modèle de calcul environnemental s'étend proprement pour expliquer les effets de l'affectation non locale. Toutefois, l'affectation non locale présente quelques nuances importantes dans la façon dont nous pensons aux noms et aux valeurs.

Auparavant, nos valeurs ne changeaient pas ; seuls nos noms et liens changeaient. Lorsque deux noms a et b étaient tous deux liés à la valeur 4, il n'importait pas qu'ils soient liés aux mêmes 4 ou à des 4 différents. Pour autant que l'on pût dire, il n'y avait qu'un seul objet 4 qui ne changeait jamais.

Cependant, les fonctions avec état ne se comportent pas de cette façon. Lorsque deux noms wd et wd2 sont liés à une fonction withdraw, il importe qu'ils soient liés à la même fonction ou à différentes instances de cette fonction. Considérons l'exemple suivant, qui s'oppose celui que nous venons d'analyser. Dans ce cas, appeler la fonction nommée par wd2 a changé la valeur de la fonction nommée par wd, car les deux noms se réfèrent à la même fonction.

def make_withdraw(balance):
    def withdraw(amount):
        nonlocal balance
        if amount > balance:
            return 'Insufficient funds'
        balance = balance - amount
        return balance
    return withdraw

wd = make_withdraw(12)
wd2 = wd
wd2(1)
wd(1)

Il n'est pas rare que deux noms se réfèrent à la même valeur dans le monde, et c'est également le cas dans nos programmes. Mais, quand les valeurs changent avec le temps, nous devons faire chercher très soigneusement à comprendre l'effet d'une modification sur d'autres noms qui pourraient se référer à ces valeurs.

La clef pour analyser correctement du code ayant une affectation non locale consiste à se rappeler que seuls les appels de fonctions peuvent introduire de nouveaux cadres. Les instructions d'affectation changent toujours les liens dans des cadres existants. Dans notre cas, à moins que make_withdraw ne soit appelé deux fois, il ne peut y avoir qu'une seule liaison pour le nom balance.

Identité et changement. Ces subtilités surviennent parce que, en introduisant des fonctions non-pures qui modifient l'environnement non local, nous avons changé la nature des expressions. Une expression qui ne contient que des appels de fonctions pures est dite référentiellement transparente : sa valeur ne change pas si nous substituons l'une de ses sous-expressions à la valeur de cette sous-expression.

Les opérations de re-liaison violent les conditions de transparence référentielle parce qu'elles font plus que renvoyer une valeur : elles modifient l'environnement. Lorsque nous introduisons une re-liaison quelconque, nous rencontrons un problème épistémologique épineux : que veut dire que deux valeurs sont les mêmes ? Dans notre modèle d'environnement de calcul, deux fonctions définies séparément ne sont pas les mêmes, car des modifications apportées à l'une peuvent ne pas affecter l'autre.

En général, tant que nous ne modifions jamais les objets de données, nous pouvons considérer un objet de données composé comme étant précisément la totalité de ses composants. Par exemple, un nombre rationnel est déterminé en donnant son numérateur et son dénominateur. Mais cette vue n'est plus valide en présence d'un changement, dans lequel un objet de données composé possède une « identité » différente des composants dont il est formé. Un compte bancaire est toujours « le même » compte bancaire même si nous changeons le solde en effectuant un retrait. À l'inverse, nous pourrions avoir deux comptes bancaires qui ont le même solde, mais sont des objets différents.

Malgré les complications qu'elle introduit, l'affectation non locale est un outil puissant pour créer des programmes modulaires. Les différentes parties d'un programme, qui correspondent à différents cadres d'environnement, peuvent évoluer séparément tout au long de l'exécution du programme. En outre, en utilisant des fonctions avec l'état local, nous sommes en mesure de mettre en œuvre des types de données mutables. En fait, nous pouvons mettre en place des types de données abstraits qui sont équivalents aux types internes list et dict introduits précédemment.

Le langage Python ne nous donne pas accès à la mise en œuvre des listes, mais seulement à l'abstraction et aux méthodes de mutation de séquences intégrées dans le langage. Pour comprendre comment une liste mutable pourrait être représentée à l'aide de fonctions avec l'état local, nous allons maintenant développer une implémentation d'une liste chaînée mutable.

Nous représenterons une liste chaînée mutable par une fonction qui a une liste chaînée dans son état local. Les listes doivent avoir une identité, comme toute valeur mutable. En particulier, nous ne pouvons pas utiliser None pour représenter une liste mutable vide, car deux listes vides ne sont pas des valeurs identiques (par exemple, ajouter un élément à l'une d'elles n'affecte pas à l'autre), mais None est None. D'un autre côté, deux fonctions différentes ayant toutes deux un état local empty permettront de distinguer deux listes vides.

Si une liste chaînée mutable est une fonction, quels arguments prend-elle ? La réponse illustre un modèle général de programmation : la fonction est une fonction de distribution (dispatch function) et ses arguments sont un message suivi des arguments supplémentaires pour paramétrer cette méthode. Ce message est une chaîne de caractères indiquant ce que la fonction doit faire. Les fonctions de distribution sont en réalité de nombreuses fonctions en une seule : le message détermine le comportement de la fonction, et les arguments supplémentaires sont utilisés dans ce comportement.

Notre liste mutable répondra à cinq messages différents : len, getitem, push_first, pop_first et str. Les deux premiers mettent en œuvre les comportements de l'abstraction de la séquence. Les deux suivants permettent d'ajouter ou de supprimer le premier élément de la liste. Le dernier message renvoie une représentation sous la forme de chaîne de caractères de l'ensemble de la liste chaînée.

>>> def mutable_link():
        """Return a functional implementation of a mutable linked list."""
        contents = empty
        def dispatch(message, value=None):
            nonlocal contents
            if message == 'len':
                return len_link(contents)
            elif message == 'getitem':
                return getitem_link(contents, value)
            elif message == 'push_first':
                contents = link(value, contents)
            elif message == 'pop_first':
                f = first(contents)
                contents = rest(contents)
                return f
            elif message == 'str':
                return join_link(contents, ", ")
        return dispatch

Nous pouvons aussi ajouter une fonction pratique pour construire fonctionnellement une liste chaînée à partir de toute séquence du langage, en ajoutant simplement chaque élément dans l'ordre inverse.

>>> def to_mutable_link(source):
        """Return a functional list with the same contents as source."""
        s = mutable_link()
        for element in reversed(source):
            s('push_first', element)
        return s

Dans la définition ci-dessus, la fonction reversed prend et retourne une valeur itérable ; c'est un autre exemple d'une fonction qui traite les séquences.

Nous pouvons maintenant construire des listes chaînées mutables mises en œuvre fonctionnellement. Notez que la liste chaînée elle-même est une fonction.

>>> s = to_mutable_link(suits)
>>> type(s)
<class 'function'>
>>> print(s('str'))
heart, diamond, spade, club

En outre, nous pouvons transmettre à la liste s des messages qui changent son contenu, par exemple enlever le premier élément.

>>> s('pop_first')
'heart'
>>> print(s('str'))
diamond, spade, club

En principe, les opérations push_first et pop_first suffisent à apporter des modifications arbitraires à une liste. Nous pouvons toujours vider la liste entièrement et remplacer son ancien contenu par le résultat souhaité.

Le passage de messages. En y consacrant les efforts nécessaires, nous pourrions mettre en place les nombreuses opérations de mutation utiles de listes Python, comme extend et insert. Nous devrions faire un choix : nous pourrions les mettre en œuvre sous la forme de fonctions qui utilisent les messages existants pop_first et push_first pour faire tous ces changements. L'autre solution serait d'ajouter au corps de la fonction dispatch d' autres clauses elif qui s'appliqueraient chacune à un message donné (par exemple, extend) et effectueraient directement les changements voulus à contents.

Cette deuxième approche, qui encapsule la logique de toutes les opérations sur une donnée dans une fonction qui répond aux différents messages, est une discipline appelée passage de messages. Un programme qui utilise le passage de messages définit des fonctions de distribution, qui peuvent chacune avoir un état local, et organise le calcul en passant des « messages » comme premier argument à ces fonctions. Les messages sont des chaînes de caractères qui correspondent à des comportements particuliers.

Mise en œuvre de dictionnaires. Nous pouvons également mettre en œuvre une valeur avec un comportement similaire à un dictionnaire. Dans ce cas, nous utilisons une liste de paires clé-valeur pour stocker le contenu du dictionnaire. Chaque paire est une liste à deux éléments.

>>> def dictionary():
        """Return a functional implementation of a dictionary."""
        records = []
        def getitem(key):
            matches = [r for r in records if r[0] == key]
            if len(matches) == 1:
                key, value = matches[0]
                return value
        def setitem(key, value):
            nonlocal records
            non_matches = [r for r in records if r[0] != key]
            records = non_matches + [[key, value]]
        def dispatch(message, key=None, value=None):
            if message == 'getitem':
                return getitem(key)
            elif message == 'setitem':
                setitem(key, value)
        return dispatch

Une nouvelle fois, nous utilisons la méthode de passage de messages pour organiser notre mise en œuvre. Nous mettons en place deux messages : getitem et setitem. Pour insérer une valeur pour une clef, nous filtrons tous les enregistrements existants avec la clef donnée, puis ajoutons l'enregistrement désiré. De cette façon, nous sommes assurés que chaque clef n'apparaît qu'une seule fois. Pour rechercher une valeur correspondant à une clef, nous filtrons l'enregistrement qui correspond à la clef donnée. Nous pouvons maintenant utiliser notre application pour stocker et récupérer des valeurs.

>>> d = dictionary()
>>> d('setitem', 3, 9)
>>> d('setitem', 4, 16)
>>> d('getitem', 3)
9
>>> d('getitem', 4)
16

Cette mise en œuvre d'un dictionnaire n'est pas optimisée pour la recherche rapide d'enregistrement, parce que chaque appel doit filtrer tous les enregistrements. Le type dictionnaire intégré dans Python est beaucoup plus efficace. La façon dont ce type est mis en œuvre en Python dépasse le cadre de ce texte.

La fonction dispatch est une méthode générale de mise en œuvre d'une interface de passage de message pour les données abstraites. Pour mettre en œuvre l'envoi de messages, nous avons jusqu'ici utilisé des instructions conditionnelles pour comparer la chaîne de message à un ensemble fixe de messages connus.

Le type de données dictionnaire fournit une méthode générale pour rechercher une valeur correspondant à une clef. Au lieu d'utiliser des conditions de type if ... elif ... pour déterminer une action à effectuer, nous pouvons utiliser des dictionnaires avec des chaînes de caractères comme clefs.

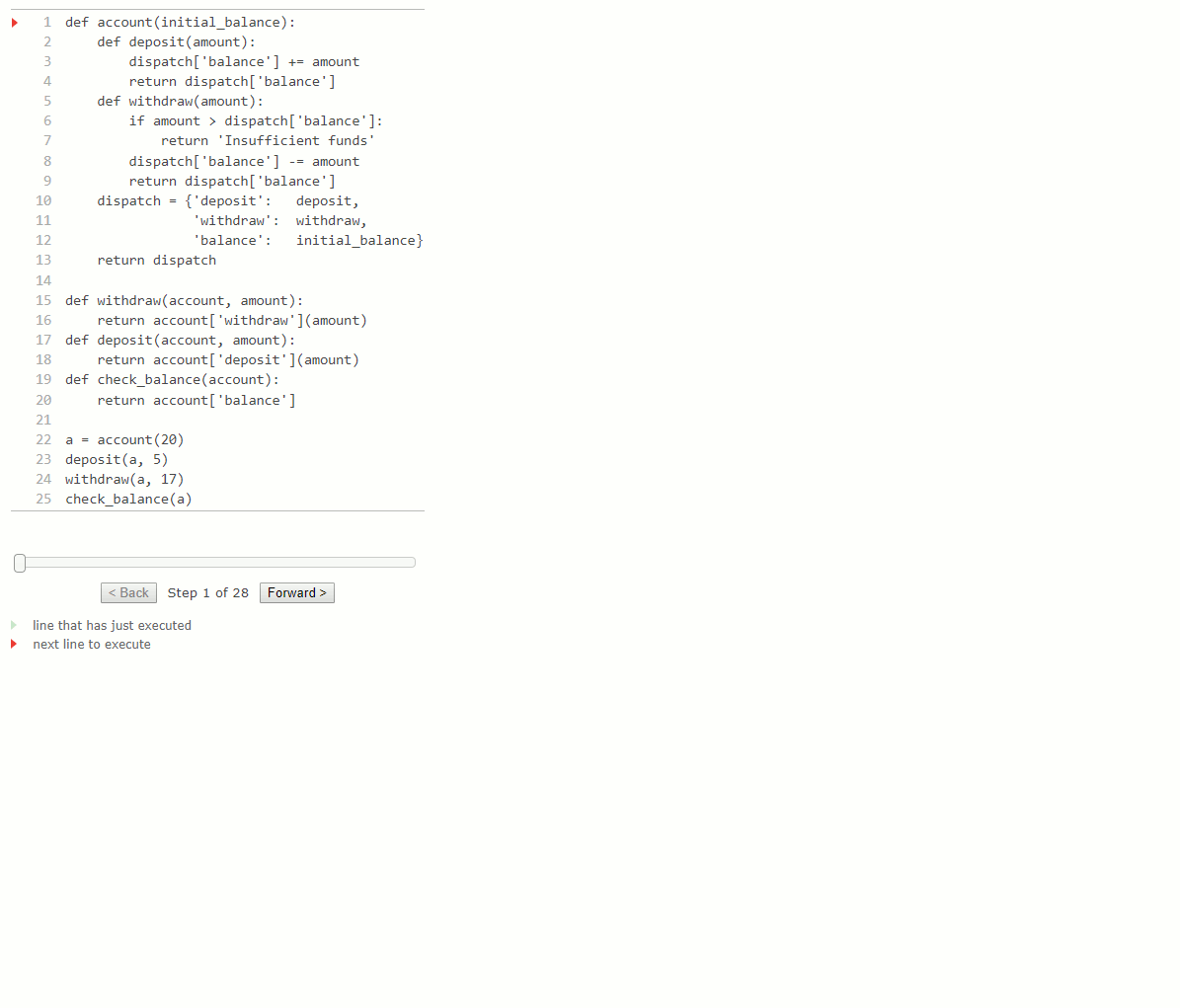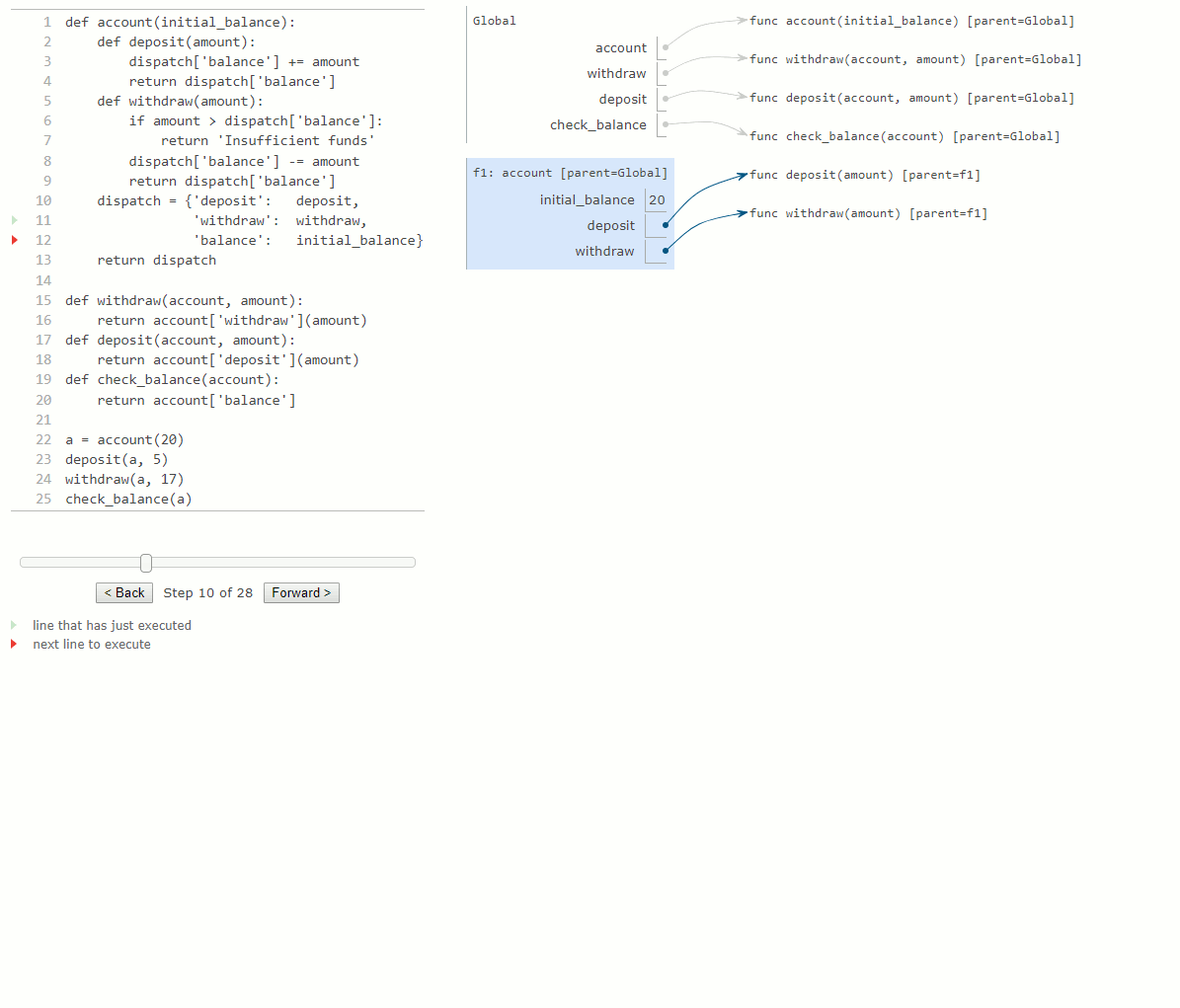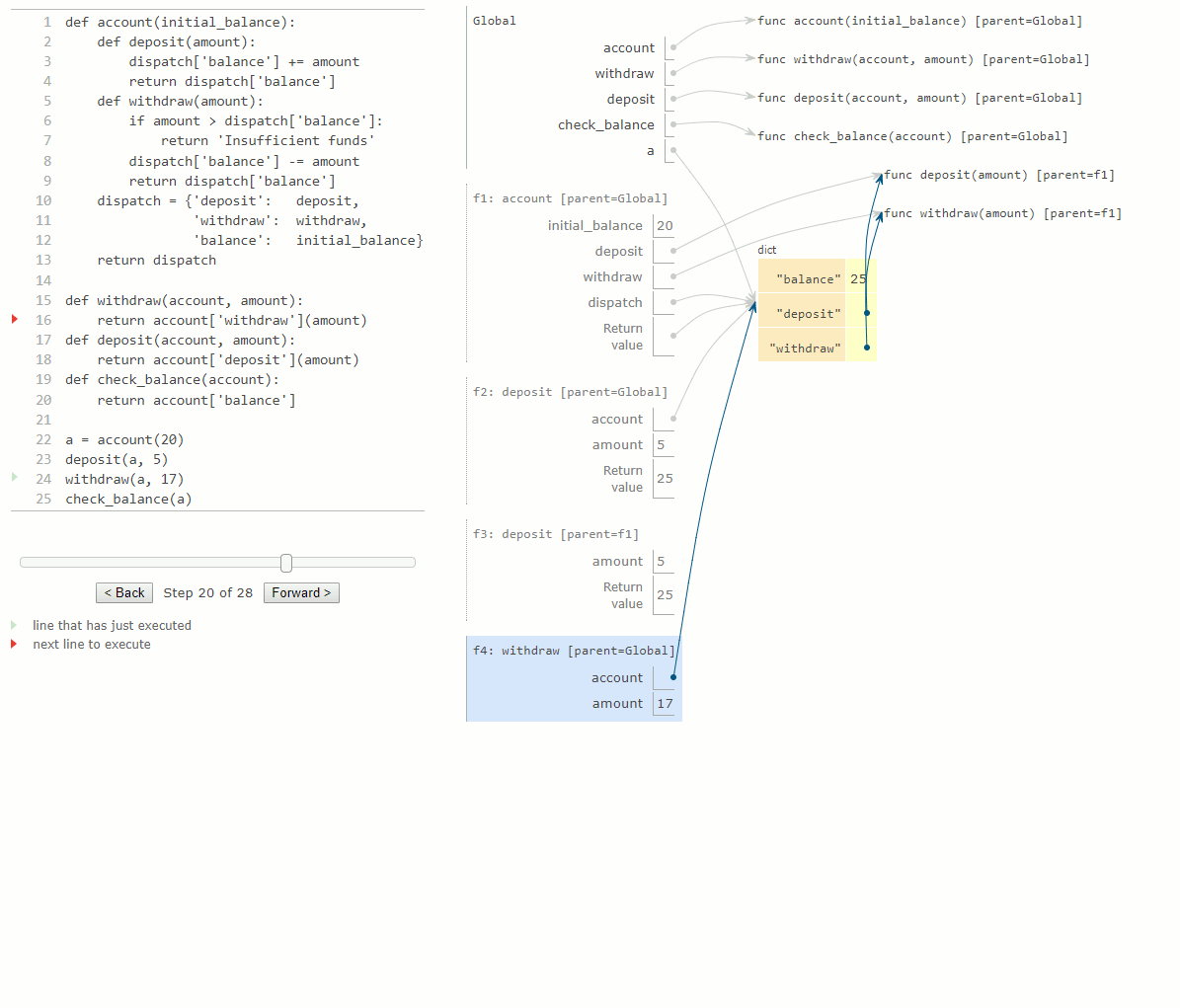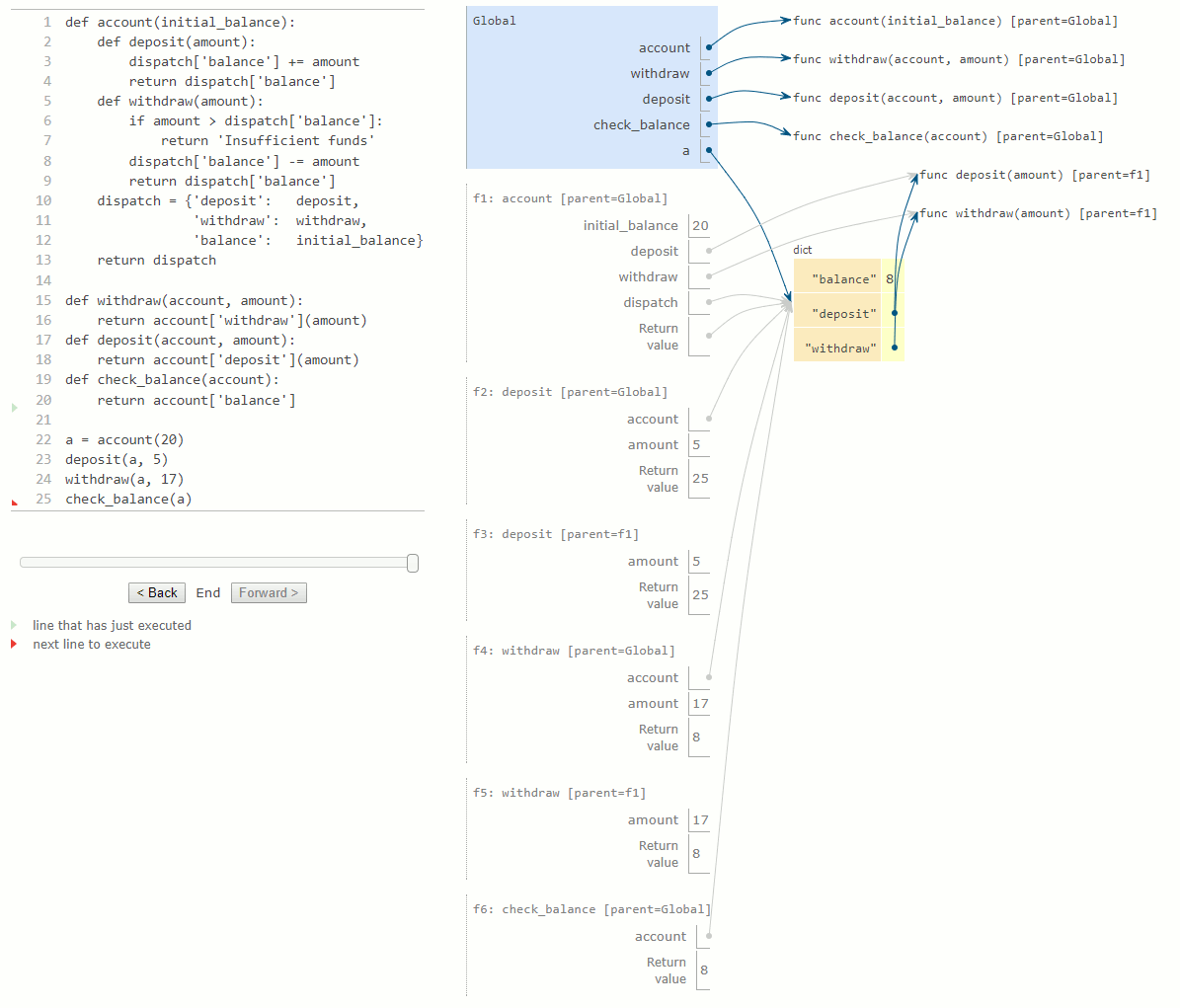
Le type de données mutable account ci-dessous utilise un dictionnaire. Il a un constructeur account et un sélecteur check_balance, ainsi que des fonctions de deposit ou withdraw pour déposer ou retirer des fonds. De plus, l'état local du compte est stocké dans le dictionnaire, de même que les fonctions qui mettent en œuvre son comportement.

def account(initial_balance):
    def deposit(amount):
        dispatch['balance'] += amount
        return dispatch['balance']
    def withdraw(amount):
        if amount > dispatch['balance']:
            return 'Insufficient funds'
        dispatch['balance'] -= amount
        return dispatch['balance']
    dispatch = {'deposit':   deposit,
                'withdraw':  withdraw,
                'balance':   initial_balance}
    return dispatch

def withdraw(account, amount):
    return account['withdraw'](amount)
def deposit(account, amount):
    return account['deposit'](amount)
def check_balance(account):
    return account['balance']

a = account(20)
deposit(a, 5)
withdraw(a, 17)
check_balance(a)

Le nom dispatch dans le corps du constructeur account est lié à un dictionnaire contenant les messages acceptés comme clefs par un compte. Le solde (balance) est un nombre, tandis que les messages de dépôt et de retrait sont liés à des fonctions. Ces fonctions ont accès au dictionnaire dispatch, et elles peuvent lire et modifier le solde. En stockant le solde dans le dictionnaire dispatch plutôt que dans le cadre account directement, nous évitons la nécessité de déclarations de type nonlocal dans deposit et withdraw.

Les opérateurs += et -= sont un raccourci en Python (et beaucoup d'autres langages de programmation) pour la lecture d'une valeur et la réaffectation. Les deux dernières lignes ci- dessous sont équivalentes.

>>> a = 2
>>> a = a + 1
>>> a += 1

Les données mutables nous permettent non seulement de simuler des systèmes subissant des changements, mais aussi de construire de nouveaux types d'abstractions. Dans cet exemple étendu, nous combinons des affectations de type nonlocal, des listes et des dictionnaires pour construire un système basé sur des contraintes qui prend en charge des calculs dans plusieurs directions. Exprimer des programmes sous la forme de contraintes est une forme de programmation déclarative, dans laquelle un programmeur déclare la structure d'un problème à résoudre, mais fait abstraction des détails de la façon dont est calculée la solution au problème.

Les programmes informatiques sont traditionnellement organisés comme des calculs unidirectionnels, qui effectuent des opérations sur des arguments préspécifiés pour produire des résultats souhaités. D'un autre côté, nous voulons souvent modéliser des systèmes en termes de relations entre des quantités. Par exemple, nous avons considéré précédemment la loi des gaz parfaits, qui relie la pression (p), le volume (v), la quantité (n) et la température (t) d'un gaz idéal grâce à la constante de Boltzmann (k) :

p * v = n * k * t

Une telle équation n'est pas unidirectionnelle. Si nous avons quatre de ces valeurs, nous pouvons utiliser cette équation pour calculer la cinquième. Pourtant, la traduction de l'équation dans un langage informatique traditionnel nous forcerait à choisir l'une des quantités à calculer en termes de quatre autres. Ainsi, une fonction de calcul de la pression ne peut pas être utilisée pour calculer la température, même si les calculs des deux quantités proviennent de la même équation.

Dans cette section, nous esquissons la conception d'un modèle général des relations linéaires. Nous définissons les contraintes primitives qui s'appliquent à des quantités, par exemple une contrainte adder (a, b, c) qui applique la relation mathématique a + b = c .

Nous définissons aussi un moyen de combiner des contraintes primitives pour exprimer des relations plus complexes. De cette façon, notre programme ressemble à un langage de programmation. Nous combinons des contraintes en construisant un réseau dans lequel les contraintes sont reliées entre elles par des connecteurs. Un connecteur est un objet qui « contient » une valeur et peut participer à une ou plusieurs contraintes.

Par exemple, nous savons que la relation entre les températures mesurées en degrés Fahrenheit et Celsius est :

9 * c = 5 * (f – 32)

Cette équation est une contrainte complexe entre c et f. Une telle contrainte peut être considérée comme un réseau constitué de contraintes primitives de types additionneur, multiplicateur et constante.

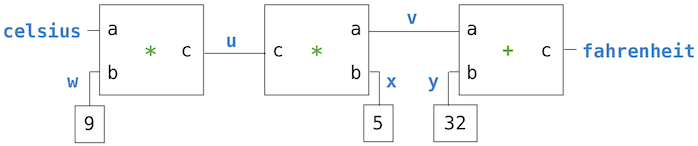
Dans cette figure, on voit sur la gauche une boîte multiplicateur avec trois bornes, étiquetée a, b et c. Celles-ci relient le multiplicateur au reste du réseau de la façon suivante : la borne a est reliée au connecteur celsius, qui contiendra la température en degrés Celsius. La borne b est reliée au connecteur w, qui est lui-même relié à une boîte constante, dont la valeur est 9. La borne c, que la boîte multiplicateur contraint à être le produit d' a et b, est reliée à la borne c d'un autre multiplicateur, dans lequel b est relié à une constante 5 et a relié à l'un des termes d'une contrainte de type additionneur.

Le calcul par un tel réseau se déroule comme suit : lorsqu'un connecteur reçoit une valeur (de la part de l'utilisateur ou par une boîte de contrainte auquel il est relié), il réveille toutes les contraintes auxquelles il est associé (à l' exception de la contrainte qui vient de le réveiller) pour les informer qu'il a une valeur. Chaque boîte de contrainte réveillée sonde alors ses connecteurs pour voir s'il y a suffisamment d'informations pour déterminer une valeur pour un connecteur. Si c'est le cas, la boîte attribue une valeur à ce connecteur, qui réveille alors à son tour toutes les contraintes qui lui sont associées, et ainsi de suite. Par exemple, dans la conversion entre degrés Celsius et Fahrenheit, w, x et y sont alimentées dès le départ par les boîtes constantes à 9, 5, et 32, respectivement. Les connecteurs réveillent les multiplicateurs et l'additionneur, qui déterminent qu'il n'y a pas suffisamment d'informations pour continuer. Si l'utilisateur (ou une autre partie du réseau) attribue une valeur (disons 25) au connecteur celsius, le multiplicateur de gauche est réveillé, et u sera positionné à 25 * 9 = 225. Puis u réveille le second multiplicateur, qui affecte 225/5 = 45 à v, et v réveille l'additionneur, qui fixe le connecteur fahrenheit à 77.

Utilisation du système de contrainte. Pour utiliser le système de contrainte afin d'effectuer le calcul de la température décrit ci-dessus, nous créons d'abord deux connecteurs, nommés celsius et fahrenheit, en appelant le constructeur connector.

>>> celsius = connector('Celsius')
>>> fahrenheit = connector('Fahrenheit')

Ensuite, nous relions ces connecteurs à un réseau qui reflète la figure ci-dessus. La fonction converter assemble les différents connecteurs et les contraintes du réseau.

>>> def converter(c, f):
        """Connect c to f with constraints to convert from Celsius to Fahrenheit."""
        u, v, w, x, y = [connector() for _ in range(5)]
        multiplier(c, w, u)
        multiplier(v, x, u)
        adder(v, y, f)
        constant(w, 9)
        constant(x, 5)
        constant(y, 32)

>>> converter(celsius, fahrenheit)

Nous allons utiliser un système de transmission de messages pour coordonner les contraintes et les connecteurs. Les contraintes sont des dictionnaires qui ne détiennent pas eux-mêmes d'états locaux. Leurs réponses aux messages sont des fonctions non-pures qui changent les connecteurs qu'ils contraignent.

Les connecteurs sont des dictionnaires qui possèdent une valeur courante et répondent aux messages qui manipulent cette valeur. Les contraintes ne changeront pas la valeur des connecteurs directement, mais le feront en envoyant des messages, de sorte que le connecteur peut informer les autres contraintes en réaction au changement. De cette façon, un connecteur représente un nombre, mais encapsule aussi le comportement du connecteur.

Un message que nous pouvons envoyer à un connecteur est une définition de sa valeur. Ici, nous (le 'user') définissons la valeur de celsius à 25.

>>> celsius['set_val']('user', 25)
Celsius = 25
Fahrenheit = 77.0

Non seulement la valeur de celsius passe à 25, mais sa valeur se propage à travers le réseau, et la valeur de fahrenheit est également modifiée. Ces changements sont affichés parce que nous avons appelé ces deux connecteurs lorsque nous les construisons.

Maintenant, nous pouvons essayer d'affecter à fahrenheit une nouvelle valeur, disons 212.

>>> fahrenheit['set_val']('user', 212)
Contradiction detected: 77.0 vs 212

Le connecteur se plaint qu'il a détecté une contradiction : sa valeur est 77,0, et quelqu'un essaie de le mettre à 212. Si nous voulons vraiment réutiliser le réseau avec de nouvelles valeurs, nous pouvons dire à celsius d'oublier son ancienne valeur :

>>> celsius['forget']('user')
Celsius is forgotten
Fahrenheit is forgotten

Le connecteur celsius s'aperçoit que l'utilisateur user, qui avait donné une valeur à l'origine, supprimait maintenant cette valeur ; celsius accepte donc de perdre sa valeur, et il informe le reste du réseau de ce changement. Cette information se propage finalement à Fahrenheit, qui constate maintenant qu'il n'a aucune raison de continuer à croire que sa propre valeur est 77. Par conséquent, il abandonne également sa valeur.

Maintenant que fahrenheit n'a plus de valeur, nous sommes libres de la fixer à 212 :

>>> fahrenheit['set_val']('user', 212)
Fahrenheit = 212
Celsius = 100.0

Cette nouvelle valeur se propage à travers le réseau et force celsius à prendre une valeur de 100. Nous avons utilisé le même réseau pour calculer celsius à partir de fahrenheit et pour calculer fahrenheit à partir de celsius. Cette non-directionnalité du calcul est la principale caractéristique des systèmes à base de contraintes.

La mise en œuvre du système de contraintes. Comme nous l'avons vu, les connecteurs sont des dictionnaires qui associent les noms des messages à des fonctions et les valeurs de données. Nous allons mettre en place des connecteurs qui répondent aux messages suivants :

• connector['set_val'](source, value) indique que la source demande au connecteur de positionner sa valeur courante à value.
• connector['has_val']() indique si le connecteur a déjà une valeur.
• connector['val'] renvoie la valeur actuelle du connecteur.
• connector['forget'](source) indique au connecteur que la source lui demande d'oublier sa valeur.
• connector['connect'](source) demande au connecteur de participer à une nouvelle contrainte, la source.

Les contraintes sont aussi des dictionnaires, qui reçoivent des informations des connecteurs au moyen de deux messages :

• constraint['new_val']() indique qu'un connecteur relié à la contrainte a une nouvelle valeur.
• constraint['forget']() indique qu'un connecteur relié à la contrainte a oublié sa valeur.

Lorsque les contraintes reçoivent ces messages, elles les propagent de manière appropriée à d'autres connecteurs.

La fonction adder construit sur trois connecteurs une contrainte d'addition selon laquelle la somme des deux premiers doit être égale au troisième : a + b = c. Pour permettre la propagation de contrainte multidirectionnelle, l'addition doit également préciser qu'il retranche a de c pour obtenir b et soustrait également b de c pour obtenir a.

>>> from operator import add, sub
>>> def adder(a, b, c):
        """The constraint that a + b = c."""
        return make_ternary_constraint(a, b, c, add, sub, sub)

Nous voudrions mettre en œuvre une contrainte ternaire générique qui utilise les trois connecteurs et trois fonctions de adder pour créer une contrainte qui accepte les messages new_val et forget. Les réponses aux messages sont des fonctions locales qui sont placées dans un dictionnaire appelé contrainte.

>>> def make_ternary_constraint(a, b, c, ab, ca, cb):
        """The constraint that ab(a,b)=c and ca(c,a)=b and cb(c,b) = a."""
        def new_value():
            av, bv, cv = [connector['has_val']() for connector in (a, b, c)]
            if av and bv:
                c['set_val'](constraint, ab(a['val'], b['val']))
            elif av and cv:
                b['set_val'](constraint, ca(c['val'], a['val']))
            elif bv and cv:
                a['set_val'](constraint, cb(c['val'], b['val']))
        def forget_value():
            for connector in (a, b, c):
                connector['forget'](constraint)
        constraint = {'new_val': new_value, 'forget': forget_value}
        for connector in (a, b, c):
            connector['connect'](constraint)
        return constraint

Le dictionnaire appelé constraint est une table de distribution, mais représente aussi l'objet contrainte lui-même. Il réagit aux deux messages que les contraintes reçoivent, mais il est également passé comme source de l'argument dans les appels à ses connecteurs.

La fonction locale new_value de la contrainte est appelée chaque fois que la contrainte est informée que l'un de ses connecteurs a une valeur. Cette fonction vérifie d'abord si a et b ont tous deux des valeurs. Si oui, il dit à c de prendre pour valeur la valeur de retour de la fonction ab, qui est add dans le cas d'un additionneur. La contrainte se passe elle-même (constraint) en tant que source de l'argument du connecteur, qui est l'objet additionneur. Si a et b n'ont pas tous les deux une valeur, la contrainte vérifie a et c, et ainsi de suite.

Si la contrainte est informée que l'un de ses connecteurs a oublié sa valeur, il demande à tous ses connecteurs d'oublier désormais leurs valeurs. (Seules les valeurs définies par cette contrainte sont effectivement perdues.)

Un multiplicateur est très similaire à un additionneur.

>>> from operator import mul, truediv
>>> def multiplier(a, b, c):
        """The constraint that a * b = c."""
        return make_ternary_constraint(a, b, c, mul, truediv, truediv)

Une constante est aussi une contrainte, mais à laquelle on n'envoie jamais de message, car elle ne contient qu'un seul connecteur dont la valeur est fixée lors de la construction.

>>> def constant(connector, value):
        """The constraint that connector = value."""
        constraint = {}
        connector['set_val'](constraint, value)
        return constraint

Ces trois contraintes sont suffisantes pour mettre en œuvre notre réseau de conversion de température.

Représentation des connecteurs. Un connecteur est représenté comme un dictionnaire qui contient une valeur, mais a également des fonctions de réponse ayant un état local. Le connecteur doit garder la trace de l'informateur (informant) qui lui a donné sa valeur actuelle, et une liste des contraintes auxquelles il participe.

Le constructeur connector a des fonctions locales pour définir et oublier les valeurs qui sont des réactions aux messages reçus des contraintes.

>>> def connector(name=None):
        """A connector between constraints."""
        informant = None
        constraints = []
        def set_value(source, value):
            nonlocal informant
            val = connector['val']
            if val is None:
                informant, connector['val'] = source, value
                if name is not None:
                    print(name, '=', value)
                inform_all_except(source, 'new_val', constraints)
            else:
                if val != value:
                    print('Contradiction detected:', val, 'vs', value)
        def forget_value(source):
            nonlocal informant
            if informant == source:
                informant, connector['val'] = None, None
                if name is not None:
                    print(name, 'is forgotten')
                inform_all_except(source, 'forget', constraints)
        connector = {'val': None,
                     'set_val': set_value,
                     'forget': forget_value,
                     'has_val': lambda: connector['val'] is not None,
                     'connect': lambda source: constraints.append(source)}
        return connector

Un connecteur est à nouveau un dictionnaire faisant office de table de distribution pour les cinq messages utilisés par les contraintes pour communiquer avec les connecteurs. Quatre réponses sont des fonctions, et la dernière est la valeur elle-même.

La fonction locale set_value est appelée quand il y a une demande d'affectation de la valeur du connecteur. Si le connecteur n'a pas de valeur, il prendra la valeur reçue et se souviendra que c'est la contrainte source informant qui lui a demandé de prendre cette valeur. Ensuite, le connecteur informera toutes les contraintes auxquelles il participe, à l'exception de celle qui lui a demandé de prendre cette valeur. On accomplit ceci en utilisant la fonction itérative suivante :

>>> def inform_all_except(source, message, constraints):
        """Inform all constraints of the message, except source."""
        for c in constraints:
            if c != source:
                c[message]()

Si l'on demande à un connecteur d'oublier sa valeur, il appelle la fonction locale forget-value, qui vérifie d'abord que la demande provient de la contrainte qui a défini sa valeur à l'origine. Si oui, le connecteur informe les contraintes auxquelles il est associé de la perte de la valeur.

La réponse au message has_val indique si le connecteur a une valeur. La réponse au message connect ajoute la contrainte source à la liste des contraintes.

Le programme de contraintes que nous avons mis en place a introduit de nombreuses idées qui apparaîtront à nouveau dans la programmation orientée objet. Les contraintes et les connecteurs sont les deux abstractions qui sont manipulées par le biais de messages. Lorsque la valeur d'un connecteur est modifiée, ce changement est effectué par un message qui non seulement modifie la valeur, mais effectue la validation (vérification de la source) et propage ses effets (informer les autres contraintes). En fait, nous allons utiliser une architecture similaire de dictionnaires avec des clés sous forme de chaîne et des valeurs fonctionnelles pour mettre en œuvre un système orienté objet plus loin dans ce tutoriel.