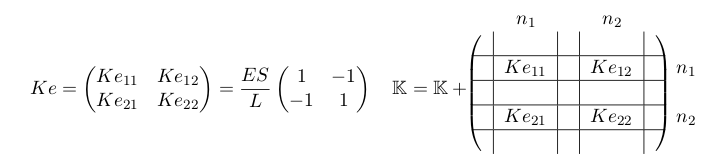I. Installation de Python▲
I-A. Généralités sur Python▲
Python est un langage open source multiplateforme. Son intérêt réside notamment dans les nombreuses bibliothèques qu'il propose. Dans le domaine du calcul scientifique, nous montrerons qu'il remplace avantageusement MATLAB.
Nous utiliserons Spyder, un éditeur de texte libre lui aussi, qui nous permettra d'avoir une interface interactive qui ne dépaysera pas les habitués de MATLAB.
Il existe bien sûr d'autres éditeurs de texte que vous pouvez utiliser si vous le préférez. Les installations proposées après installent Python, numpy et scipy. Si vous voulez utiliser un autre éditeur, assurez-vous d'avoir ces paquets installés.
I-B. Sous Linux▲
Pour les utilisateurs de Debian ou d'Ubuntu, cette ligne de commande suffit à installer. Connectez-vous en superutilisateur pour l'exécuter :
aptitude install spyderPour utilisateurs d'autres distributions Linux, se référer à votre gestionnaire de paquets qui doit proposer Spyder.
I-C. Sous Windows▲
Pour installer Spyder, Python et les bibliothèques que nous allons utiliser, le plus simple et d'installer une distribution scientifique qui comporte tout cela.
Je vous propose winPython.
Sur la page de téléchargements, choisir votre fichier d'installation en fonction de l'architecture de votre ordinateur. En général la version 64 bits convient. La procédure d'installation est classique.
II. Premiers pas sur Python, utilisation de Spyder▲
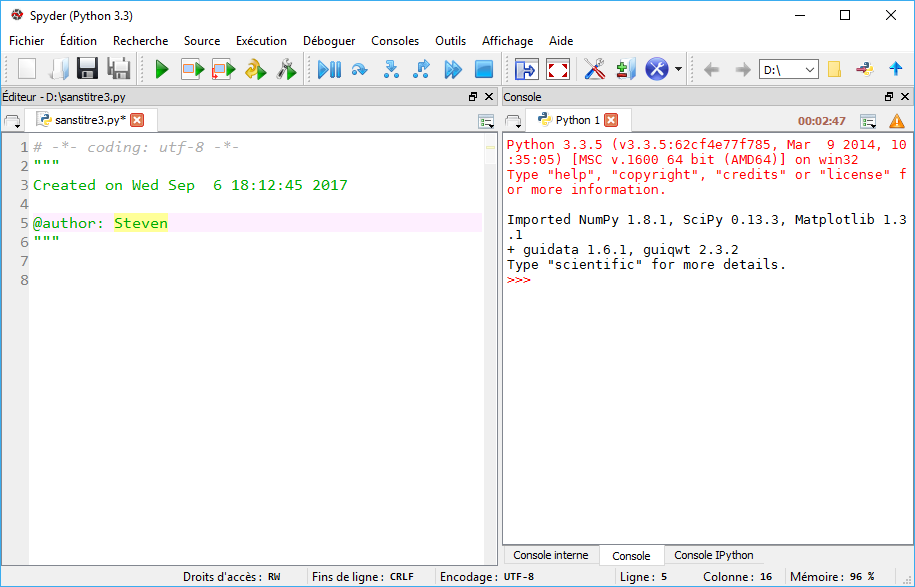
Spyder est un environnement de développement sous Python qui permet sur une même fenêtre d'éditer un fichier Python et de l'exécuter.
Deux sous-fenêtres sont donc absolument indispensables : l'éditeur et la console.
Je vous conseille de maximiser en largeur la taille de l'éditeur, car c'est cette fenêtre dans laquelle vous passerez le plus de temps, et ensuite de maximiser la taille de la console notamment en hauteur.
Les autres fenêtres ne sont pas indispensables, vous pouvez les fermer pour l'instant pour économiser de la place pour l'éditeur et la console.
L'intérêt de Spyder est d'éditer un fichier, puis en appuyant sur F5 il est exécuté dans la console. On peut alors voir le résultat de nos modifications en direct.
Créez un nouveau fichier. Enregistrez-le où vous voulez. Spyder vous a généré un code minimaliste qui ressemble à celui-ci :
2.
3.
4.
5.
6.
# -*- coding: utf-8 -*-
"""
Created on Tue Dec 24 17:07:37 2013
@author: steven
"""
La première ligne précise l'encodage. Cela permet notamment d'afficher les caractères spéciaux proprement. Dans mon cas, sous Linux c'est de l'UFT-8.
Les lignes suivantes, entourées de """ sont une description de votre code, vous pouvez renseigner le but de votre script, l'auteur, etc.
Ajoutez la ligne suivante à la fin de votre fichier :
print ("Ça marche!")Appuyez ensuite sur F5. Si une boîte de dialogue s'ouvre pour vous demander les options d'exécution, cochez « Exécuter dans l'interpréteur Python » actif puis validez.
Vous devriez voir dans la console le message « Ça marche ! » être affiché. Vous avez exécuté votre premier script Python !
III. Résolution éléments finis pour une poutre en traction▲
III-A. Problème, résolution éléments finis▲
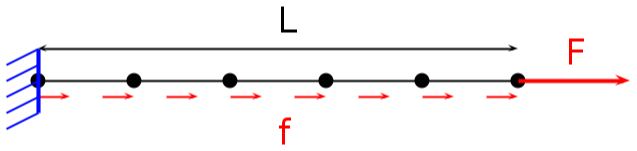
On s'intéresse au comportement d'une poutre console (encastrée à une extrémité) en traction de longueur L, de section S, de module de Young E soumise à une force F en bout de poutre et à une force linéique sur l'ensemble de la poutre de valeur f.
III-B. Formulation du problème▲
La théorie de la résistance des matériaux nous fournit les deux équations suivantes :
kitxmlcodelatexdvp\left\{\begin{matrix} \frac{dN}{dx}=-f \\ E\times S\times \frac{du}{dx}=N \\ \end{matrix}\right.finkitxmlcodelatexdvpavec :
- N l'effort normal dans la poutre ;
- u le déplacement longitudinal dû à la traction.
En combinant ces deux équations, on obtient :
kitxmlcodelatexdvpE\times S \times \frac{d^2u}{dx^2}=-ffinkitxmlcodelatexdvpCette équation différentielle peut être facilement résolue analytiquement (à la main). Dans le cadre général des problèmes d'élasticité 2D ou 3D, ce n'est pas possible. D'où la méthode d'approximation que sont les éléments finis.
III-C. Rappels sur la résolution éléments finis▲
En multipliant l'équation précédente par un champ test v et en l'intégrant sur la longueur de la poutre, on obtient :
kitxmlcodelatexdvp\int_0^L E\times S \times v \times \frac{d^2u}{dx^2} =-\int_0^L f \times vfinkitxmlcodelatexdvpEn intégrant par partie on obtient :
kitxmlcodelatexdvp[E\times S \times \frac{du}{dx} v]_0^L-\int_0^L E\times S \times \frac{du}{dx} \times \frac{dv}{dx} =-\int_0^L f \times vfinkitxmlcodelatexdvpOn impose à v d'être nul en L et 0, c'est-à-dire sur les bords du domaine. D'où :
kitxmlcodelatexdvp\int_0^L E\times S \times \frac{du}{dx} \times \frac{dv}{dx} =\int_0^L f \times vfinkitxmlcodelatexdvpC'est alors que l'on injecte l'approximation éléments finis :
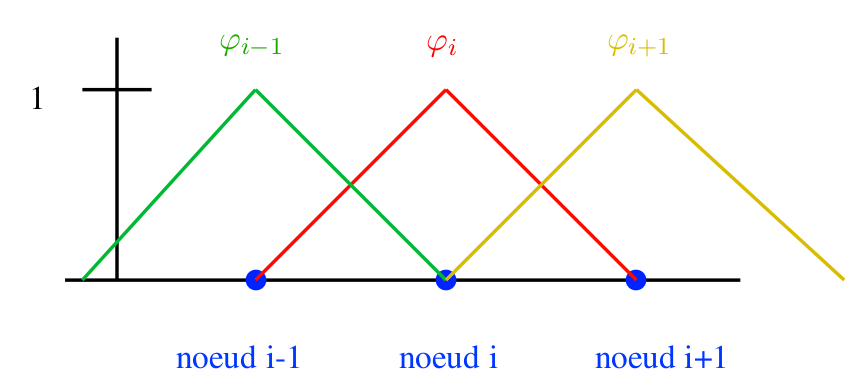
kitxmlcodelatexdvpu=\sum_{i=1}^{nn} \varphi_i u_i\ u= \begin{pmatrix} \varphi_1\cr \varphi_2\cr \vdots\cr \varphi_{nn}\cr \end{pmatrix} \begin{pmatrix} u_1 & u_2 & \dots & u_{nn} \end{pmatrix}finkitxmlcodelatexdvpavec nn le nombre de nœuds.
On choisit pour v :
kitxmlcodelatexdvpv=\sum_{i=1}^{nn} \varphi_i\ v= \begin{pmatrix} \varphi_1\cr \varphi_2\cr \vdots\cr \varphi_{nn}\cr \end{pmatrix}finkitxmlcodelatexdvpCe qui conduit à :
kitxmlcodelatexdvp\underbrace{ \int_0^L f \begin{pmatrix} \frac{d\varphi_1}{dx}\\ \frac{d\varphi_2}{dx}\\ \vdots\\ \frac{d\varphi_{nn}}{dx} \end{pmatrix} \begin{pmatrix} \frac{d\varphi_1}{dx} & \frac{d\varphi_2}{dx} & \cdots & \frac{d\varphi_{nn}}{dx} \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \\ \vdots \\ u_{nn} \end{pmatrix} }_\mathbb{K} = \underbrace{ \int_0^L f \begin{pmatrix} \varphi_1\\ \varphi_2\\ \vdots\\ \varphi_{nn} \end{pmatrix} }_{F}finkitxmlcodelatexdvpOn peut montrer que la construction de ces opérateurs peut se décomposer en l'addition de contribution des éléments à la rigidité du système et au vecteur force.
On a donc affaire à la résolution d'un système matriciel :
kitxmlcodelatexdvp\mathbb{K}u=FfinkitxmlcodelatexdvpVoilà pour la théorie, voyons comment coder cela en pratique !
IV. Implémentation en Python▲
Dans la suite, nous écrirons notre programme dans un fichier Python. Pour cela, ouvrez un nouveau fichier et enregistrez-le où vous le souhaitez.
IV-A. Chargement des paquets▲
Comme nous l'avons vu, Python fonctionne avec des bibliothèques d'outils regroupés en paquets (packages). Le langage en lui-même définit des éléments de base comme les boucles, les conditions, la gestion des variables et certaines structures de données comme les listes.
Pour résoudre un problème éléments finis, nous aurons besoin de manipuler des vecteurs et des matrices, et de tracer des graphiques pour visualiser les résultats. Pour cela nous utiliserons des paquets qui sont fournis avec les distributions qui ont été présentées précédemment.
Nous allons utiliser :
- numpy : un paquet définissant les matrices et vecteurs et permettant de les manipuler ;
- linalg, sous-paquet de numpy ;
- pyplot, sous-paquet de matplotlib, comme son nom l'indique une bibliothèque de tracé pour les maths.
Certains paquets peuvent en contenir d'autres, ce qui permet dans le cas de paquets volumineux de ne pas charger trop de fonctions dont on ne va pas se servir.
Pour importer un paquet, on utilise le mot-clé import.
Pour importer le paquet numpy on doit écrire :
import numpyTout simplement. Nous pouvons alors utiliser les outils de numpy par exemple la fonction identity en tapant :
numpy.identity(3)Écrivez ces lignes à la fin de votre script et exécutez-le. La console vous affiche le résultat :
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])La fonction numpy.identity crée une matrice identité (1 sur la diagonale, zéros ailleurs) de la taille passée en paramètre.
Pour appeler la fonction identity incluse dans le paquet numpy, il faut taper numpy.identity.
Comme nous risquons d'appeler plusieurs fonctions de ce paquet, il faudra à chaque fois les préfixer par numpy.. Pour ne pas avoir à faire cela, une solution consiste à modifier l'import du paquet en tapant :
from numpy import *On peut alors taper directement identity(3). Mais cette méthode pose un problème pour les grands projets où sont utilisés beaucoup de paquets. Deux paquets peuvent avoir chacun une fonction avec le même nom pour des utilisations radicalement différentes. On est alors plus trop sûr de quelle fonction va être appelée.
Une solution à mi-chemin est d'importer le paquet sous un nom raccourci :
import numpy as npIl faut alors taper np.identity(3). Cette solution garde l'avantage de savoir quel paquet on utilise sans pour autant alourdir trop le code. Nous garderons cette écriture pour la suite du projet.
Les autres paquets à inclure sont des sous-paquets. Pour cela :
from numpy import linalg as lg
from matplotlib import pyplot as pltPour résumer, voici à quoi doit ressembler votre script. Remarquez la ligne de commentaire, précédée d'un « # » pour commenter le code et le rendre plus sympa.
2.
3.
4.
5.
6.
7.
8.
9.
# -*- coding: utf-8 -*-
"""
@author: steven
"""
# Import des packages
import numpy as np
from numpy import linalg as lg
from matplotlib import pyplot as plt
IV-B. Mise en données▲
L'étape précédente était purement informatique, nous nous attaquons maintenant à la mise en données du problème avant sa résolution.
Dans chacune des étapes de la résolution, nous aurons besoin de connaître certaines grandeurs comme les paramètres matériau ou les dimensions de la poutre ou encore des paramètres de discrétisation.
2.
3.
4.
5.
6.
7.
# Paramètres
E = 200e9 # Module de Young
S = 0.01 # Section de la poutre
L = 1 # Longueur de la poutre
Fp = 1000 # Intensité de la force ponctuelle en Newtons
ne = 5 # Nombre d'éléments
fl = 500 # Intensité de la force linéique en Newtons/mètre
IV-C. Maillage▲
Un mailleur est un logiciel qui pour une géométrie en entrée crée un maillage et génère une table de connectivité et une table de coordonnées du maillage.
L'étape du maillage consiste donc à générer ces deux tables.
La table de coordonnées permet de connaître les coordonnées du nœud i du maillage.

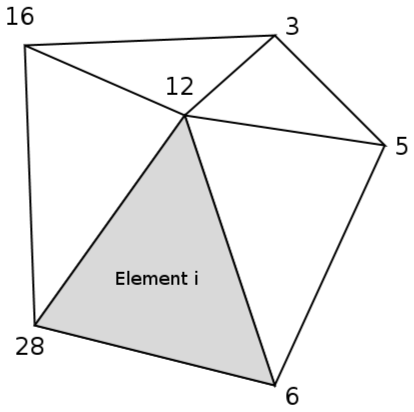
La table de connectivité permet, pour un élément i, de savoir comment est appelé dans le système global chacun de ces nœuds

Ces deux tables suffisent à définir complètement le maillage.
Dans notre cas, nous choisissons de numéroter comme suit :
Pour kitxmlcodeinlinelatexdvpn_efinkitxmlcodeinlinelatexdvp éléments, il y a donc kitxmlcodeinlinelatexdvpn_e+1finkitxmlcodeinlinelatexdvp nœuds.
La suite cherche donc à générer de manière automatique ces tables pour notre problème.
IV-C-1. Table de coordonnées▲
Dans notre cas, le problème est à une dimension. Une coordonnée d'un nœud est donc uniquement sa distance algébrique à l'origine.
Dans le cas où ne=5 et L=1, la table de coordonnées est :
La table est de taille (ne+1,1). Le plus simple est de partir d'une table de la bonne dimension remplie de 0 puis de la remplir case par case. Pour l'initialiser, on utilise la fonction np.zeros qui remplit exactement ce but. Pour lui indiquer la taille de la matrice à créer :
# Maillage
# Generation de la table coor
coor = np.zeros((ne+1,1)) # InitialisationPour ceux qui ont l'habitude de MATLAB, la différence est qu'il faut rajouter une paire de parenthèses. En effet, np.zeros ne prend qu'un seul paramètre.
Il faut maintenant peupler le vecteur qui pour l'instant est vide. Pour s'en convaincre, exécuter le script puis taper dans la console :
print (coor)Le plus simple pour remplir le vecteur est de parcourir les nœuds, et de remplir leur coordonnée dans le vecteur. Il faut donc parcourir ne+1 éléments, il est tout indiqué d'utiliser une boucle for qui aura ne+1 itérations, une pour chaque nœud. On cherche à faire prendre à une variable i les valeurs 1, 2, 3,…, ne+1. Nous irons insérer dans la i-ème case du vecteur la valeur kitxmlcodeinlinelatexdvp\frac{i-1}{ne}Lfinkitxmlcodeinlinelatexdvp
Pour générer une liste de valeur, on utilise la fonction range. Dans le terminal, tapez :
Python répond :
[0, 1, 2, 3, 4, 5]Or dans notre programme ne vaut 5 et nous voulions avoir la réponse :
[1, 2, 3, 4, 5, 6]En fait, Python a le mauvais goût, comme le C++ et d'autres langages, de compter à partir de 0, question de conventions.
De la même manière, pour accéder à la i-ème valeur du vecteur on appellera donc coor[i,0], 0 signifiant la première colonne.
La syntaxe de la boucle for en Python est la suivante :
2.
3.
4.
5.
6.
for variable in possibilites:
action 1
action 2
...
action n
action en dehors de la boucle
Notez bien les deux points « : » après avoir déclaré la condition de parcours des valeurs. Pour délimiter les actions qui vont être exécutées à chaque itération, il est obligatoire d'indenter (décaler vers la droite) le code. Pour cela il suffit d'appuyer sur la touche [TAB].
Nous voulions insérer dans la i-ème case la valeur kitxmlcodeinlinelatexdvp\frac{i-1}{ne}Lfinkitxmlcodeinlinelatexdvp, si i allait de 1 à ne+1. Or pour Python, i va de 0 à ne. Il faut alors insérer la valeur kitxmlcodeinlinelatexdvp\frac{i}{ne}Lfinkitxmlcodeinlinelatexdvp dans le vecteur (on a décalé de +1).
La boucle for qui fait prendre à une variable i ces valeurs s'écrit :
Pour calculer la valeur à insérer dans la i-ème case, on doit se servir de la valeur de i qui est un entier pour le diviser. Le problème est que pour Python, la division d'un entier donne un entier (division euclidienne). Pour le forcer à considérer i comme un réel, on lui convertit explicitement i en réel en appelant float(i).
IV-C-2. Table de connectivité▲
La table de connectivité se génère en parcourant les éléments cette fois et en listant le numéro des nœuds de l'élément dans le système global.
2.
3.
4.
5.
# Génération de la table connec
connec = np.zeros((ne,2))
for i in range(ne):
connec[i,0] = i+1
connec[i,1] = i+2
IV-D. Assemblage▲
Cette étape consiste à créer la matrice de rigidité et le vecteur force. Comme précédemment, on les initialise de la bonne taille à zéro puis on vient les remplir par les contributions de chaque élément.
K = np.zeros((ne+1,ne+1))
F = np.zeros((ne+1,1))On itère ensuite sur chaque élément grâce à une boucle for. On génère pour chaque élément sa matrice de rigidité élémentaire, dans notre cas de taille (2,2). Lors de l'assemblage, on « éclate » la matrice élémentaire entre kitxmlcodeinlinelatexdvpn_1finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpn_2finkitxmlcodeinlinelatexdvp, qui sont les numéros des nœuds de l'élément dans le système global, information que l'on trouve dans la table de connectivité.
La première chose à faire dans la boucle est de récupérer ces nombres n1 et n2 dans la table de connectivité, qui sont rangés à la ligne i.
2.
3.
4.
5.
6.
# Assemblage
K = np.zeros((ne+1,ne+1))
F = np.zeros((ne+1,1))
for i in range(ne):
n1 = connec[i,0]
n2 = connec[i,1]
On calcule ensuite la matrice de rigidité. Le seul paramètre qui change d'une matrice à l'autre est la longueur l de l'élément. Il faut la calculer, en allant chercher pour cela les coordonnées des nœuds de l'élément.
Comme Python compte à partir de 0, on décale nos valeurs de kitxmlcodeinlinelatexdvp-1finkitxmlcodeinlinelatexdvp. Par exemple, au lieu d'assigner kitxmlcodeinlinelatexdvpK[n1,n1]finkitxmlcodeinlinelatexdvp comme on le ferait sous MATLAB, on est obligé d'écrire kitxmlcodeinlinelatexdvpK[n1-1,n1-1]finkitxmlcodeinlinelatexdvp.
Pour l'assemblage de la force ponctuelle, chaque nœud reçoit la moitié de la force totale subie par la force surfacique.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
# Assemblage
K = np.zeros((ne+1,ne+1))
F = np.zeros((ne+1,1))
for i in range(ne):
n1 = connec[i,0]
n2 = connec[i,1]
l = abs(coor[n1-1,0]-coor[n2-1,0])
Ke = E*S/l * np.array([[1,-1],[-1,1]])
K[n1-1,n1-1] += Ke[0,0]
K[n2-1,n1-1] += Ke[1,0]
K[n1-1,n2-1] += Ke[0,1]
K[n2-1,n2-1] += Ke[1,1]
F[n1-1] += 0.5*fl*l
F[n2-1] += 0.5*fl*l
Remarquez que la syntaxe de Python pour incrémenter une variable selon le schéma kitxmlcodeinlinelatexdvpa=a+bfinkitxmlcodeinlinelatexdvp s'écrit kitxmlcodeinlinelatexdvpa+=bfinkitxmlcodeinlinelatexdvp, ce qui permet une écriture plus compacte.
Il ne faut pas oublier d'additionner la contribution de la force ponctuelle, qui s'ajoute au dernier nœud.
# Ajout de la force ponctuelle
F[ne] += FpIV-E. Prise en compte des conditions limites▲
Il faut maintenant imposer le déplacement à certains nœuds. On sépare, quitte à réorganiser la matrice de rigidité les déplacements connus kitxmlcodeinlinelatexdvpu_cfinkitxmlcodeinlinelatexdvp et inconnus kitxmlcodeinlinelatexdvpu_ifinkitxmlcodeinlinelatexdvp. Le problème s'écrit alors :
kitxmlcodelatexdvp\begin{pmatrix} K_{ii} & K_{ic} \cr K_{ci} & K_{cc} \cr \end{pmatrix} \begin{pmatrix} u_i \cr u_c \end{pmatrix}= \begin{pmatrix} F_i \cr F_c \end{pmatrix}finkitxmlcodelatexdvpSi on ne garde que la première ligne du système :
kitxmlcodelatexdvpK_{ii}u_i+K_{ic} u_c=F_ifinkitxmlcodelatexdvpD'où :
kitxmlcodelatexdvpu_i=K_{ii}^{-1}(F_i-K_{ic} u_c)finkitxmlcodelatexdvpDans notre exemple, kitxmlcodeinlinelatexdvpu_cfinkitxmlcodeinlinelatexdvp est réduit à un seul élément, kitxmlcodeinlinelatexdvpu_1finkitxmlcodeinlinelatexdvp, déplacement du premier nœud et égal à 0. Dans ce cas particulier, l'expression devient :
kitxmlcodelatexdvpu_i=K_{ii}^{-1}(F_i)finkitxmlcodelatexdvpPour obtenir kitxmlcodeinlinelatexdvpK_{ii}finkitxmlcodeinlinelatexdvp, il faut supprimer la première ligne et première colonne de kitxmlcodeinlinelatexdvpKfinkitxmlcodeinlinelatexdvp et pour kitxmlcodeinlinelatexdvpF_ifinkitxmlcodeinlinelatexdvp, supprimer le premier élément de kitxmlcodeinlinelatexdvpFfinkitxmlcodeinlinelatexdvp. Ceci s'écrit grâce à la fonction np.delete.
Elle prend respectivement comme paramètre :
- la matrice ou le vecteur à partir duquel la fonction va travailler ;
- la place de l'élément à supprimer. Ici les premières lignes ou colonnes donc 1, donc 0 en convention Python ;
- 0 si c'est une ligne à supprimer, 1 si c'est une colonne.
Il est important de remarquer que la fonction ne modifie pas la matrice ou le vecteur passé en paramètre. Elle le copie, effectue les opérations demandées et renvoie le résultat. C'est pour cela qu'il faut assigner ce résultat :
2.
3.
4.
# Prise en compte des CL
Kii = np.delete(K,0,0)
Kii = np.delete(Kii,0,1)
Fi = np.delete(F,0,0)
Cette série d'instructions réalise :
- copier kitxmlcodeinlinelatexdvpKfinkitxmlcodeinlinelatexdvp et supprimer dans cette copie la première ligne. Assigner le résultat dans une nouvelle variable kitxmlcodeinlinelatexdvpK_{ii}finkitxmlcodeinlinelatexdvp. Il faut remarquer que K n'a donc pas été modifié !
- copier kitxmlcodeinlinelatexdvpK_{ii}finkitxmlcodeinlinelatexdvp, supprimer dans cette copie la première colonne. Assigner le résultat dans kitxmlcodeinlinelatexdvpK_{ii}finkitxmlcodeinlinelatexdvp pour le mettre à jour ;
- copier kitxmlcodeinlinelatexdvpFfinkitxmlcodeinlinelatexdvp, supprimer dans cette copie la première ligne. Assigner le résultat dans kitxmlcodeinlinelatexdvpF_{i}finkitxmlcodeinlinelatexdvp pour le mettre à jour.
IV-F. Vérification de la construction des matrices et vecteurs▲
Nous avons effectué des opérations relativement complexes sur des matrices et vecteurs, et on peut rapidement se tromper surtout quand on débute dans un nouveau langage. Pour vérifier les opérations effectuées, on peut vouloir afficher une matrice ou un vecteur par exemple kitxmlcodeinlinelatexdvpK_{ii}finkitxmlcodeinlinelatexdvp. La manière simple est de taper dans la console ou d'écrire à la fin du script :
print (Kii)La réponse en console est du genre :
2.
3.
4.
5.
6.
7.
8.
9.
10.
[[ 2.00000000e+10 -1.00000000e+10 0.00000000e+00 0.00000000e+00
0.00000000e+00]
[ -1.00000000e+10 2.00000000e+10 -1.00000000e+10 0.00000000e+00
0.00000000e+00]
[ 0.00000000e+00 -1.00000000e+10 2.00000000e+10 -1.00000000e+10
0.00000000e+00]
[ 0.00000000e+00 0.00000000e+00 -1.00000000e+10 2.00000000e+10
-1.00000000e+10]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00 -1.00000000e+10
1.00000000e+10]]
Ce qui n'est pas très visuel. Si vous changez en haut du script ne=20 par exemple, le résultat sera une bouillie de nombres…
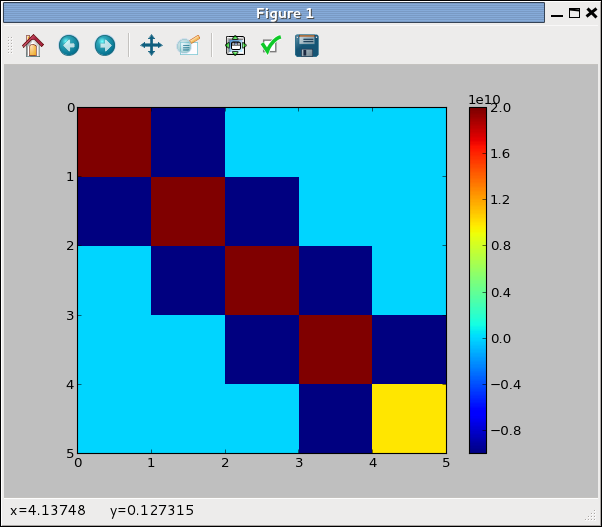
C'est pourquoi je vous propose de taper ces lignes après les opérations sur kitxmlcodeinlinelatexdvpK_{ii}finkitxmlcodeinlinelatexdvp notamment :
2.
3.
4.
plt.figure()
plt.pcolor(Kii)
plt.gca().invert_yaxis()
plt.colorbar()
Vous avez alors une visualisation de la matrice, les nombres étant transformés en couleurs.
IV-G. Résolution de système linéaire▲
Finalement, la résolution du système linéaire tient en une seule ligne :
ui = lg.solve(Kii,Fi)IV-H. Posttraitement▲
Nous avons obtenu les kitxmlcodeinlinelatexdvpu_ifinkitxmlcodeinlinelatexdvp par calcul. Il faut maintenant réintégrer les kitxmlcodeinlinelatexdvpu_cfinkitxmlcodeinlinelatexdvp pour former kitxmlcodeinlinelatexdvpufinkitxmlcodeinlinelatexdvp :
u = np.insert(ui,0,0)
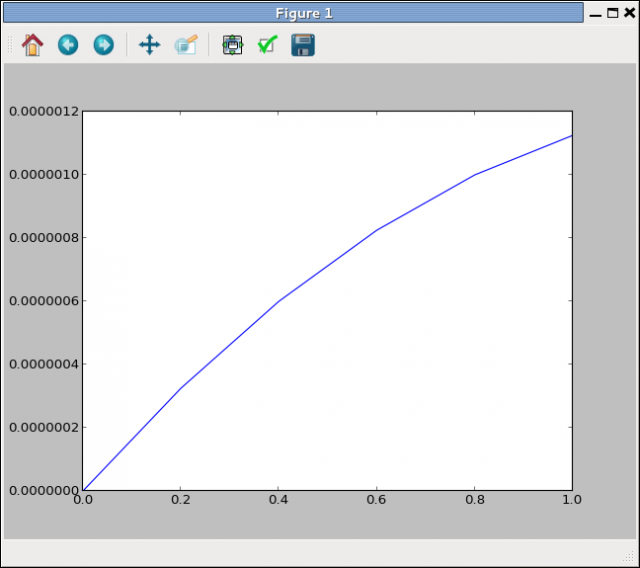
plt.plot(coor,u)L'instruction plot permet de tracer la courbe, en prenant le premier vecteur comme valeurs sur x, le deuxième sur y.
Nous obtenons alors le déplacement en fonction de la coordonnée des nœuds.
Maintenant que l'on a un code éléments finis qui donne des résultats qui semblent cohérents, on cherche à comparer le déplacement obtenu avec le déplacement analytique. En effet, en programmation, il est obligatoire de vérifier le bon fonctionnement du code en essayant sur un cas test dont on connaît à l'avance le résultat.
La première équation donnée par la RDM permet la résolution de l'effort normal :
kitxmlcodelatexdvpN(x)=-fx+c_1finkitxmlcodelatexdvpOr en bout de poutre, kitxmlcodeinlinelatexdvpN(L)=Ffinkitxmlcodeinlinelatexdvp, d'où
kitxmlcodelatexdvpN(x)=F(l-x)finkitxmlcodelatexdvpLa relation de comportement nous donne le déplacement :
kitxmlcodelatexdvpu(x)=\frac{1}{ES}(Fx-\frac{f(L-x)^2}{2}+c_2)finkitxmlcodelatexdvpOr kitxmlcodeinlinelatexdvpu(0)=0finkitxmlcodeinlinelatexdvp, d'où :
kitxmlcodelatexdvpu(x)=\frac{1}{ES}(Fx+fLx-f\frac{x^2}{2}) finkitxmlcodelatexdvpNous voulons donc tracer sur un même graphique le déplacement éléments finis et le déplacement analytique. Nous n'allons pas tracer cette fonction de manière exacte, nous allons l'évaluer en un certain nombre de points. Pour cela on se donne pour x un nombre fini de valeurs grâce à la fonction linspace, qui retourne un vecteur de valeurs régulièrement espacées en donnant la valeur de début, de fin et le nombre de valeurs.
x = np.linspace(0,L,num=100)Nous pouvons alors écrire la formule de uth en utilisant le x ainsi défini. On le trace en superposition avec la solution éléments finis avec une légende pour distinguer les deux courbes avec le code suivant :
2.
3.
4.
5.
uth = 1/(E*S)*((Fp+fl*L)*x-fl*np.square(x)/2)
plt.figure()
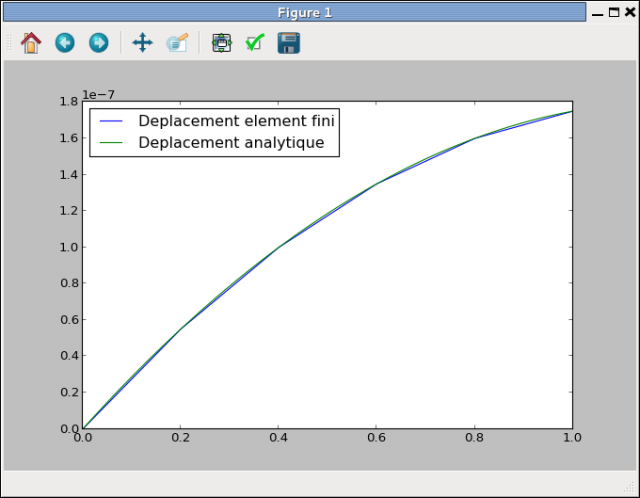
plt.plot(coor,u,x,uth)
plt.legend(('Deplacement EF','Deplacement analytique'),loc=2)
Il n'est pas possible de mettre tous les éléments d'un vecteur au carré en tapant x^2 comme cela se fait pour les réels. On utilise alors la fonction np.square.
Les deux courbes se superposent, on valide ainsi le calcul éléments finis. On peut remarquer que le résultat est exact à l'endroit où sont positionnés les nœuds. Entre ceux-ci, on a postulé avec l'approximation éléments finis que le déplacement était linéaire, or la résolution analytique nous montre qu'elle est quadratique. On ne peut donc pas représenter convenablement entre les nœuds la solution.
Le code ainsi créé est une suite d'instructions simples qui travaillent directement sur les variables pour arriver au résultat. Cette technique de programmation est intuitive, mais devient rapidement complexe lorsque l'on veut empiler les fonctionnalités. Nous pourrions par exemple vouloir que l'utilisateur puisse définir de manière plus complexe le chargement ou les conditions aux limites. Nous présenterons dans un autre cours une manière différente d'envisager la manière de coder pour permettre d'avoir un code bien plus maintenable et modulaire.
V. Version finale du code▲
Pour récapituler, voici la version complète du code :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
# -*- coding: utf-8 -*-
"""
@author: steven
"""
# Import des packages
import numpy as np
from numpy import linalg as lg
from matplotlib import pyplot as plt
# Paramètres
E = 200e9 #Module de young
S = 0.01 # Section de la poutre
L = 1 # Longueur de la poutre
Fp = 1000 # Intensité de la force ponctuelle en Newtons
ne = 5 # Nombre d'éléments
fl = 500 # Intensité de la force linéique en Newtons/mètre
# Maillage
# Génération de la table coor
coor = np.zeros((ne+1,1)) # Initialisation
for i in range(ne+1): # Parcours des nœuds
coor[i,0] = (float(i)/(ne))*L
#print (coor)
# Génération de la table connec
connec = np.zeros((ne,2))
for i in range(ne):
connec[i,0] = i+1
connec[i,1] = i+2
# Assemblage
K = np.zeros((ne+1,ne+1))
F = np.zeros((ne+1,1))
for i in range(ne):
n1 = connec[i,0]
n2 = connec[i,1]
l = abs(coor[n1-1,0]-coor[n2-1,0])
Ke = E*S/l*np.array([[1,-1],[-1,1]])
K[n1-1,n1-1] += Ke[0,0]
K[n2-1,n1-1] += Ke[1,0]
K[n1-1,n2-1] += Ke[0,1]
K[n2-1,n2-1] += Ke[1,1]
F[n1-1] += 0.5*fl*l
F[n2-1] += 0.5*fl*l
# Ajout de la force ponctuelle
F[ne] += Fp
# Prise en compte des CL
Kii = np.delete(K,0,0)
Kii = np.delete(Kii,0,1)
Fi = np.delete(F,0,0)
#plt.figure()
#plt.pcolor(Kii)
#plt.gca().invert_yaxis()
#plt.colorbar()
# Résolution
ui = lg.solve(Kii,Fi)
# On remet l'élément supprimé
u = np.insert(ui,0,0)
x = np.linspace(0,L,num=100)
uth = 1/(E*S)*((Fp+fl*L)*x-fl*np.square(x)/2)
plt.figure()
plt.plot(coor,u,x,uth)
plt.legend(('Deplacement element fini', 'Deplacement analytique'), loc=2)
VI. Note de la rédaction de Developpez.com ▲
Nous tenons à remercier Winjerome par la mise au gabarit, f-leb pour la mise à jour et Claude Leloup pour la relecture orthographique.