Tutoriel Matplotlib

Matplotlib est probablement l'un des packages Python les plus utilisés pour la représentation de graphiques en 2D. Il fournit aussi bien un moyen rapide de visualiser des données grâce au langage Python, que des illustrations de grande qualité dans divers formats.

3 commentaires

Article lu fois.

Les deux auteur et traducteur

Nicolas P. Rougier

Traducteur : Raphaël Seban

L'article

Publié le 11 juillet 2014 - Mis à jour le 29 avril 2020

Version PDF Version hors-ligne

ePub, Azw et Mobi

Liens sociaux

I. Présentation▲

Nous explorerons matplotlib en console interactive et nous tenterons d'aborder les cas les plus courants.

I-A. IPython et le mode pylab▲

IPython est une console interactive Python améliorée qui supporte un grand nombre de fonctionnalités très intéressantes parmi lesquelles les entrées/sorties nommées, l'utilisation directe de commandes shell, un système de débogage amélioré et bien plus encore.

En lançant cette console avec l'argument -pylab (--pylab depuis IPython version 0.12), l'on dispose immédiatement d'une session matplotlib interactive avec de nombreuses fonctionnalités du type Matlab™ / Mathematica™.

I-B. Pylab▲

Pylab fournit une interface procédurale à la librairie graphique matplotlib orientée objet. Elle est basée sur un modèle très proche de Matlab™. De la sorte, la grande majorité des commandes pylab ont leur équivalent Matlab™ avec des arguments similaires. Les commandes les plus importantes sont expliquées avec des exemples en console interactive.

II. Graphique simple▲

Dans cette rubrique, nous voudrions tracer les fonctions sinus et cosinus sur un seul et même graphique. En partant des paramètres par défaut, nous allons améliorer la représentation étape par étape jusqu'à obtenir quelque chose de correct.

Tout d'abord, récupérons les données des fonctions sinus et cosinus :

Sélectionnez

from pylab import *

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

X est désormais un tableau numpy comprenant 256 valeurs allant de -? à +? (inclus). C et S représentent respectivement le cosinus et le sinus de ces valeurs.

Pour tester cet exemple, vous pouvez lancer une console interactive IPython :

Sélectionnez

$ ipython --pylab

Vous obtiendrez alors un message de bienvenue ressemblant à ceci :

Sélectionnez

IPython 0.13 -- An enhanced Interactive Python.
? -> Introduction to IPython's features.
%magic -> Information about IPython's 'magic' % functions.
help -> Python's own help system.
object? -> Details about 'object'. ?object also works, ?? prints more.

Welcome to pylab, a matplotlib-based Python environment.
For more information, type 'help(pylab)'.

Vous pouvez aussi copier/coller le code source de chaque exemple dans un fichier et le lancer comme un script Python ordinaire, exemple :

Sélectionnez

$ python exercice_1.py

Le code source des exercices (exercice_xx.py, …) est dissimulé par défaut. Cliquez sur l'image Image non disponible pour le faire apparaître à chaque étape.

II-A. Paramètres par défaut▲

Documentation

exercice_1.py

Cacher/Afficher le codeSélectionnez

from pylab import *

n = 256
X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)
plot(X,C),plot(X,S)

#savefig("../figures/exercice_1.png",dpi=72)
show()

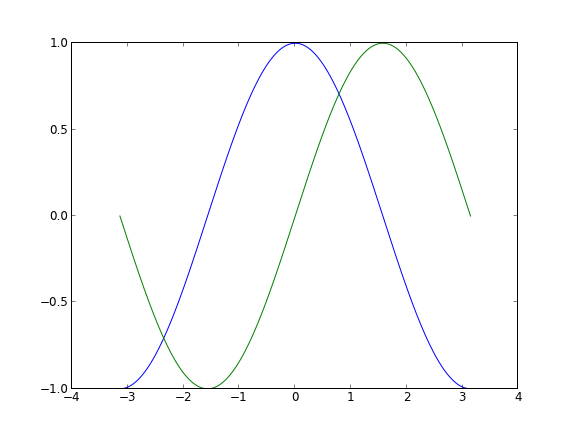
Matplotlib est fournie avec un jeu de paramètres par défaut qui permet de personnaliser toute sorte de propriétés. Vous pouvez contrôler les réglages par défaut de (presque) toutes les propriétés : taille du graphique, résolution en points par pouce (dpi), épaisseur du trait, couleurs, styles, vues, repères, grilles, textes, polices de caractères, etc. Bien que les réglages par défaut répondent à la plupart des cas courants, vous pourriez être amenés à en modifier quelques-uns pour des cas plus spécifiques.

Sélectionnez

from pylab import *

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plot(X,C)
plot(X,S)

show()

II-B. Modifier les réglages par défaut▲

Documentation

Personnaliser matplotlib

exercice_2.py

Cacher/Afficher le codeSélectionnez

# Import everything from matplotlib (numpy is accessible via 'np' alias)
from pylab import *

# Create a new figure of size 8x6 inches, using 80 dots per inch
figure(figsize=(8,6), dpi=80)

# Create a new subplot from a grid of 1x1
subplot(111)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

# Plot cosine using blue color with a continuous line of width 1 (pixels)
plot(X, C, color="blue", linewidth=1.0, linestyle="-")

# Plot sine using green color with a continuous line of width 1 (pixels)
plot(X, S, color="green", linewidth=1.0, linestyle="-")

# Set x limits
xlim(-4.0,4.0)

# Set x ticks
xticks(np.linspace(-4,4,9,endpoint=True))

# Set y limits
ylim(-1.0,1.0)

# Set y ticks
yticks(np.linspace(-1,1,5,endpoint=True))

# Save figure using 72 dots per inch
# savefig("../figures/exercice_2.png",dpi=72)

# Show result on screen
show()

Dans le script suivant, nous modifions (et commentons) les réglages qui impactent directement l'apparence du graphique.

Ces réglages ont été volontairement redéfinis à leurs valeurs par défaut, mais vous pouvez les faire varier pour voir ce que cela donne (voir les rubriques Propriétés de lignePropriétés de trait et Styles de traitStyles de trait plus bas, rubrique Références).

Sélectionnez

# on importe tout de matplotlib
# numpy est accessible via l'alias 'np'
from pylab import *

# on crée un graphique de 8x6 pouces 
# avec une résolution de 80 points par pouce
figure(figsize=(8,6), dpi=80)

# on crée une nouvelle vue dans une grille de 1 ligne x 1 colonne
subplot(1,1,1)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

# on trace la fonction cosinus en bleu avec un trait plein de 1 pixel d'épaisseur
plot(X, C, color="blue", linewidth=1.0, linestyle="-")

# on trace la fonction sinus en vert avec un trait plein de 1 pixel d'épaisseur
plot(X, S, color="green", linewidth=1.0, linestyle="-")

# limites de l'axe (O,x) des abscisses
xlim(-4.0,4.0)

# graduations de l'axe (O,x) des abscisses
xticks(np.linspace(-4,4,9,endpoint=True))

# limites de l'axe (O,y) des ordonnées
ylim(-1.0,1.0)

# graduations de l'axe (O,y) des ordonnées
yticks(np.linspace(-1,1,5,endpoint=True))

# on enregistre le graphique avec une résolution de 72 points par pouce
# savefig("exercice_2.png",dpi=72)

# on affiche le résultat à l'écran
show()

II-C. Modifier les couleurs et épaisseurs de trait▲

Documentation

exercice3.py

Cacher/Afficher le codeSélectionnez

from pylab import *

figure(figsize=(8,5), dpi=80)
subplot(111)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plot(X, C, color="blue", linewidth=2.5, linestyle="-")
plot(X, S, color="red", linewidth=2.5, linestyle="-")

xlim(-4.0,4.0)
xticks(np.linspace(-4,4,9,endpoint=True))

ylim(-1.0,1.0)
yticks(np.linspace(-1,1,5,endpoint=True))

#savefig("../figures/exercice_3.png",dpi=72)
show()

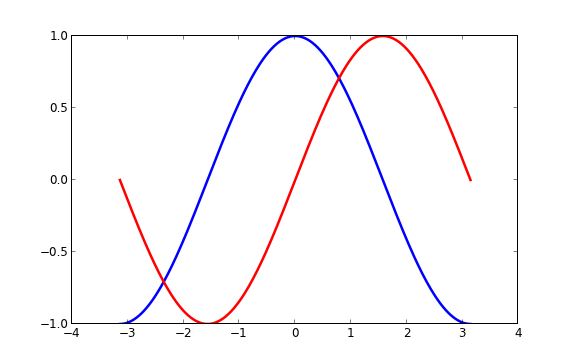
Pour commencer, nous voudrions mettre la courbe cosinus en bleu, la courbe sinus en rouge et épaissir un peu le trait des deux courbes. Nous modifierons aussi, très légèrement, la taille du graphique afin que ce dernier paraisse plus horizontal, plus panoramique.

Sélectionnez

...
figure(figsize=(10,6), dpi=80)
plot(X, C, color="blue", linewidth=2.5, linestyle="-")
plot(X, S, color="red",  linewidth=2.5, linestyle="-")
...

II-D. Délimiter les axes du repère▲

Documentation

exercice_4.py

Cacher/Afficher le codeSélectionnez

from pylab import *

figure(figsize=(8,5), dpi=80)
subplot(111)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plot(X, C, color="blue", linewidth=2.5, linestyle="-")
plot(X, S, color="red", linewidth=2.5, linestyle="-")

xlim(X.min()*1.1, X.max()*1.1)
ylim(C.min()*1.1,C.max()*1.1)

# savefig("../figures/exercice_4.png",dpi=72)
show()

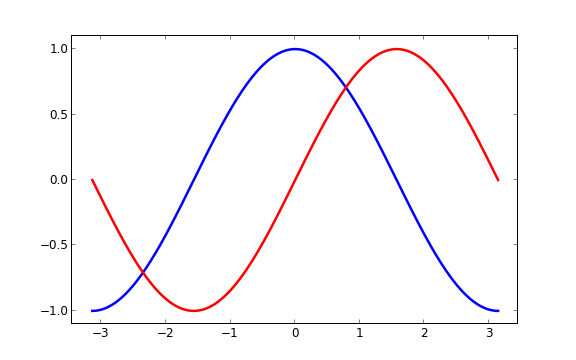
Les limites actuelles sur les axes du repère sont un peu trop serrées, nous voudrions les agrandir afin d'aérer le graphique.

Sélectionnez

...
xlim(X.min()*1.1, X.max()*1.1)
ylim(C.min()*1.1, C.max()*1.1)
...

Notez que pour une version plus robuste, nous devrions plutôt écrire :

Sélectionnez

xmin ,xmax = X.min(), X.max()
ymin, ymax = Y.min(), Y.max()

dx = (xmax - xmin) * 0.2
dy = (ymax - ymin) * 0.2

xlim(xmin - dx, xmax + dx)
ylim(ymin - dy, ymax + dy)

II-E. Définir les graduations▲

Documentation

exercice_5.py

Cacher/Afficher le codeSélectionnez

from pylab import *

figure(figsize=(8,5), dpi=80)
subplot(111)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plot(X, C, color="blue", linewidth=2.5, linestyle="-")
plot(X, S, color="red", linewidth=2.5, linestyle="-")

xlim(X.min()*1.1, X.max()*1.1)
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])

ylim(C.min()*1.1,C.max()*1.1)
yticks([-1, 0, +1])

# savefig("../figures/exercice_5.png",dpi=72)
show()

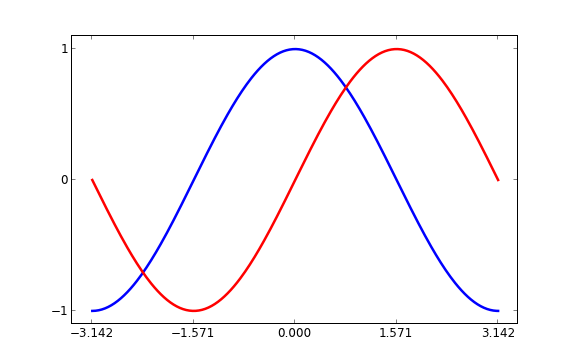
Les graduations actuelles ne sont pas idéales : elles n'affichent pas les valeurs (+/-?, +/-?/2) qui nous intéressent pour sinus et cosinus. Modifions-les pour qu'elles correspondent à ces valeurs.

Sélectionnez

...
xticks( [-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
yticks([-1, 0, +1])
...

II-F. Définir le texte des graduations▲

Documentation

exercice_6.py

Cacher/Afficher le codeSélectionnez

from pylab import *

figure(figsize=(8,5), dpi=80)
subplot(111)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plot(X, C, color="blue", linewidth=2.5, linestyle="-")
plot(X, S, color="red", linewidth=2.5, linestyle="-")

xlim(X.min()*1.1, X.max()*1.1)
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])

ylim(C.min()*1.1,C.max()*1.1)
yticks([-1, 0, +1],
       [r'$-1$', r'$0$', r'$+1$'])

# savefig("../figures/exercice_6.png",dpi=72)
show()

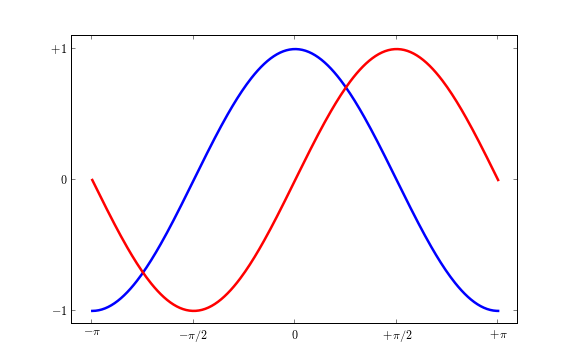
Les graduations sont bien placées, mais le contenu de leur texte n'est pas très explicite. Nous pourrions deviner que 3.142 correspond à Pi, mais ce serait beaucoup mieux de l'indiquer clairement. Lorsqu'on définit des valeurs pour les graduations, il est aussi possible de définir des étiquettes de texte correspondant à ces valeurs dans une liste fournie en second argument d'appel de fonction. Nous utiliserons une notation LaTeX pour obtenir un meilleur rendu final.

Sélectionnez

...
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])

yticks([-1, 0, +1],
       [r'$-1$', r'$0$', r'$+1$'])
...

II-G. Déplacer les axes du repère▲

Documentation

exercice_7.py

Cacher/Afficher le codeSélectionnez

from pylab import *

figure(figsize=(8,5), dpi=80)
subplot(111)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plot(X, C, color="blue", linewidth=2.5, linestyle="-")
plot(X, S, color="red", linewidth=2.5, linestyle="-")

ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

xlim(X.min()*1.1, X.max()*1.1)
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])

ylim(C.min()*1.1,C.max()*1.1)
yticks([-1, 0, +1],
       [r'$-1$', r'$0$', r'$+1$'])

# savefig("../figures/exercice_7.png",dpi=72)
show()

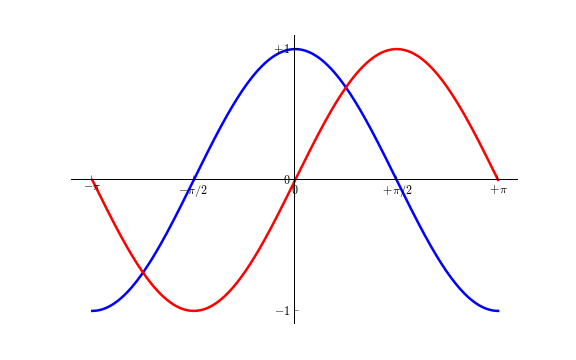
Les axes du repère sont les droites qui portent les marques de graduation et qui délimitent la zone de représentation du graphique. Ces axes peuvent être placés arbitrairement. Jusqu'à présent, ils étaient sur les bords extérieurs du graphique. Déplaçons-les de telle sorte qu'ils se croisent au centre du graphique. Comme nous avons quatre droites pour le moment, nous en masquerons deux en définissant leur couleur à None et nous déplacerons les deux autres vers le point d'origine de coordonnées (0, 0) dans l'espace de coordonnées nommé 'data'.

Sélectionnez

...
ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
...

II-H. Ajouter une légende au graphique▲

Documentation

exercice_8.py

Cacher/Afficher le codeSélectionnez

from pylab import *

figure(figsize=(8,5), dpi=80)
subplot(111)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plot(X, S, color="red", linewidth=2.5, linestyle="-",  label="sine")

ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

xlim(X.min()*1.1, X.max()*1.1)
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])

ylim(C.min()*1.1,C.max()*1.1)
yticks([-1, +1],
       [r'$-1$', r'$+1$'])


legend(loc='upper left')

# savefig("../figures/exercice_8.png",dpi=72)
show()

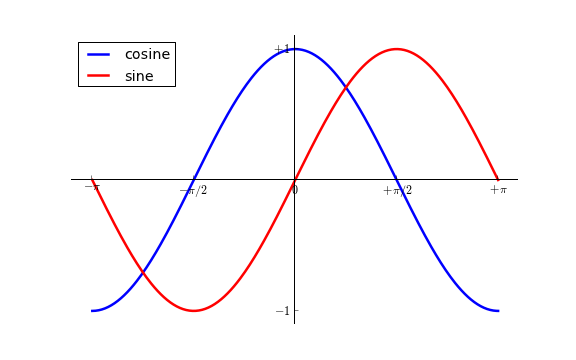
À présent, ajoutons au graphique une légende dans le coin supérieur gauche. Pour ce faire, il suffit d'ajouter l'argument nommé 'label="texte"' à la commande plot(), puis de spécifier l'emplacement de cette légende.

Sélectionnez

...
plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plot(X, S, color="red",  linewidth=2.5, linestyle="-", label="sine")

legend(loc='upper left')
...

II-I. Annoter certains points remarquables▲

Documentation

exercice_9.py

Cacher/Afficher le codeSélectionnez

from pylab import *

figure(figsize=(8,5), dpi=80)
subplot(111)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plot(X, S, color="red", linewidth=2.5, linestyle="-",  label="sine")

ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

xlim(X.min()*1.1, X.max()*1.1)
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])

ylim(C.min()*1.1,C.max()*1.1)
yticks([-1, +1],
       [r'$-1$', r'$+1$'])

t = 2*np.pi/3
plot([t,t],[0,np.cos(t)],
     color ='blue',  linewidth=1.5, linestyle="--")
scatter([t,],[np.cos(t),], 50, color ='blue')
annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$', xy=(t, np.sin(t)),  xycoords='data',
         xytext=(+10, +30), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

plot([t,t],[0,np.sin(t)],
          color ='red',  linewidth=1.5, linestyle="--")
scatter([t,],[np.sin(t),], 50, color ='red')
annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$', xy=(t, np.cos(t)),  xycoords='data',
         xytext=(-90, -50), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

legend(loc='upper left')

# savefig("../figures/exercice_9.png",dpi=72)
show()

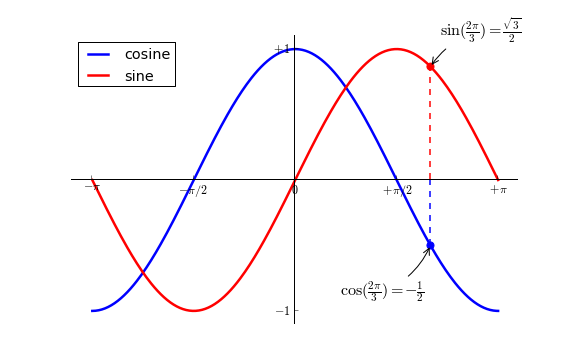
Annotons quelques points remarquables avec la commande annotate(). Nous choisirons la valeur x=2?/3 aussi bien pour la courbe sinus que pour la courbe cosinus. Nous placerons tout d'abord une marque sur la courbe (gros point rond), puis nous tracerons une ligne en pointillé pour relier cette marque à l'axe (O,x) des abscisses. Pour finir, nous utiliserons la commande annotate() pour afficher du texte et une flèche d'indication.

Sélectionnez

...

t = 2*np.pi/3
plot([t,t],[0,np.cos(t)], color ='blue', linewidth=2.5, linestyle="--")
scatter([t,],[np.cos(t),], 50, color ='blue')

annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',
         xy=(t, np.sin(t)), xycoords='data',
         xytext=(+10, +30), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

plot([t,t],[0,np.sin(t)], color ='red', linewidth=2.5, linestyle="--")
scatter([t,],[np.sin(t),], 50, color ='red')

annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$',
         xy=(t, np.cos(t)), xycoords='data',
         xytext=(-90, -50), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
...

II-J. Le diable se cache toujours dans les détails▲

Documentation

exercice_10.py

Cacher/Afficher le codeSélectionnez

from pylab import *

figure(figsize=(8,5), dpi=80)
subplot(111)

X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)

plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plot(X, S, color="red", linewidth=2.5, linestyle="-",  label="sine")

ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

xlim(X.min()*1.1, X.max()*1.1)
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
       [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])

ylim(C.min()*1.1,C.max()*1.1)
yticks([-1, +1],
       [r'$-1$', r'$+1$'])


legend(loc='upper left')

t = 2*np.pi/3
plot([t,t],[0,np.cos(t)],
     color ='blue',  linewidth=1.5, linestyle="--")
scatter([t,],[np.cos(t),], 50, color ='blue')
annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$', xy=(t, np.sin(t)),  xycoords='data',
         xytext=(+10, +30), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

plot([t,t],[0,np.sin(t)],
          color ='red',  linewidth=1.5, linestyle="--")
scatter([t,],[np.sin(t),], 50, color ='red')
annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$', xy=(t, np.cos(t)),  xycoords='data',
         xytext=(-90, -50), textcoords='offset points', fontsize=16,
         arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

for label in ax.get_xticklabels() + ax.get_yticklabels():
    label.set_fontsize(16)
    label.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.65 ))


# savefig("../figures/exercice_10.png",dpi=72)
show()

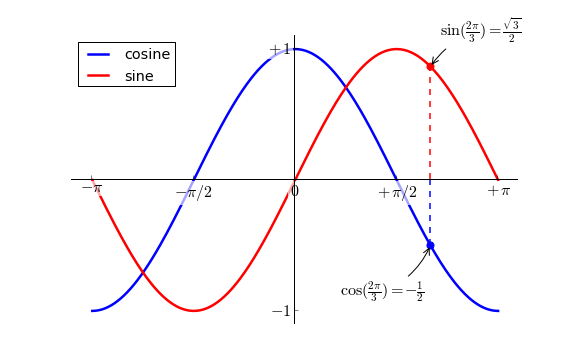
Comme vous pouvez le remarquer, les étiquettes des graduations sont un peu difficiles à lire. Nous pourrions les agrandir, puis ajuster leurs propriétés de telle sorte qu'elles s'affichent sur un ruban blanc semi-transparent, cela nous permettrait de mieux visualiser aussi bien la courbe que les étiquettes.

Sélectionnez

...
for label in ax.get_xticklabels() + ax.get_yticklabels():
    label.set_fontsize(16)
    label.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.65 ))
...

III. Graphiques, vues en grille, vues libres et graduations▲

Jusqu'à présent, nous avons surtout utilisé la création de graphiques et de vues par défaut. Tout cela est bien pratique lorsque l'on souhaite obtenir un résultat rapide, mais nous pourrions avoir un contrôle plus fin sur le résultat en utilisant explicitement les graphiques (matplotlib.figure), les vues en grille (matplotlib.subplot) et les vues libres (matplotlib.axes). Dans matplotlib, un objet figure représente la fenêtre GUI dans son ensemble. À l'intérieur de cette fenêtre, plusieurs types d'affichage peuvent figurer. Alors qu'une vue en grille (subplot) positionne les tracés à l'intérieur d'une grille d'affichage, les vues libres (axes) autorisent un placement plus arbitraire au sein de l'objet figure. Les deux peuvent être très utiles selon l'usage que l'on veut en faire. Nous avons d'ores et déjà travaillé avec des graphiques (figures) et des vues en grille (subplots) sans les mentionner explicitement. Lorsque nous utilisons la commande plot(), matplotlib appelle gca() pour obtenir les vues libres actuelles et gca() appelle à son tour gcf() pour obtenir l'objet figure (graphique) actuel. S'il n'y a pas d'objet figure à ce moment-là, gcf() appelle figure() pour en créer un nouveau ou plus précisément, pour créer un objet figure contenant une vue en grille subplot(1,1,1). Voyons tout cela en détail.

III-A. Graphiques (mathplotlib.figure)▲

Un objet figure (graphique) représente la fenêtre GUI intitulée « Figure #nnn » avec nnn le numéro de la figure. Les fenêtres « figure » sont numérotées à partir de 1 et non pas à partir de zéro (0) comme pour le comptage en Python. Cela est clairement conforme au style Matlab™. Plusieurs arguments nommés déterminent l'apparence d'un objet figure :

Argument	Valeur par défaut	Description
num	1	numéro de l'objet figure
figsize	figure.figsize	taille en pouces (largeur, hauteur)
dpi	figure.dpi	résolution en points par pouce
facecolor	figure.facecolor	couleur d'arrière-plan
edgecolor	figure.edgecolor	couleur de la bordure entourant l'arrière-plan
frameon	True	dessiner le cadre de l'objet figure ou non

Les valeurs par défaut peuvent être spécifiées dans un fichier de ressources. Elles sont utilisées la plupart du temps. Seul le numéro de figure est fréquemment changé.

Lorsque vous travaillez avec la fenêtre GUI, vous pouvez la fermer soit avec le bouton « x » dédié, soit par le code avec la commande close().

Selon le cas :

close() ferme uniquement l'objet figure actif ;
close(num) ferme l'objet figure numéro num ;
close(fig) ferme l'objet figure référencé par fig ;
close('all') ferme tous les objets figure actuellement actifs.

Comme pour tous les autres objets, vous pouvez définir les propriétés d'un objet figure avec les méthodes set_<nom propriété>(value).

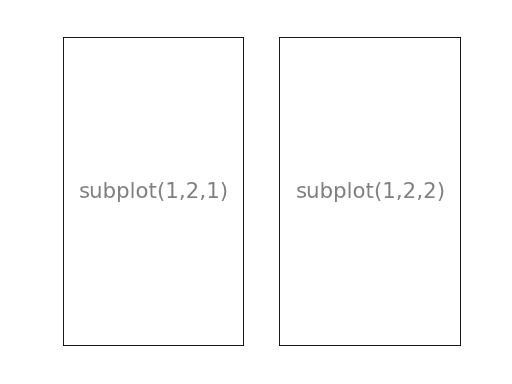
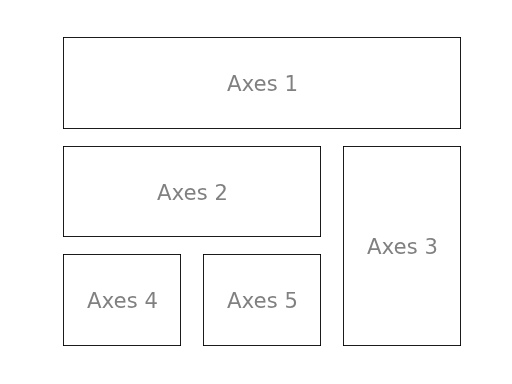
III-B. Vues en grille (matplotlib.subplot)▲

Les vues en grille (subplot) permettent d'organiser les différents tracés à l'intérieur d'une grille d'affichage. Il faut spécifier le nombre de lignes, le nombre de colonnes ainsi que le numéro du tracé. Notez toutefois que la commande gridspec() est une alternative beaucoup plus puissante.

subplot-horizontal.py

Cacher/Afficher le codeSélectionnez

from pylab import *

subplot(2,1,1)
xticks([]), yticks([])
text(0.5,0.5, 'subplot(2,1,1)',ha='center',va='center',size=24,alpha=.5)

subplot(2,1,2)
xticks([]), yticks([])
text(0.5,0.5, 'subplot(2,1,2)',ha='center',va='center',size=24,alpha=.5)

# plt.savefig('../figures/subplot-horizontal.png', dpi=64)
show()

subplot-vertical.py

Cacher/Afficher le codeSélectionnez

from pylab import *

subplot(1,2,1)
xticks([]), yticks([])
text(0.5,0.5, 'subplot(1,2,1)',ha='center',va='center',size=24,alpha=.5)

subplot(1,2,2)
xticks([]), yticks([])
text(0.5,0.5, 'subplot(1,2,2)',ha='center',va='center',size=24,alpha=.5)

# plt.savefig('../figures/subplot-vertical.png', dpi=64)
show()

subplot-grid.py

Cacher/Afficher le codeSélectionnez

from pylab import *

subplot(2,2,1)
xticks([]), yticks([])
text(0.5,0.5, 'subplot(2,2,1)',ha='center',va='center',size=20,alpha=.5)

subplot(2,2,2)
xticks([]), yticks([])
text(0.5,0.5, 'subplot(2,2,2)',ha='center',va='center',size=20,alpha=.5)

subplot(2,2,3)
xticks([]), yticks([])
text(0.5,0.5, 'subplot(2,2,3)',ha='center',va='center',size=20,alpha=.5)

subplot(2,2,4)
xticks([]), yticks([])
text(0.5,0.5, 'subplot(2,2,4)',ha='center',va='center',size=20,alpha=.5)

# savefig('../figures/subplot-grid.png', dpi=64)
show()

gridspec.py

Cacher/Afficher le codeSélectionnez

from pylab import *
import matplotlib.gridspec as gridspec

G = gridspec.GridSpec(3, 3)

axes_1 = subplot(G[0, :])
xticks([]), yticks([])
text(0.5,0.5, 'Axes 1',ha='center',va='center',size=24,alpha=.5)

axes_2 = subplot(G[1,:-1])
xticks([]), yticks([])
text(0.5,0.5, 'Axes 2',ha='center',va='center',size=24,alpha=.5)

axes_3 = subplot(G[1:, -1])
xticks([]), yticks([])
text(0.5,0.5, 'Axes 3',ha='center',va='center',size=24,alpha=.5)

axes_4 = subplot(G[-1,0])
xticks([]), yticks([])
text(0.5,0.5, 'Axes 4',ha='center',va='center',size=24,alpha=.5)

axes_5 = subplot(G[-1,-2])
xticks([]), yticks([])
text(0.5,0.5, 'Axes 5',ha='center',va='center',size=24,alpha=.5)

#plt.savefig('../figures/gridspec.png', dpi=64)
show()

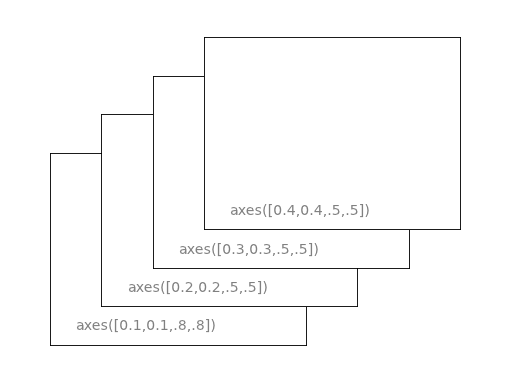
III-C. Vues libres (matplotlib.axes)▲

Les vues libres (axes) sont très similaires aux vues en grille (subplot) sauf qu'elles permettent un placement libre des tracés partout dans l'objet figure (la fenêtre GUI). Par exemple, pour placer un petit tracé dans un grand tracé, rien de plus simple avec les vues libres.

axes.py

Cacher/Afficher le codeSélectionnez

from pylab import *

axes([0.1,0.1,.8,.8])
xticks([]), yticks([])
text(0.6,0.6, 'axes([0.1,0.1,.8,.8])',ha='center',va='center',size=20,alpha=.5)

axes([0.2,0.2,.3,.3])
xticks([]), yticks([])
text(0.5,0.5, 'axes([0.2,0.2,.3,.3])',ha='center',va='center',size=16,alpha=.5)

plt.savefig("../figures/axes.png",dpi=64)
show()

axes-2.py

Cacher/Afficher le codeSélectionnez

from pylab import *

axes([0.1,0.1,.5,.5])
xticks([]), yticks([])
text(0.1,0.1, 'axes([0.1,0.1,.8,.8])',ha='left',va='center',size=16,alpha=.5)

axes([0.2,0.2,.5,.5])
xticks([]), yticks([])
text(0.1,0.1, 'axes([0.2,0.2,.5,.5])',ha='left',va='center',size=16,alpha=.5)

axes([0.3,0.3,.5,.5])
xticks([]), yticks([])
text(0.1,0.1, 'axes([0.3,0.3,.5,.5])',ha='left',va='center',size=16,alpha=.5)

axes([0.4,0.4,.5,.5])
xticks([]), yticks([])
text(0.1,0.1, 'axes([0.4,0.4,.5,.5])',ha='left',va='center',size=16,alpha=.5)

# plt.savefig("../figures/axes-2.png",dpi=64)
show()

III-D. Graduations de repère▲

Une présentation soignée des graduations de repère est une part importante du rendu final d'un graphique prêt à l'impression. Matplotlib fournit un système de graduations entièrement personnalisable. Les localisateurs (tick locators) permettent de préciser l'emplacement des graduations dans le tracé, alors que les formateurs (tick formatters) permettent une mise en forme des graduations selon vos exigences. Les graduations principales et secondaires peuvent être placées ou mises en forme indépendamment les unes des autres. Par défaut, les graduations secondaires ne sont pas affichées, elles correspondent en fait à une liste vide et un NullLocator (voir plus bas).

III-D-1. Localisateurs de graduations (tick locators)▲

Différentes classes de localisateurs en fonction des besoins :

Classe	Description
NullLocator	Aucune graduation.
IndexLocator	Affiche une graduation à chaque multiple d'un nombre fixe de points tracés.
FixedLocator	Les emplacements des graduations sont déterminés arbitrairement.
LinearLocator	Les emplacements des graduations sont déterminés linéairement à intervalles réguliers et à pas fixe.
MultipleLocator	Place une graduation à chaque entier multiple d'un nombre de base.
AutoLocator	Choisit au plus n intervalles et harmonise les emplacements.
LogLocator	Les emplacements des graduations sont déterminés pour les échelles logarithmiques.

Tous ces localisateurs dérivent de la classe ancêtre matplotlib.ticker.Locator. Vous pouvez créer votre propre localisateur en dérivant cette même classe ancêtre.

La gestion des dates comme graduations peut s'avérer particulièrement épineuse. Toutefois, matplotlib fournit quelques localisateurs spéciaux dans le module matplotlib.dates.

IV. Autres types de tracés▲

Tracés simplesTracés simples	Tracés en pointsTracés en points
HistogrammesHistogrammes	Tracés contourTracés contour
Image pixeliséeImage pixelisée	Tracés fléchésTracés fléchés
Graphiques en camembertGraphiques en camembert	GrillesGrilles
Tracés multiplesTracés multiples	Axes polairesAxes polaires
Graphiques en 3DGraphiques en 3D	TextesTextes

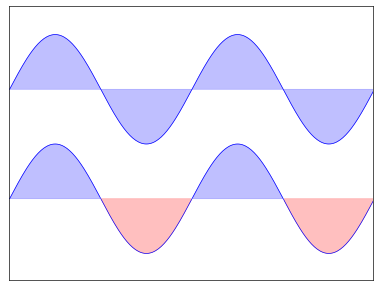
IV-A. Tracés simples▲

Indice

Vous aurez besoin de la commande fill_between().

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite (tenez compte des zones remplies) :

Sélectionnez

from pylab import *

n = 256
X = np.linspace(-np.pi,np.pi,n,endpoint=True)
Y = np.sin(2*X)

plot (X, Y+1, color='blue', alpha=1.00)
plot (X, Y-1, color='blue', alpha=1.00)
show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

plot_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

n = 256
X = np.linspace(-np.pi,np.pi,n,endpoint=True)
Y = np.sin(2*X)

axes([0.025,0.025,0.95,0.95])

plot (X, Y+1, color='blue', alpha=1.00)
fill_between(X, 1, Y+1, color='blue', alpha=.25)

plot (X, Y-1, color='blue', alpha=1.00)
fill_between(X, -1, Y-1, (Y-1) > -1, color='blue', alpha=.25)
fill_between(X, -1, Y-1, (Y-1) < -1, color='red',  alpha=.25)

xlim(-np.pi,np.pi), xticks([])
ylim(-2.5,2.5), yticks([])
# savefig('../figures/plot_ex.png',dpi=48)
show()

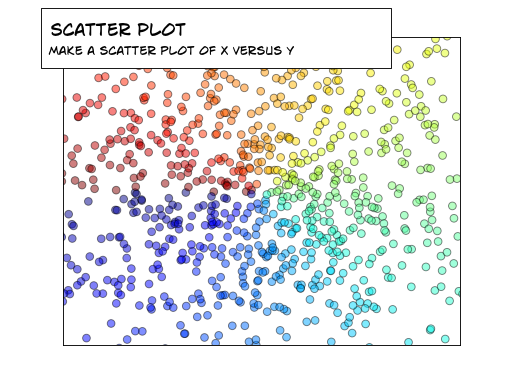
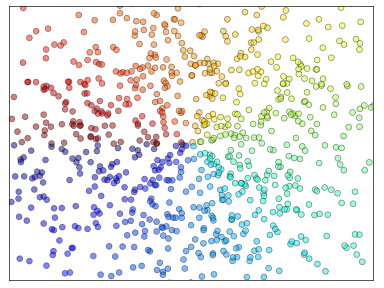
IV-B. Tracés en points▲

Indice

La couleur est calculée grâce à l'angle de (X,Y).

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite (tenez compte de la taille, de la couleur et de la transparence des points) :

Sélectionnez

from pylab import *

n = 1024
X = np.random.normal(0,1,n)
Y = np.random.normal(0,1,n)

scatter(X,Y)
show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

scatter_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

n = 1024
X = np.random.normal(0,1,n)
Y = np.random.normal(0,1,n)
T = np.arctan2(Y,X)

axes([0.025,0.025,0.95,0.95])
scatter(X,Y, s=75, c=T, alpha=.5)

xlim(-1.5,1.5), xticks([])
ylim(-1.5,1.5), yticks([])
# savefig('../figures/scatter_ex.png',dpi=48)
show()

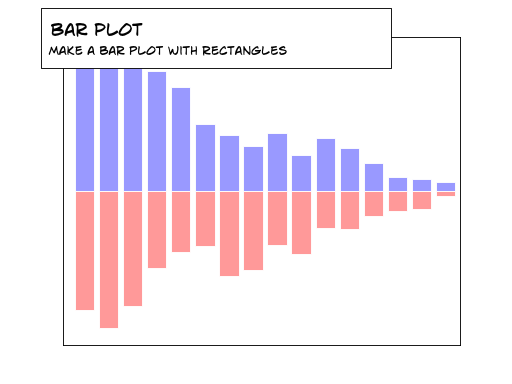
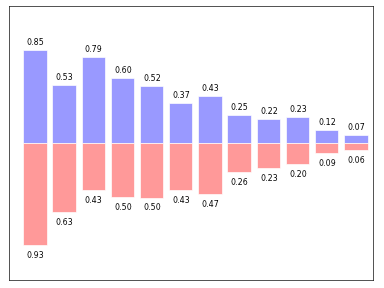
IV-C. Histogrammes▲

Indice

Vous devrez faire attention à l'alignement du texte.

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite (tenez compte qu'il faudra certainement ajouter des étiquettes texte aux barres rouges) :

Sélectionnez

from pylab import *

n = 12
X = np.arange(n)
Y1 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)
Y2 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)

bar(X, +Y1, facecolor='#9999ff', edgecolor='white')
bar(X, -Y2, facecolor='#ff9999', edgecolor='white')

for x,y in zip(X,Y1):
    text(x+0.4, y+0.05, '%.2f' % y, ha='center', va= 'bottom')

ylim(-1.25,+1.25)
show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

bar_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

n = 12
X = np.arange(n)
Y1 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)
Y2 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)

axes([0.025,0.025,0.95,0.95])
bar(X, +Y1, facecolor='#9999ff', edgecolor='white')
bar(X, -Y2, facecolor='#ff9999', edgecolor='white')

for x,y in zip(X,Y1):
    text(x+0.4, y+0.05, '%.2f' % y, ha='center', va= 'bottom')

for x,y in zip(X,Y2):
    text(x+0.4, -y-0.05, '%.2f' % y, ha='center', va= 'top')

xlim(-.5,n), xticks([])
ylim(-1.25,+1.25), yticks([])

# savefig('../figures/bar_ex.png', dpi=48)
show()

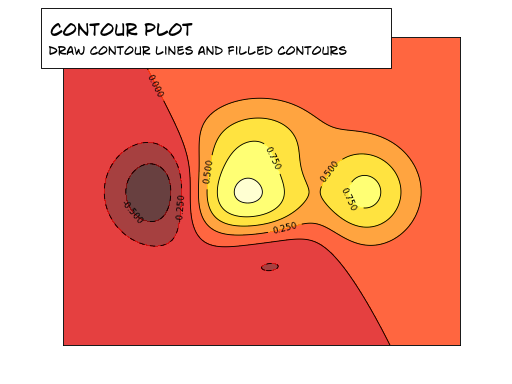
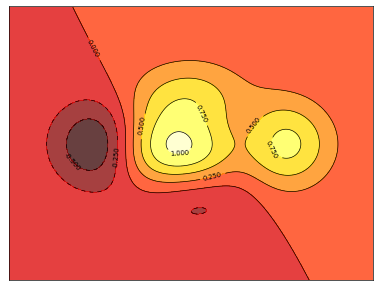
IV-D. Tracés contour▲

Indice

Vous aurez besoin de la commande clabel().

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite (tenez compte des bandes colorées - voir RéférenceBandes coloréesplus bas) :

Sélectionnez

from pylab import *

def f(x,y): return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)

n = 256
x = np.linspace(-3,3,n)
y = np.linspace(-3,3,n)
X,Y = np.meshgrid(x,y)

contourf(X, Y, f(X,Y), 8, alpha=.75, cmap='jet')
C = contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5)
show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

contour_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

def f(x,y): return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)

n = 256
x = np.linspace(-3,3,n)
y = np.linspace(-3,3,n)
X,Y = np.meshgrid(x,y)

axes([0.025,0.025,0.95,0.95])

contourf(X, Y, f(X,Y), 8, alpha=.75, cmap=cm.hot)
C = contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5)
clabel(C, inline=1, fontsize=10)

xticks([]), yticks([])
# savefig('../figures/contour_ex.png',dpi=48)
show()

IV-E. Image pixelisée▲

Indice

Vous devrez faire attention au point d'origine de l'image dans la commande imshow() et utiliser une barre colorée (colorbar).

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite (tenez compte de la bande colorée, de l'interpolation de l'image et du point d'origine) :

Sélectionnez

from pylab import *

def f(x,y): return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)

n = 10
x = np.linspace(-3,3,4*n)
y = np.linspace(-3,3,3*n)
X,Y = np.meshgrid(x,y)
imshow(f(X,Y)), show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

imshow_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

def f(x,y): return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)

n = 10
x = np.linspace(-3,3,3.5*n)
y = np.linspace(-3,3,3.0*n)
X,Y = np.meshgrid(x,y)
Z = f(X,Y)

axes([0.025,0.025,0.95,0.95])
imshow(Z,interpolation='nearest', cmap='bone', origin='lower')
colorbar(shrink=.92)

xticks([]), yticks([])
# savefig('../figures/imshow_ex.png', dpi=48)
show()

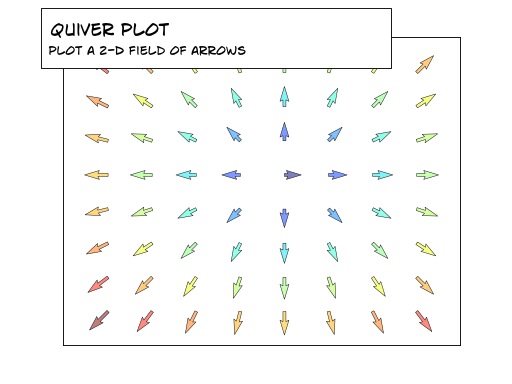
IV-F. Tracés fléchés▲

Indice

Vous devrez dessiner les flèches deux fois.

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite (tenez compte des couleurs et des orientations des flèches) :

Sélectionnez

from pylab import *

n = 8
X,Y = np.mgrid[0:n,0:n]
quiver(X,Y), show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

quiver_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

n = 8
X,Y = np.mgrid[0:n,0:n]
T = np.arctan2(Y-n/2.0, X-n/2.0)
R = 10+np.sqrt((Y-n/2.0)**2+(X-n/2.0)**2)
U,V = R*np.cos(T), R*np.sin(T)

axes([0.025,0.025,0.95,0.95])
quiver(X,Y,U,V,R, alpha=.5)
quiver(X,Y,U,V, edgecolor='k', facecolor='None', linewidth=.5)

xlim(-1,n), xticks([])
ylim(-1,n), yticks([])

# savefig('../figures/quiver_ex.png',dpi=48)
show()

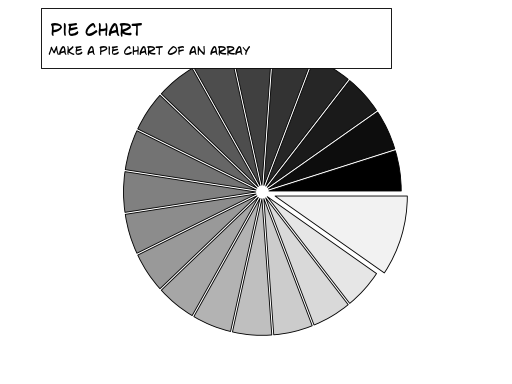
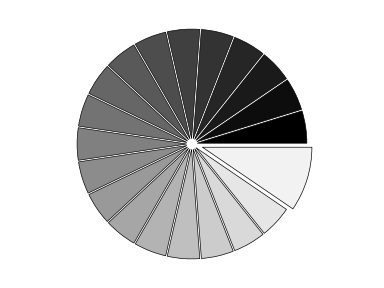
IV-G. Graphiques en camembert▲

Indice

Vous devrez modifier Z.

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite (tenez compte des couleurs et de la taille des portions) :

Sélectionnez

from pylab import *

n = 20
Z = np.random.uniform(0,1,n)
pie(Z), show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

pie_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

n = 20
Z = np.ones(n)
Z[-1] *= 2

axes([0.025,0.025,0.95,0.95])

pie(Z, explode=Z*.05, colors = ['%f' % (i/float(n)) for i in range(n)])
gca().set_aspect('equal')
xticks([]), plt.yticks([])

# savefig('../figures/pie_ex.png',dpi=48)
show()

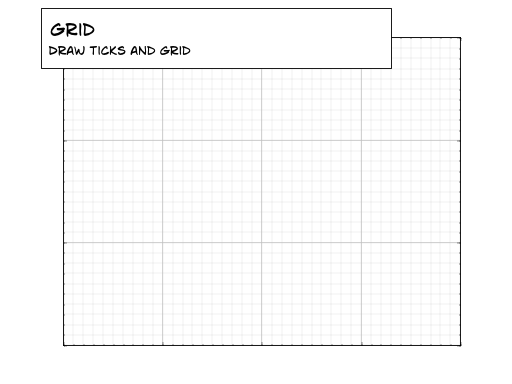
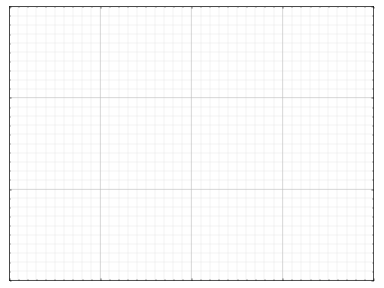
IV-H. Grilles▲

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite (tenez compte des styles de trait) :

Sélectionnez

from pylab import *

axes = gca()
axes.set_xlim(0,4)
axes.set_ylim(0,3)
axes.set_xticklabels([])
axes.set_yticklabels([])

show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

grid_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

ax = axes([0.025,0.025,0.95,0.95])

ax.set_xlim(0,4)
ax.set_ylim(0,3)
ax.xaxis.set_major_locator(MultipleLocator(1.0))
ax.xaxis.set_minor_locator(MultipleLocator(0.1))
ax.yaxis.set_major_locator(MultipleLocator(1.0))
ax.yaxis.set_minor_locator(MultipleLocator(0.1))
ax.grid(which='major', axis='x', linewidth=0.75, linestyle='-', color='0.75')
ax.grid(which='minor', axis='x', linewidth=0.25, linestyle='-', color='0.75')
ax.grid(which='major', axis='y', linewidth=0.75, linestyle='-', color='0.75')
ax.grid(which='minor', axis='y', linewidth=0.25, linestyle='-', color='0.75')
ax.set_xticklabels([])
ax.set_yticklabels([])

# savefig('../figures/grid_ex.png',dpi=48)
show()

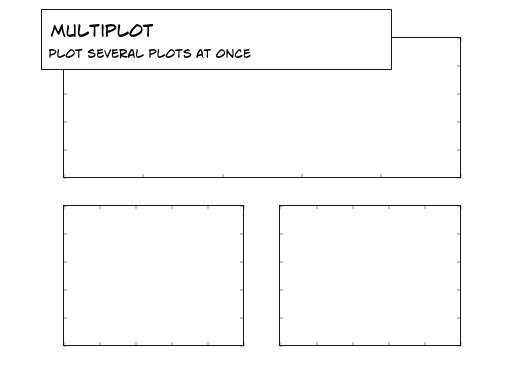
IV-I. Tracés multiples▲

Indice

Vous pouvez utiliser plusieurs vues avec différents découpages.

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite :

Sélectionnez

from pylab import *

subplot(2,2,1)
subplot(2,2,3)
subplot(2,2,4)

show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

multiplot_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

fig =figure()
fig.subplots_adjust(bottom=0.025, left=0.025, top = 0.975, right=0.975)

subplot(2,1,1)
xticks([]), yticks([])

subplot(2,3,4)
xticks([]), yticks([])

subplot(2,3,5)
xticks([]), yticks([])

subplot(2,3,6)
xticks([]), yticks([])

savefig('../figures/multiplot_ex.png',dpi=48)
show()

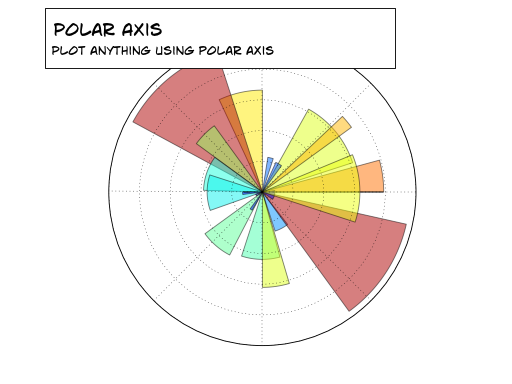
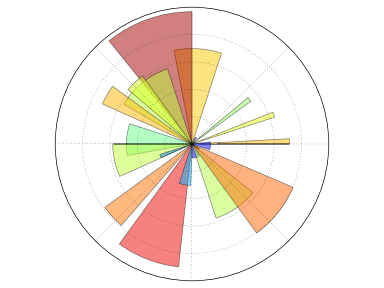
IV-J. Axes polaires▲

Indice

Vous aurez uniquement besoin de modifier le tracé des axes.

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite :

Sélectionnez

from pylab import *

axes([0,0,1,1])

N = 20
theta = np.arange(0.0, 2*np.pi, 2*np.pi/N)
radii = 10*np.random.rand(N)
width = np.pi/4*np.random.rand(N)
bars = bar(theta, radii, width=width, bottom=0.0)

for r,bar in zip(radii, bars):
    bar.set_facecolor( cm.jet(r/10.))
    bar.set_alpha(0.5)

show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

polar_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

ax = axes([0.025,0.025,0.95,0.95], polar=True)

N = 20
theta = np.arange(0.0, 2*np.pi, 2*np.pi/N)
radii = 10*np.random.rand(N)
width = np.pi/4*np.random.rand(N)
bars = bar(theta, radii, width=width, bottom=0.0)

for r,bar in zip(radii, bars):
    bar.set_facecolor( cm.jet(r/10.))
    bar.set_alpha(0.5)

ax.set_xticklabels([])
ax.set_yticklabels([])
# savefig('../figures/polar_ex.png',dpi=48)
show()

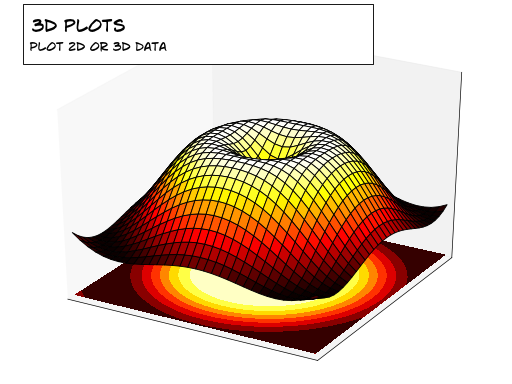
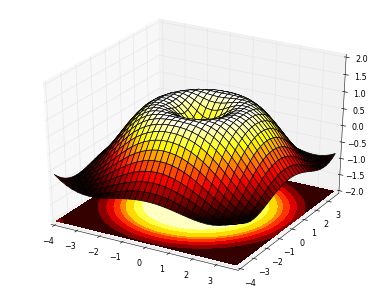
IV-K. Graphiques en 3D▲

Indice

Vous aurez besoin de la commande contourf().

En vous basant sur le code suivant, essayez d'obtenir le graphique représenté dans l'illustration de droite :

Sélectionnez

from pylab import *
from mpl_toolkits.mplot3d import Axes3D

fig = figure()
ax = Axes3D(fig)
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='hot')

show()

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

plot3d_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *
from mpl_toolkits.mplot3d import Axes3D

fig = figure()
ax = Axes3D(fig)
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.hot)
ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap=cm.hot)
ax.set_zlim(-2,2)

# savefig('../figures/plot3d_ex.png',dpi=48)
show()

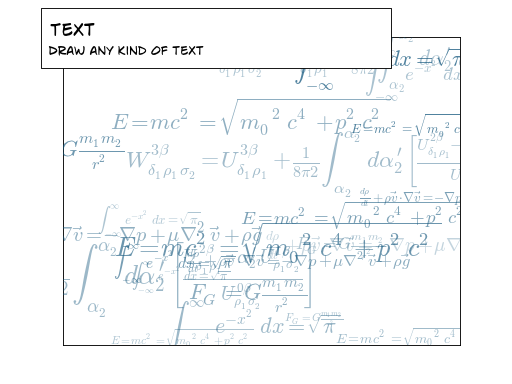
IV-L. Textes▲

Indice

Jetez un œil au logo matplotlib.

Essayez de faire pareil à partir de zéro !

Image non disponible

Cliquez sur Image non disponible pour voir la réponse.

text_ex.py

Cacher/Afficher le codeSélectionnez

from pylab import *

eqs = []
eqs.append((r"$W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2} \int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 \left[\frac{ U^{2\beta}_{\delta_1 \rho_1} - \alpha^\prime_2U^{1\beta}_{\rho_1 \sigma_2} }{U^{0\beta}_{\rho_1 \sigma_2}}\right]$"))
eqs.append((r"$\frac{d\rho}{d t} + \rho \vec{v}\cdot\nabla\vec{v} = -\nabla p + \mu\nabla^2 \vec{v} + \rho \vec{g}$"))
eqs.append((r"$\int_{-\infty}^\infty e^{-x^2}dx=\sqrt{\pi}$"))
eqs.append((r"$E = mc^2 = \sqrt{{m_0}^2c^4 + p^2c^2}$"))
eqs.append((r"$F_G = G\frac{m_1m_2}{r^2}$"))


axes([0.025,0.025,0.95,0.95])

for i in range(24):
    index = np.random.randint(0,len(eqs))
    eq = eqs[index]
    size = np.random.uniform(12,32)
    x,y = np.random.uniform(0,1,2)
    alpha = np.random.uniform(0.25,.75)
    text(x, y, eq, ha='center', va='center', color="#11557c", alpha=alpha,
         transform=gca().transAxes, fontsize=size, clip_on=True)
xticks([]), yticks([])
# savefig('../figures/text_ex.png',dpi=48)
show()

V. Aller plus loin▲

Matplotlib bénéficie d'une documentation riche et variée, de même que d'une vaste communauté d'utilisateurs et de développeurs. Ci-dessous, quelques liens dignes d'intérêt.

V-A. Tutoriels▲

Tutoriel pyplot
- Présentation
- Gérer les propriétés de trait
- Travailler avec plusieurs objets figure et plusieurs vues
- Travailler avec du texte
Tutoriel image
- Commandes de départ
- Importer des données image dans des tableaux numpy
- Représenter des tableaux numpy comme des images
Tutoriel texte
- Présentation
- Commandes de texte élémentaires
- Propriétés de textes et modes d'affichage
- Écrire des formules mathématiques
- Rendu de texte avec LaTeX
- Annoter du texte
Tutoriel pour artistes
- Présentation
- Personnaliser vos objets
- Conteneurs d'objets
- Conteneur graphique (matplotlib.figure)
- Conteneur de vues libres (matplotlib.axes)
- Conteneurs d'axes de repère
- Conteneurs de graduations
Tutoriels chemins
- Présentation
- Exemple de courbe de Bézier
- Chemins mélangés
Tutoriel transformations
- Présentation
- Coordonnées 'data'
- Coordonnées de vues libres (matplotlib.axes)
- Transformations de dégradés (gradients)
- Utiliser les transformations offset pour créer un effet d'ombre projetée
- Le mécanisme de transformation(pipeline)

V-B. Documentation Matplotlib▲

Guide utilisateur
FAQ - Foire Aux Questions
- Installation de matplotlib
- Utilisation
- Recettes de cuisine (How-To)
- Problèmes et solutions
- Variables d'environnement
Captures d'écran

V-C. Documentation du code▲

Le code source de matplotlib est particulièrement bien documenté ; vous pouvez même obtenir une aide rapide sur telle ou telle commande directement dans une console Python :

Sélectionnez

>>> from pylab import *
>>> help(plot)
Help on function plot in module matplotlib.pyplot:

plot(*args, **kwargs)
   Plot lines and/or markers to the
   :class:`~matplotlib.axes.Axes`.  *args* is a variable length
   argument, allowing for multiple *x*, *y* pairs with an
   optional format string.  For example, each of the following is
   legal::

       plot(x, y)         # plot x and y using default line style and color
       plot(x, y, 'bo')   # plot x and y using blue circle markers
       plot(y)            # plot y using x as index array 0..N-1
       plot(y, 'r+')      # ditto, but with red plusses

   If *x* and/or *y* is 2-dimensional, then the corresponding columns
   will be plotted.
   ...

V-D. Galeries▲

La galerie matplotlib est incroyablement utile lorsque l'on cherche un exemple pour un type de graphique en particulier. Chaque exemple est accompagné de son code source.

Il existe une autre galerie plus modeste à cet endroit.

V-E. Mailing lists▲

Pour finir, vous disposez d'une mailing list utilisateurs où vous pourrez demander de l'aide et une mailing list développeurs pour les questions plus techniques.

VI. Références▲

Ci-dessous quelques tableaux illustrant les principaux styles et propriétés de trait.

VI-A. Propriétés de trait▲

Propriété	Description	Apparence
alpha (ou a)	Transparence alpha (ratio compris entre 0 et 1)
antialiased	Rendu anti-crénelage (booléen)
color (ou c)	Couleur matplotlib
linestyle (ou ls)	cf. Styles de traitStyles de trait
linewidth (ou lw)	Épaisseur du trait en points (float)
solid_capstyle	Style de fin de trait pour traits pleins
solid_joinstyle	Style de jointure pour traits pleins
dash_capstyle	Style de fin de trait pour pointillés
dash_joinstyle	Style de jointure pour pointillés
marker	cf. MarquesMarques
markeredgewidth (mew)	Épaisseur du contour d'une marque
markeredgecolor (mec)	Couleur du contour d'une marque
markerfacecolor (mfc)	Couleur d'une marque
markersize (ms)	Taille de la marque en points

VI-B. Styles de trait▲

Symbole	Description	Apparence
-	Trait plein
--	Pointillé long
-.	Pointillé mixte
:	Pointillé court
.	Gros points
,	Pixels
o	Cercles
^	Triangles vers le haut
v	Triangles vers le bas
<	Triangles vers la gauche
>	Triangles vers la droite
s	Carrés
+	Signes 'plus' (+)
x	Signes 'croix' (x)
D	Diamants carrés (<>)
d	Losanges
1	Tripodes vers le bas
2	Tripodes vers le haut
3	Tripodes vers la gauche
4	Tripodes vers la droite
h	Hexagones verticaux
H	Hexagones horizontaux
p	Pentagones
\|	Traits verticaux
_	Traits horizontaux

VI-C. Marques▲

Symbole	Description	Apparence
0	Graduation à gauche
1	Graduation à droite
2	Graduation en haut
3	Graduation en bas
4	Lambda à gauche
5	Lambda à droite
6	Lambda en haut
7	Lambda en bas
o	Cercles
D	Diamants carrés (<>)
h	Hexagones verticaux
H	Hexagones horizontaux
_	Traits horizontaux
1	Tripodes vers le bas
2	Tripodes vers le haut
3	Tripodes vers la gauche
4	Tripodes vers la droite
8	Octogones
p	Pentagones
^	Triangles vers le haut
v	Triangles vers le bas
<	Triangles vers la gauche
>	Triangles vers la droite
d	Losanges
,	Pixels
+	Signes 'plus' (+)
.	Gros points
s	Carrés
*	Étoiles à cinq branches
\|	Traits verticaux
x	Signes 'croix' (x)
r'$\sqrt{2}$'	Toute expression LaTeX

VI-D. Bandes colorées▲

Toutes les bandes colorées peuvent être inversées en ajoutant _r en fin de nom. Par exemple, gray_r sera l'inverse de gray.

Veuillez consulter documenter les bandes colorées matplotlib pour plus d'information.

VI-D-1. De base▲

Nom	Apparence
autumn
bone
cool
copper
flag
gray
hot
hsv
jet
pink
prism
spectral
spring
summer
winter

VI-D-2. GIST▲

Nom	Apparence
gist_earth
gist_gray
gist_heat
gist_ncar
gist_rainbow
gist_stern
gist_yarg

VI-D-3. Séquences▲

Nom	Apparence
BrBG
PiYG
PRGn
PuOr
RdBu
RdGy
RdYlBu
RdYlGn
Spectral

VI-D-4. Dégradés▲

Nom	Apparence
Blues
BuGn
BuPu
GnBu
Greens
Greys
Oranges
OrRd
PuBu
PuBuGn
PuRd
Purples
RdPu
Reds
YlGn
YlGnBu
YlOrBr
YlOrRd

VI-D-5. Qualifiés▲

Nom	Apparence
Accent
Dark2
Paired
Pastel1
Pastel2
Set1
Set2
Set3

VI-D-6. Divers▲

Nom	Apparence
afmhot
binary
brg
bwr
coolwarm
CMRmap
cubehelix
gnuplot
gnuplot2
ocean
rainbow
seismic
terrain

VII. Notes et remerciements de l'auteur▲

Le présent document est basé sur le tutoriel de Mike Müller disponible sur le site scipy lectures.

Les textes originaux sont disponibles ici. Les illustrations se trouvent dans ce répertoire et les scripts dans celui-ci. Le répertoire Github est ici.

Les codes sources et les ressources sont publiés sous licence Creative Commons Paternité 3.0 - licence USA (CC-by) http://creativecommons.org/licenses/by/3.0/us.

Un grand merci à Bill Wing, Christoph Deil et Wojciech Mamrak pour la relecture et les corrections.

Des illustrations de présentation de diverses techniques de représentation graphique scientifique se trouvent à cet endroit.

Il existe désormais un tutoriel numpy d'accompagnement.

VIII. Remerciements Developpez▲

Nous remercions Nicolas Rougier qui nous a aimablement autorisés à traduire son article Matlab Tutorial.

Nos remerciements à Raphaël SEBAN (tarball69) pour la traduction et à Fabien (f-leb) pour la mise au gabarit.

Merci également à Malick Seck (milkoseck) pour sa relecture orthographique.

Vous avez aimé ce tutoriel ? Alors partagez-le en cliquant sur les boutons suivants :

En complément sur Developpez.com

Condensé Python pour les scientifiques - Partie 1