6. Modules et packages▲

Un programme Python est généralement composé de plusieurs fichiers source, appelés modules.
S'ils sont correctement codés les modules doivent être indépendants les uns des autres pour être réutilisés à la demande dans d'autres programmes.
Ce chapitre explique comment coder des modules et comment les importer dans un autre.
Nous verrons également la notion de package qui permet de grouper plusieurs modules.
6-1. Modules▲
Module : fichier script Python permettant de définir des éléments de programme réutilisables. Ce mécanisme permet d'élaborer efficacement des bibliothèques de fonctions ou de classes.
Avantages des modules :
- réutilisation du code ;
- la documentation et les tests peuvent être intégrés au module ;
- réalisation de services ou de données partagés ;
- partition de l'espace de noms du système.
Lorsqu'on parle du module, on omet l'extension : le module machin est dans le fichier machin.py.
6-1-1. Import▲
L'instruction import charge et exécute le module indiqué s'il n'est pas déjà chargé. L'ensemble des définitions contenues dans ce module deviennent alors disponibles : variables globales, fonctions, classes.
Suivant la syntaxe utilisée, on accède aux définitions du module de différentes façons :
-
l'instruction
import<nom_module>donne accès à l'ensemble des définitions du module importé en utilisant le nom du module comme espace de nom.Sélectionnez>>>importtkinter>>>print("Version de tkinter :", tkinter.TkVersion) Version de tkinter :8.5 - l'instruction
from<nom_module>importnom1, nom2… donne accès directement à une sélection choisie de noms définis dans le module.
>>> from math import pi, sin
>>> print("Valeur de Pi :", pi, "sinus(pi/4) :", sin(pi/4))
Valeur de Pi : 3.14159265359 sinus(pi/4) : 0.707106781187Dans les deux cas, le module et ses définitions existent dans leur espace mémoire propre, et on duplique simplement dans le module courant les noms que l'on a choisis, comme si on avait fait les affectations :
>>> sin = math.sin
>>> pi = math.piIl est conseillé d'importer dans l'ordre :
- les modules de la bibliothèque standard ;
- les modules des bibliothèques tierces ;
- les modules personnels.
Pour tout ce qui est fonction et classe, ainsi que pour les « constantes » (variables globales définies et affectées une fois pour toutes à une valeur), l'import direct du nom ne pose pas de problème.
Par contre, pour les variables globales que l'on désire pouvoir modifier, il est préconisé de passer systématiquement par l'espace de nom du module afin de s'assurer de l'existence de cette variable en un unique exemplaire ayant la même valeur dans tout le programme.
6-1-2. Exemples▲
6-1-2-a. Notion d'« autotest »▲
Le module principal est celui qui est donné en argument sur la ligne de commande ou qui est lancé en premier lors de l'exécution d'un script. Son nom est contenu dans la variable globale __name__. Sa valeur dépend du contexte de l'exécution.
Soit le module :
# je_me_nomme.py
print("Je me nomme :", __name__)Premier contexte exécution sur la ligne de commande (ou dans un EDI), on obtient la valeur de la variable prédéfinie __main__ :
$ python3 je_me_nomme.py
Je me nomme : __main__Second contexte import de ce module (ce n'est donc plus le module principal), on obtient l'identificateur du module :
>>> import je_me_nomme
Je me nomme : je_me_nommeGrâce à un test, on peut donc facilement savoir si le code est exécuté en tant que script principal :
- on écrit un script de fonctions ou de classes (souvent appelé bibliothèque) et on termine le fichier par un test, l'« autotest », pour vérifier que l'on est dans le module principal. On en profite pour vérifier tous les éléments de la bibliothèque ;
- quand on importe le script, le test inclus est faux et on se borne à utiliser la bibliothèque.
def cube(x) :
"""retourne le cube de <x>."""
return x**3
# autotest ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
if __name__ == "__main__" : # vrai car module principal
if cube(9) == 729:
print("OK !")
else :
print("KO !")Utilisation de ce module dans un autre (par exemple celui qui contient le programme principal) :
import cube
# programme principal ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
for i in range(1, 4) :
print("cube de", i, "=", cube_m.cube(i))
"""
cube de 1 = 1
cube de 2 = 8
cube de 3 = 27
"""Autre exemple :
def ok(message) :
"""
Retourne True si on saisit <Entrée>, <O>, <o>, <Y> ou <y>,
False dans tous les autres cas.
"""
s = input(message + " (O/n) ?")
return True if s == "" or s[0] in "OoYy" else False
# autotest ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
if __name__ == '__main__' :
while True :
if ok("Encore") :
print("Je continue")
else :
print("Je m'arrête")
break
"""
Encore (O/n) ?
Je continue
Encore (O/n) ? o
Je continue
Encore (O/n) ? n
Je m'arrête
"""6-2. Batteries included▲
On dit souvent que Python est livré « piles comprises » (batteries included) tant sa bibliothèque standard, riche de plus de 200 packages et modules, répond aux problèmes courants les plus variés.
Ce survol présente quelques fonctionnalités utiles.
6-2-1. La gestion des chaînes▲
Le module string fournit des constantes comme ascii_lowercase, digits… ainsi que la classe Formatter qui peut être spécialisée en sous-classes de formateurs de chaînes.
Le module textwrap est utilisé pour formater un texte : longueur de chaque ligne, contrôle de l'indentation.
Le module struct permet de convertir des nombres, booléens et des chaînes en leur représentation binaire afin de communiquer avec des bibliothèques de bas-niveau (souvent en C).
Le module difflib permet la comparaison de séquences et fournit des sorties au format standard diff ou en HTML.
Enfin, on ne saurait oublier le module re qui offre à Python la puissance des expressions régulières(16).
6-2-2. La gestion de la ligne de commande▲
Pour gérer la ligne de commande, Python propose l'instruction sys.argv. Elle fournit simplement une liste contenant les arguments de la ligne de commande : argv[1], argv[2]… sachant que argv[0] est le nom du script lui-même.
Par ailleurs, Python propose un module de parsing(17), le module argparse.
C'est un module objet qui s'utilise en trois étapes :
- Création d'un objet parser ;
- Ajout des arguments prévus en utilisant la méthode add_argument(). Chaque argument peut déclencher une action particulière spécifiée dans la méthode ;
- Analyse de la ligne de commande par la méthode parse_args().
Enfin, selon les paramètres détectés par l'analyse, on effectue les actions adaptées.
Dans l'exemple suivant, extrait de la documentation officielle du module, on se propose de donner en argument à la ligne de commande une liste d'entiers. Par défaut le programme retourne le plus grand entier de la liste, mais s'il détecte l'argument -sum, il retourne la somme des entiers de la liste. De plus, lancé avec l'option -h ou -help, le module argparse fournit automatiquement une documentation du programme :
# -*- coding : utf8 -*-
import argparse
# 1. création du parser
parser = argparse.ArgumentParser(description='Process some integers')
# 2. ajout des arguments
parser.add_argument('integers', metavar='N', type=int, nargs='+',
help='an integer for the accumulator')
parser.add_argument('--sum', dest='accumulate', action='store_const',
const=sum, default=max,
help='sum the integers (default : find the max')
# 3. parsing de la ligne de commande
args = parser.parse_args()
# processing
print(args.accumulate(args.integers))Voici les sorties correspondant aux différents cas de la ligne de commande :
$ python argparse.py -h
usage: argparse.py [-h] [--sum] N [N ...]
Process some integers.
positional arguments:
N an integer for the accumulator
optional arguments:
-h, --help show this help message and exit
--sum sum the integers (default: find the max)
$ python argparse.py --help
usage: argparse.py [-h] [--sum] N [N ...]
Process some integers.
positional arguments:
N an integer for the accumulator
optional arguments:
-h, --help show this help message and exit
--sum sum the integers (default: find the max)
$ python argparse.py 1 2 3 4 5 6 7 8 9
9
$ python argparse.py 1 2 3 4 5 6 7 8 9 --sum
456-2-3. La gestion du temps et des dates▲
Les modules calendar, time et datetime fournissent les fonctions courantes de gestion du temps et des durées :
import calendar, datetime, time
moon_apollo11 = datetime.datetime(1969, 7, 20, 20, 17, 40)
print(moon_apollo11)
print(time.asctime(time.gmtime(0)))
# Thu Jan 01 00:00:00 1970 ("epoch" UNIX)
vendredi_precedent = datetime.date.today()
un_jour = datetime.timedelta(days=1)
while vendredi_precedent.weekday() != calendar.FRIDAY :
vendredi_precedent -= un_jour
print(vendredi_precedent.strftime("%A, %d-%b-%Y"))
# Friday, 09-Oct-20096-2-4. Algorithmes et types de données collection▲
Le module bisect fournit des fonctions de recherche de séquences triées. Le module array propose un type semblable à la liste, mais plus rapide, car de contenu homogène.
Le module heapq gère des tas dans lesquels l'élément d'index 0 est toujours le plus petit :
import heapq
import random
heap = []
for i in range(10) :
heapq.heappush(heap, random.randint(2, 9))
print(heap) # [2, 3, 5, 4, 6, 6, 7, 8, 7, 8]À l'instar des structures C, Python propose désormais, via le module collections, la notion de type tuple nommé (il est bien sûr possible d'avoir des tuples nommés emboîtés) :
import collections
# description du type :
Point = collections.namedtuple("Point", "x y z")
# on instancie un point :
point = Point(1.2, 2.3, 3.4)
# on l'affiche :
print("point : [{}, {}, {}]"
.format(point.x, point.y, point.z)) # point : [1.2, 2.3, 3.4]Le type defaultdict permet des utilisations avancées :
from collections import defaultdict
s = [('y', 1), ('b', 2), ('y', 3), ('b', 4), ('r', 1)]
d = defaultdict(list)
for k, v in s :
d[k].append(v)
print(d.items())
# dict_items([('y', [1, 3]), ('r', [1]), ('b', [2, 4])])
s = 'mississippi'
d = defaultdict(int)
for k in s :
d[k] += 1
print(d.items())
# dict_items([('i', 4), ('p', 2), ('s', 4), ('m', 1)])6-2-5. Et tant d'autres domaines…▲
Beaucoup d'autres sujets pourraient être explorés :
- accès au système ;
- utilitaires fichiers ;
- programmation réseau ;
- persistance ;
- les fichiers XML ;
- la compression ;
- …
6-3. Python scientifique▲
Dans les années 1990, Travis Oliphant et d'autres commencèrent à élaborer des outils efficaces de traitement des données numériques : Numeric, Numarray, et enfin NumPy. SciPy, bibliothèque d'algorithmes scientifiques, a également été créée à partir de NumPy. Au début des années 2000, John Hunter crée matplotlib un module de tracer de graphiques 2D. À la même époque Fernando Perez crée IPython en vue d'améliorer l'interactivité et la productivité en Python.
En moins de 10 ans après sa création, les outils essentiels pour faire de Python un langage scientifique performant étaient en place.
6-3-1. Bibliothèques mathématiques et types numériques▲
On rappelle que Python possède la bibliothèque math :
>>> import math
>>> math.pi / math.e
1.1557273497909217
>>> math.exp(1e-5) - 1
1.0000050000069649e-05
>>> math.log(10)
2.302585092994046
>>> math.log(1024, 2)
10.0
>>> math.cos(math.pi/4)
0.7071067811865476
>>> math.atan(4.1/9.02)
0.4266274931268761
>>> math.hypot(3, 4)
5.0
>>> math.degrees(1)
57.29577951308232Par ailleurs, Python propose en standard les modules fraction et decimal :
from fractions import Fraction
import decimal as d
print(Fraction(16, -10)) # -8/5
print(Fraction(123)) # 123
print(Fraction(' -3/7 ')) # -3/7
print(Fraction('-.125')) # -1/8
print(Fraction('7e-6')) # 7/1000000
d.getcontext().prec = 6
print(d.Decimal(1) / d.Decimal(7)) # 0.142857
d.getcontext().prec = 18
print(d.Decimal(1) / d.Decimal(7)) # 0.142857142857142857En plus des bibliothèques math et cmath déjà vues, la bibliothèque random propose plusieurs fonctions de nombres aléatoires.
6-3-2. L'interpréteur IPython▲
On peut dire que IPython est devenu de facto l'interpréteur standard du Python scientifique.
En mars 2013, ce projet a valu le Prix du développement logiciel libre par la Free Software Foundation à son créateur Fernando Perez. Depuis début 2013 et pour deux ans, la fondation Alfred P. Sloan subventionne le développement de IPython.
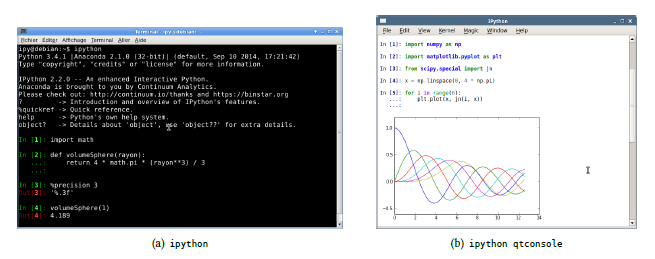
IPython (actuellement en version 2.X) est disponible en trois déclinaisons (Fig. 6.1 et 6.2) :
- ipython : l'interpréteur de base ;
- ipython qtconsole : sa version améliorée dans une fenêtre graphique de la bibliothèque graphique Qt, agrémentée d'un menu ;
- ipython notebook : sa dernière variante qui offre une interface simple, mais très puissante dans le navigateur par défaut.
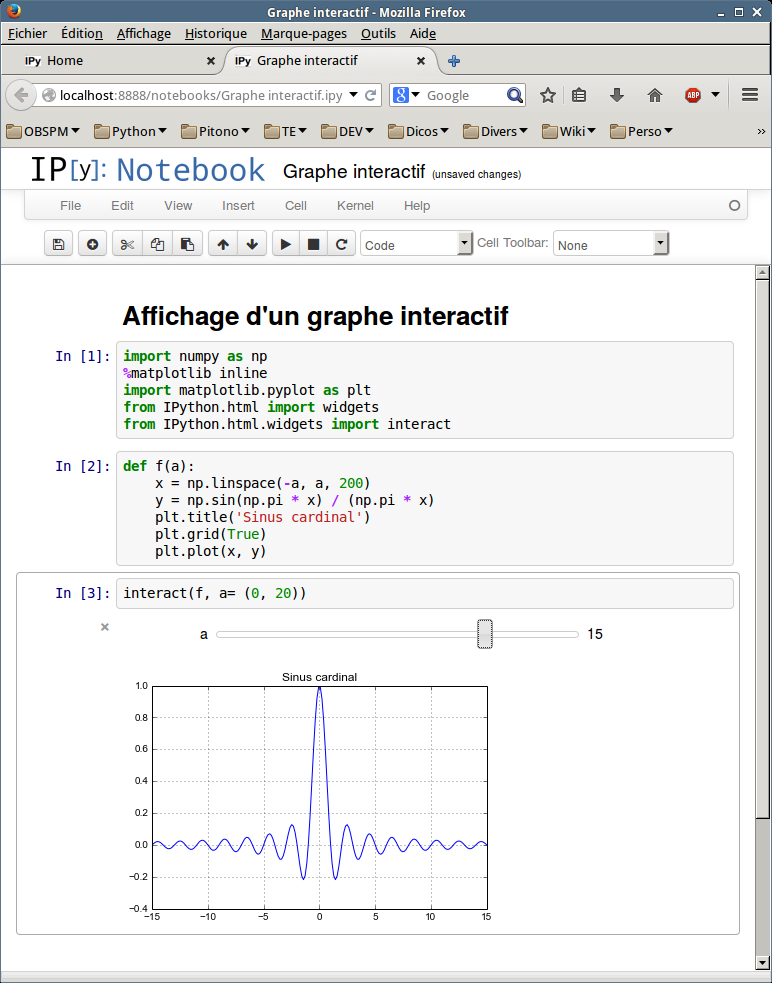
La version notebook mérite une mention spéciale : chaque cellule du notebook peut être du code, des figures, du texte enrichi (y compris des formules mathématiques), des vidéos, etc.
La figure 6.2 présente un exemple de tracé interactif.
6-3-2-a. Objectifs▲
D'après ses concepteurs, les objectifs d'IPython sont les suivants :
- fournir un interpréteur Python plus puissant que celui par défaut. IPython propose de nombreuses caractéristiques comme l'introspection d'objet, l'accès au shell système ainsi que ses propres commandes permettant une grande interaction avec l'utilisateur ;
- proposer un interpréteur embarquable et prêt à l'emploi pour vos programmes Python. IPython s'efforce d'être un environnement efficace à la fois pour le développement de code Python et pour la résolution des problèmes liés à l'utilisation d'objets Python ;
- offrir un ensemble de bibliothèques pouvant être utilisé comme environnement pour d'autres systèmes utilisant Python comme langage sous-jacent (particulièrement pour les environnements scientifiques comme MATLAB, Maple ou Mathematica) ;
- permettre le test interactif des bibliothèques graphiques gérées comme Tkinter, wxPython, PyGTK alors que IDLE ne le permet qu'avec des applications Tkinter.
6-3-2-b. Quelques caractéristiques▲
- IPython est autodocumenté.
- Coloration syntaxique.
- Les docstrings des objets Python sont disponibles en accolant un « ? » au nom de l'objet ou « ?? » pour une aide plus détaillée.
- Numérote les entrées et les sorties.
- Organise les sorties : messages d'erreur ou retour à la ligne entre chaque élément d'une liste si on l'affiche.
-
Autocomplétion avec la touche
 : L'autocomplétion trouve les variables qui ont été déclarées.
: L'autocomplétion trouve les variables qui ont été déclarées.- Elle trouve les mots clés et les fonctions locales.
- La complétion des méthodes sur les variables tient compte du type actuel de cette dernière.
- Par contre la complétion ne tient pas compte du contexte.
-
Historique persistant (même si on quitte l'interpréteur, on peut retrouver les dernières commandes par l'historique).
- Recherche dans l'historique avec les flèches du clavier.
- Isole dans l'historique les entrées multilignes.
- On peut appeler les entrées et sorties précédentes.
- Contient des raccourcis et des alias. On peut en afficher la liste en tapant la commande lsmagic.
- Permet d'exécuter des commandes système en les préfixant par un point d'exclamation. Par exemple !ls sous Linux ou OSX, ou !dir sous une fenêtre de commande Windows.
6-3-3. La bibliothèque NumPy▲
6-3-3-a. Introduction▲
Le module numpy est la boîte à outils indispensable pour faire du calcul scientifique avec Python(18).
Pour modéliser les vecteurs, matrices et, plus généralement, les tableaux à n dimensions, numpy fournit le type ndarray.
On note des différences majeures avec les listes (resp. les listes de listes) qui pourraient elles aussi nous servir à représenter des vecteurs (resp. des matrices) :
- les tableaux numpy sont homogènes, c'est-à-dire constitués d'éléments du même type.
On trouvera donc des tableaux d'entiers, des tableaux de flottants, des tableaux de chaînes de caractères, etc. ; - la taille des tableaux numpy est fixée à la création. On ne peut donc augmenter ou diminuer la taille d'un tableau comme on le ferrait pour une liste (à moins de créer un tout nouveau tableau, bien sûr).
Ces contraintes sont en fait des avantages :
- le format d'un tableau numpy et la taille des objets qui le composent étant fixés, l'empreinte du tableau en mémoire est invariable et l'accès à ses éléments se fait en temps constant ;
- les opérations sur les tableaux sont optimisées en fonction du type des éléments, et sont beaucoup plus rapides qu'elles ne le seraient sur des listes équivalentes.
6-3-3-b. Exemples▲
Dans ce premier exemple, on définit un tableau a d'entiers puis on le multiplie globalement, c'est-à-dire sans utiliser de boucle, par le scalaire 2.5. On définit de même le tableau d qui est affecté en une seule instruction à a + b.
In [1]: import numpy as np
In [2]: a = np.array([1, 2, 3, 4])
In [3]: a # a est un tableau d'entiers
Out[3]: array([1, 2, 3, 4])
In [4]: b = a * 2.5
In [5]: b # b est bien devenu un tableau de flottants
Out[5]: array([ 2.5, 5. , 7.5, 10. ])
In [6]: c = np.array([5, 6, 7, 8])
In [7]: d = b + c
In [8]: d # transtypage en flottants
Out[8]: array([ 7.5, 11. , 14.5, 18. ])L'exemple suivant définit un tableau positions de 10 000 000 lignes et 2 colonnes, formant des positions aléatoires. Les vecteurs colonnes x et y sont extraits du tableau position. On affiche le tableau et le vecteur x avec 3 chiffres après le point décimal. On calcule (bien sûr globalement) le vecteur des distances euclidiennes à un point particulier kitxmlcodeinlinelatexdvp\left ( x_{0}, y_{0}\right )finkitxmlcodeinlinelatexdvp et on affiche l'indice du tableau de la distance minimale à ce point.
In [1]: import numpy as np
In [2]: positions = np.random.rand(10000000, 2)
In [3]: x, y = positions[:, 0], positions[:, 1]
In [4]: %precision 3
Out[4]: '%.3f'
In [5]: positions
Out[5]:
array([[ 0.861, 0.373],
[ 0.627, 0.935],
[ 0.224, 0.058],
...,
[ 0.628, 0.66 ],
[ 0.546, 0.416],
[ 0.396, 0.625]])
In [6]: x
Out[6]: array([ 0.861, 0.627, 0.224, ..., 0.628, 0.546, 0.396])
In [7]: x0, y0 = 0.5, 0.5
In [8]: distances = (x - x0)**2 + (y - y0)**2
In [9]: distances.argmin()
Out[9]: 4006531Ce type de traitement très efficace et élégant est typique des logiciels analogues comme MATLAB.
6-3-4. La bibliothèque matplotlib▲
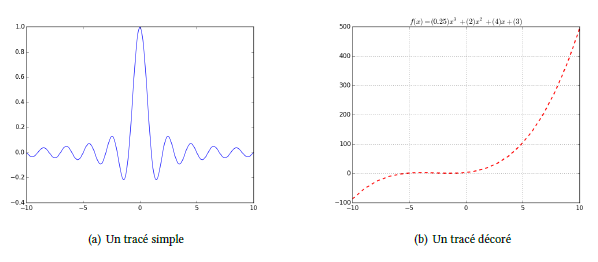
Cette bibliothèque permet toutes sortes de représentations(19) de graphes 2D (et quelques-unes en 3D) :
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10, 10, 200)
y = np.sin(np.pi * x)/(np.pi * x)
plt.plot(x, y)
plt.show()Ce second exemple améliore le tracé. Il utilise le style objet de matplotlib :
import numpy as np
import matplotlib.pyplot as plt
def plt_arrays(x, y, title='', color='red', linestyle='dashed', linewidth=2) :
"""Définition des caractéristiques et affichage d'un tracé y(x)."""
fig = plt.figure()
axes = fig.add_subplot(111)
axes.plot(x, y, color=color, linestyle=linestyle, linewidth=linewidth)
axes.set_title(title)
axes.grid()
plt.show()
def f(a, b, c, d) :
x = np.linspace(-10, 10, 20)
y = a*(x**3) + b*(x**2) + c*x + d
title = '$f(x) = (%s)x^3 + (%s)x^2 + (%s)x + (%s)$' % (a, b, c, d)
plt_arrays(x, y, title=title)
f(0.25, 2, 4, 3)6-3-5. La bibliothèque SymPy▲
6-3-5-a. Introduction▲
SymPy est une bibliothèque en pur Python spécialisée dans le calcul formel à l'instar de Maple ou Mathematica(20). Elle permet de faire du calcul arithmétique formel basique, de l'algèbre, des mathématiques différentielles, de la physique, de la mécanique…
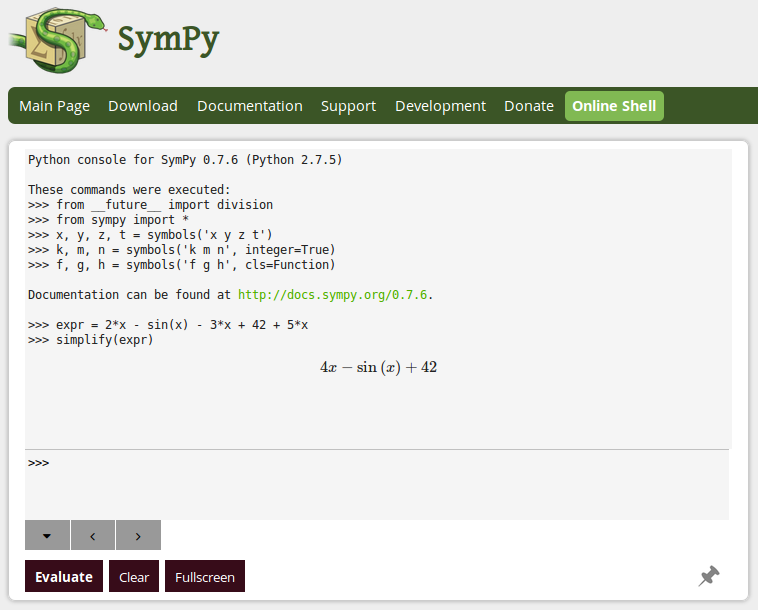
Il est facile de se familiariser avec SymPy en l'expérimentant directement sur Internet(21).
6-3-5-b. Exemples▲
Si l'interpréteur IPython est déjà installé, une alternative intéressante est fournie par le script isympy. Voici quelques exemples des très nombreuses possibilités offertes par cette bibliothèque :
In [1]: P = (x-1) * (x-2) * (x-3)
In [2]: P.expand()
Out[2]:
3 2
x - 6?x + 11?x - 6
In [3]: P.factor()
Out[3]: (x - 3)?(x - 2)?(x - 1)
In [4]: roots = solve(P, x)
In [5]: roots
Out[5]: [1, 2, 3]
In [6]: sin(pi/6)
Out[6]: 1/2
In [7]: cos(pi/6)
Out[7]:
___
?? 3
?????
2
In [8]: tan(pi/6)
Out[8]:
___
?? 3
?????
3
In [9]: e = 2*sin(x)**2 + 2*cos(x)**2
In [10]: trigsimp(e)
Out[10]: 2
In [11]: z = 4 + 3*I
In [12]: Abs(z)
Out[12]: 5
In [13]: arg(z)
Out[13]: atan(3/4)
In [14]: f = x**2 * sin(x)
In [15]: diff(f, x)
Out[15]:
2
x ?cos(x) + 2?x?sin(x)6-4. Bibliothèques tierces▲
6-4-1. Une grande diversité▲
Outre les nombreux modules intégrés à la distribution standard de Python, on trouve des bibliothèques dans tous les domaines :
- scientifique ;
- bases de données ;
- tests fonctionnels et contrôle de qualité ;
- 3D ;
- …
Le site pypi.python.org/pypi(22) recense des milliers de modules et de packages !
6-4-2. Un exemple : la bibliothèque Unum▲
Cette bibliothèque permet de calculer en tenant compte des unités du système SI (Système International d'unités).
Voici un exemple de session interactive :
>>> from unum.units import *
>>> distance = 100*m
>>> temps = 9.683*s
>>> vitesse = distance / temps
>>> vitesse
10.327377878756584 [m/s]
>>> vitesse.asUnit(mile/h)
23.1017437978 [mile/h]
>>> acceleration = vitesse/temps
>>> acceleration
1.0665473385063085 [m/s2]6-5. Packages▲
Outre le module, un deuxième niveau d'organisation permet de structurer le code : les fichiers Python peuvent être organisés en une arborescence de répertoires appelée paquet, en anglais package.
Un package est un module contenant d'autres modules. Les modules d'un package peuvent être des sous-packages, ce qui donne une structure arborescente.
Pour être reconnu comme un package valide, chaque répertoire du paquet doit posséder un fichier __init__ qui peut soit être vide soit contenir du code d'initialisation.