Chapitre 15 : Analyse de programmes concrets▲
Dans ce chapitre, nous allons nous efforcer d'illustrer la démarche de conception d'un
programme graphique, depuis ses premičres ébauches jusqu'ŕ un stade de développement
relativement avancé. Nous souhaitons montrer ainsi combien la programmation orientée objet peut
faciliter et surtout sécuriser la stratégie de développement incrémental que nous préconisons58.
L'utilisation de classes s'impose, lorsque l'on constate qu'un projet en cours de réalisation se
révčle nettement plus complexe que ce que l'on avait imaginé au départ. Vous vivrez certainement
vous-męme des cheminements similaires ŕ celui que nous décrivons ci-dessous.
15.1. Jeu des bombardes▲
Ce projet de jeu59 s'inspire d'un travail similaire réalisé par des élčves de terminale.
Il est vivement recommandé de commencer l'ébauche d'un tel projet par une série de petits
dessins et de schémas, dans lesquels seront décrits les différents éléments graphiques ŕ construire,
ainsi qu'un maximum de cas d'utilisations. Si vous rechignez ŕ utiliser pour cela la bonne vieille
technologie papier/crayon (laquelle a pourtant bien fait ses preuves), vous pouvez tirer profit d'un
logiciel de dessin technique, tel l'utilitaire Draw de la suite bureautique OpenOffice.org60. C'est
l'outil qui a été utilisé pour réaliser le schéma ci-dessous :
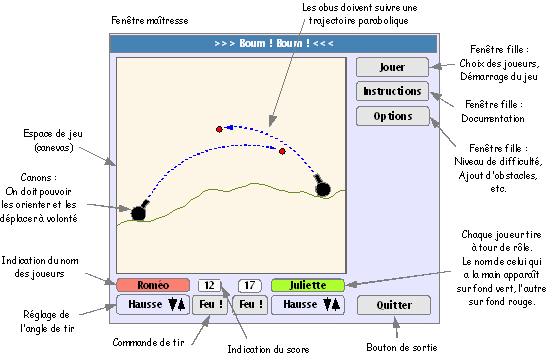
L'idée de départ est simple : deux joueurs s'affrontent au canon. Chacun doit ajuster son angle de
tir pour tâcher d'atteindre son adversaire, les obus décrivant une trajectoire balistique.
L'emplacement des canons est défini au début du jeu de maničre aléatoire (tout au moins en
hauteur). Aprčs chaque tir, les canons se déplacent (afin d'accroître l'intéręt du jeu, l'ajustement des
tirs étant ainsi rendu plus difficile). Les coups au but sont comptabilisés.
Le dessin préliminaire que nous avons reproduit ŕ la page précédente est l'une des formes que
peut prendre votre travail d'analyse. Avant de commencer le développement d'un projet de
programmation, il vous faut en effet toujours vous efforcer d'établir un cahier des charges détaillé.
Cette étude préalable est trčs importante. La plupart des débutants commencent bien trop vite ŕ
écrire de nombreuses lignes de code au départ d'une vague idée, en négligeant de rechercher la
structure d'ensemble. Leur programmation risque alors de devenir chaotique, parce qu'ils devront de
toute façon mettre en place cette structure tôt ou tard. Il s'apercevront alors bien souvent qu'il leur
faut supprimer et ré-écrire des pans entiers d'un projet qu'ils ont conçu d'une maničre trop
monolithique et/ou mal paramétrée.
- Trop monolithique : cela signifie que l'on a négligé de décomposer un problčme complexe en
plusieurs sous-problčmes plus simples. Par exemple, on a imbriqué plusieurs niveaux successifs
d'instructions composées, au lieu de faire appel ŕ des fonctions ou ŕ des classes.
- Mal paramétrée : cela signifie que l'on a traité seulement un cas particulier, au lieu d'envisager le cas général. Par exemple, on a donné ŕ un objet graphique des dimensions fixes, au lieu de prévoir des variables pour permettre son redimensionnement.
Vous devez donc toujours commencer le développement d'un projet par une phase d'analyse
aussi fouillée que possible, et concrétiser le résultat de cette analyse dans un ensemble de
documents (schémas, plans, descriptions...) qui constitueront le cahier des charges. Pour les projets
de grande envergure, il existe d'ailleurs des méthodes d'analyse trčs élaborées (UML, Merise...) que
nous ne pouvons nous permettre de décrire ici car elles font l'objet de livres entiers.
Cela étant dit, il faut malheureusement admettre qu'il est trčs difficile (et męme probablement
impossible) de réaliser dčs le départ l'analyse tout ŕ fait complčte d'un projet de programmation.
C'est seulement lorsqu'il commence ŕ fonctionner véritablement qu'un programme révčle ses
faiblesses. On constate alors qu'il reste des cas d'utilisation ou des contraintes qui n'avaient pas été
prévues au départ. D'autre part, un projet logiciel est pratiquement toujours destiné ŕ évoluer : il
vous arrivera fréquemment de devoir modifier le cahier des charges au cours du développement luimęme,
pas nécessairement parce que l'analyse initiale a été mal faite, mais tout simplement parce
que l'on souhaite encore ajouter des fonctionnalités supplémentaires.
En conclusion, tâchez de toujours aborder un nouveau projet de programmation en respectant les
deux consignes suivantes :
- Décrivez votre projet en profondeur avant de commencer la rédaction des premičres lignes de
code, en vous efforçant de mettre en évidence les composants principaux et les relations qui les
lient (pensez notamment ŕ décrire les différents cas d'utilisation de votre programme)
- Lorsque vous commencerez sa réalisation effective, évitez de vous laisser entraîner ŕ rédiger de
trop grands blocs d'instructions. Veillez au contraire ŕ découper votre application en un certain
nombre de composants paramétrables bien encapsulés, de telle maničre que vous puissiez
aisément modifier l'un ou l'autre d'entre eux sans compromettre le fonctionnement des autres, et
peut-ętre męme les réutiliser dans différents contextes si le besoin s'en fait sentir.
C'est pour satisfaire cette exigence que la programmation orientée objets est a été inventée.
Considérons par exemple l'ébauche dessinée ŕ la page précédente.
L'apprenti programmeur sera peut-ętre tenté de commencer la réalisation de ce jeu en n'utilisant
que la programmation procédurale seule (c'est-ŕ-dire en omettant de définir de nouvelles classes).
C'est d'ailleurs ainsi que nous avons procédé nous-męme lors de notre premičre approche des
interfaces graphiques, tout au long du chapitre 8. Cette façon de procéder ne se justifie cependant
que pour de tout petits programmes (des exercices ou des tests préliminaires). Lorsque l'on s'attaque
ŕ un projet d'une certaine importance, la complexité des problčmes qui se présentent se révčle
rapidement trop importante, et il devient alors indispensable de fragmenter et de compartimenter.
L'outil logiciel qui va permettre cette fragmentation est la classe.
Nous pouvons peut-ętre mieux comprendre son utilité en nous aidant d'une analogie :
Tous les appareils électroniques sont constitués d'un petit nombre de composants de base, ŕ
savoir des transistors, des diodes, des résistances, des condensateurs, etc. Les premiers ordinateurs
ont été construits directement ŕ partir de ces composants. Ils étaient volumineux, trčs chers, et
pourtant ils n'avaient que trčs peu de fonctionnalités et tombaient fréquemment en panne.
On a alors développé différentes techniques pour encapsuler dans un męme boîtier un certain
nombre de composants électroniques de base. Pour utiliser ces nouveaux circuits intégrés, il n'était
plus nécessaire de connaître leur contenu exact : seule importait leur fonction globale. Les
premičres fonctions intégrées étaient encore relativement simples : c'étaient par exemple des portes
logiques, des bascules, etc. En combinant ces circuits entre eux, on obtenait des caractéristiques
plus élaborées, telles que des registres ou des décodeurs, qui purent ŕ leur tour ętre intégrés, et ainsi
de suite, jusqu'aux microprocesseurs actuels. Ceux-ci contiennent dorénavant plusieurs millions de
composants, et pourtant leur fiabilité reste extręmement élevée.
En conséquence, pour l'électronicien moderne qui veut construire par exemple un compteur
binaire (circuit qui nécessite un certain nombre de bascules), il est évidemment bien plus simple,
plus rapide et plus sűr de se servir de bascules intégrées, plutôt que de s'échiner ŕ combiner sans
erreur plusieurs centaines de transistors et de résistances.
D'une maničre analogue, le programmeur moderne que vous ętes peut bénéficier du travail
accumulé par ses prédécesseurs en utilisant la fonctionnalité intégrée dans les nombreuses
bibliothčques de classes déjŕ disponibles pour Python. Mieux encore, il peut aisément créer luimęme
de nouvelles classes pour encapsuler les principaux composants de son application,
particuličrement ceux qui y apparaissent en plusieurs exemplaires. Procéder ainsi est plus simple,
plus rapide et plus sűr que de multiplier les blocs d'instructions similaires dans un corps de
programme monolithique, de plus en plus volumineux et de moins en moins compréhensible.
Examinons par exemple notre ébauche dessinée. Les composants les plus importants de ce jeu
sont bien évidemment les petits canons, qu'il faudra pouvoir dessiner ŕ différents emplacements et
dans différentes orientations, et dont il nous faudra au moins deux exemplaires.
Plutôt que de les dessiner morceau par morceau dans le canevas au fur et ŕ mesure du
déroulement du jeu, nous avons intéręt ŕ les considérer comme des objets logiciels ŕ part entičre,
dotés de plusieurs propriétés ainsi que d'un certain comportement (ce que nous voulons exprimer
par lŕ est le fait qu'il devront ętre dotés de divers mécanismes, que nous pourrons activer par
programme ŕ l'aide de méthodes particuličres). Il est donc certainement judicieux de leur consacrer
une classe spécifique
58 Voir page 16 : Recherche des erreurs et expérimentation, et aussi page 216 : Fenętres avec menus
59 Nous n'hésitons pas ŕ discuter ici le développement d'un logiciel de jeu, parce qu'il s'agit d'un domaine directement
accessible ŕ tous, et dans lequel les objectifs concrets sont aisément identifiables. Il va de soi que les męmes
techniques de développement peuvent s'appliquer ŕ d'autres applications plus "sérieuses".
60 Il s'agit d'une suite bureautique complčte, libre et gratuite, largement compatible avec MS-Office, disponible pour
Linux, Windows, MacOS, Solaris ... Le présent manuel a été entičrement rédigé avec son traitement de textes.
Vous pouvez vous la procurer par téléchargement depuis le site Web : http://www.openoffice.org
15.1.1. Prototypage d'une classe « Canon »▲
En définissant une telle classe, nous gagnons sur plusieurs tableaux. Non seulement nous
rassemblons ainsi tout le code correspondant au dessin et au fonctionnement du canon dans une
męme « capsule », bien ŕ l'écart du reste du programme, mais de surcroît nous nous donnons la
possibilité d'instancier aisément un nombre quelconque de ces canons dans le jeu, ce qui nous ouvre
des perspectives de développements ultérieurs.
Lorsqu'une premičre implémentation de la classe Canon() aura été construite et testée, il sera
également possible de la perfectionner en la dotant de caractéristiques supplémentaires, sans
modifier (ou trčs peu) son interface, c'est-ŕ-dire en quelque sorte son « mode d'emploi » : ŕ savoir
les instructions nécessaires pour l'instancier et l'utiliser dans des applications diverses.
Entrons ŕ présent dans le vif du sujet.
Le dessin de notre canon peut ętre simplifié ŕ l'extręme. Nous avons estimé qu'il pouvait se
résumer ŕ un cercle combiné avec un rectangle, celui-ci pouvant d'ailleurs ętre lui-męme considéré
comme un simple segment de ligne droite particuličrement épais.
Si l'ensemble est rempli d'une couleur uniforme (en noir, par exemple), nous obtiendrons ainsi
une sorte de petite bombarde suffisamment crédible.
| Dans la suite du raisonnement, nous admettrons que la position
du canon est en fait la position du centre du cercle (coordonnées x
et y dans le dessin ci-contre). Ce point clé indique également l'axe
de rotation de la buse du canon, ainsi que l'une des extrémités de la
ligne épaisse qui représentera cette buse. Pour terminer notre dessin, il nous restera alors ŕ déterminer les coordonnées de l'autre extrémité de cette ligne. Ces coordonnées peuvent ętre calculées sans grande difficulté, ŕ la condition de nous remémorer deux concepts fondamentaux de la trigonométrie (le sinus et le cosinus) que vous devez certainement bien connaître : |

|
| Dans un triangle rectangle, le rapport entre le coté opposé ŕ un
angle et l'hypoténuse du triangle est une propriété spécifique de cet
angle qu'on appelle sinus de l'angle. Le cosinus du męme angle est
le rapport entre le côté adjacent ŕ l'angle et l'hypoténuse. Ainsi, dans le schéma ci-contre : 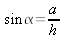 et et 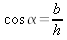 |
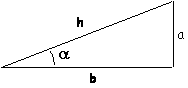
|
Pour représenter la buse de notre canon, en supposant que nous connaissions sa longueur l et
l'angle de tir \x{03b1} , il nous faut donc tracer un segment de ligne droite épaisse, ŕ partir des coordonnées
du centre du cercle (x et y), jusqu'ŕ un autre point situé plus ŕ droite et plus haut, l'écart horizontal
\x{0394}x étant égal ŕ l.cos \x{03b1} , et l'écart vertical \x{0394}y étant égal ŕ l.sin \x{03b1} .
En résumant tout ce qui précčde, dessiner un canon au point x, y consistera simplement ŕ :
- tracer un cercle noir centré sur x, y
- tracer une ligne noire épaisse depuis le point x, y jusqu'au point x + l.cos \x{03b1}, y + l.sin \x{03b1}.
Nous pouvons ŕ présent commencer ŕ envisager une ébauche de programmation correspondant ŕ
une classe « Canon ». Il n'est pas encore question ici de programmer le jeu proprement dit. Nous
voulons seulement vérifier si l'analyse que nous avons faite jusqu'ŕ présent « tient la route », en
réalisant un premier prototype fonctionnel.
Un prototype est un petit programme destiné ŕ expérimenter une idée, que l'on se propose
d'intégrer ensuite dans une application plus vaste. Du fait de sa simplicité et de sa concision, Python
se pręte fort bien ŕ l'élaboration de prototypes, et de nombreux programmeurs l'utilisent pour mettre
au point divers composants logiciels qu'ils reprogrammeront éventuellement ensuite dans d'autres
langages plus « lourds », tels que le C par exemple.
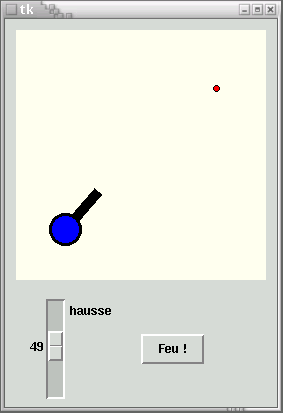
Dans notre premier prototype, la classe Canon() ne comporte que deux méthodes : un
constructeur qui crée les éléments de base du dessin, et une méthode permettant de modifier celui-ci
ŕ volonté pour ajuster l'angle de tir (l'inclinaison de la buse). Comme nous l'avons souvent fait dans
d'autres exemples, nous inclurons quelques lignes de code ŕ la fin du script afin de pouvoir tester la
classe tout de suite :
1. from Tkinter import *
2. from math import pi, sin, cos
3.
4. class Canon:
5. """Petit canon graphique"""
6. def __init__(self, boss, x, y):
7. self.boss = boss # référence du canevas
8. self.x1, self.y1 = x, y # axe de rotation du canon
9. # dessiner la buse du canon, ŕ l'horizontale pour commencer :
10. self.lbu = 50 # longueur de la buse
11. self.x2, self.y2 = x + self.lbu, y
12. self.buse = boss.create_line(self.x1, self.y1, self.x2, self.y2,
13. width =10)
14. # dessiner ensuite le corps du canon par-dessus :
15. r = 15 # rayon du cercle
16. boss.create_oval(x-r, y-r, x+r, y+r, fill='blue', width =3)
17.
18. def orienter(self, angle):
19. "choisir l'angle de tir du canon"
20. # rem : le paramčtre <angle> est reçu en tant que chaîne de car.
21. # il faut le traduire en nombre réel, puis convertir en radians :
22. self.angle = float(angle)*2*pi/360
23. self.x2 = self.x1 + self.lbu*cos(self.angle)
24. self.y2 = self.y1 - self.lbu*sin(self.angle)
25. self.boss.coords(self.buse, self.x1, self.y1, self.x2, self.y2)
26.
27.if __name__ == '__main__':
28. # Code pour tester sommairement la classe Canon :
29. f = Tk()
30. can = Canvas(f,width =250, height =250, bg ='ivory')
31. can.pack(padx =10, pady =10)
32. c1 = Canon(can, 50, 200)
33.
34. s1 =Scale(f, label='hausse', from_=90, to=0, command=c1.orienter)
35. s1.pack(side=LEFT, pady =5, padx =20)
36. s1.set(25) # angle de tir initial
37.
38. f.mainloop()
Commentaires :
- Ligne 6 : Dans la liste des paramčtres qui devront ętre transmis au constructeur lors de
l'instanciation, nous prévoyons les coordonnées x et y, qui indiqueront l'emplacement du canon
dans le canevas, mais également une référence au canevas lui-męme (la variable boss). Cette
référence est indispensable : elle sera utilisée pour invoquer les méthodes du canevas.
Nous pourrions inclure aussi un paramčtre pour choisir un angle de tir initial, mais puisque nous avons l'intention d'implémenter une méthode spécifique pour régler cette orientation, il sera plus judicieux de faire appel ŕ celle-ci au moment voulu. - Lignes 7 et 8 : Ces références seront utilisées un peu partout dans les différentes méthodes que
nous allons développer dans la classe. Il faut donc en faire des attributs d'instance.
- Lignes 9 ŕ 16 : Nous dessinons la buse d'abord, et le corps du canon ensuite. Ainsi une partie de
la buse reste cachée. Cela nous permet de colorer éventuellement le corps du canon.
- Lignes 18 ŕ 25 : Cette méthode sera invoquée avec un argument « angle », lequel sera fourni en
degrés (comptés ŕ partir de l'horizontale). S'il est produit ŕ l'aide d'un widget tel que Entry ou
Scale, il sera transmis sous la forme d'une chaîne de caractčres, et nous devrons donc le convertir
d'abord en nombre réel avant de l'utiliser dans nos calculs (ceux-ci ont été décrits ŕ la page
précédente).
- Lignes 27 ŕ 38 : Pour tester notre nouvelle classe, nous ferons usage d'un widget Scale. Pour définir la position initiale de son curseur, et donc fixer l'angle de hausse initial du canon, nous devons faire appel ŕ sa méthode set() (ligne 36).
15.1.2. Ajout de méthodes au prototype▲
| Notre prototype est fonctionnel, mais beaucoup trop
rudimentaire. Nous devons ŕ présent le perfectionner pour lui
ajouter la capacité de tirer des obus. Ceux-ci seront traités plutôt comme des « boulets » : ce seront de simples petits cercles que nous ferons partir de la bouche du canon avec une vitesse initiale d'orientation identique ŕ celle de sa buse. Pour leur faire suivre une trajectoire réaliste, nous devons ŕ présent nous replonger dans notre cours de physique : Comment un objet laissé ŕ lui-męme évolue-t-il dans l'espace, si l'on néglige les phénomčnes secondaires tels que la résistance de l'air ? Ce problčme peut vous paraître complexe, mais en réalité sa résolution est trčs simple : il vous suffit d'admettre que le boulet se déplace ŕ la fois horizontalement et verticalement, et que ces deux mouvements simultanés sont tout ŕ fait indépendants l'un de l'autre. Vous allez donc établir une boucle d'animation dans laquelle vous recalculez les nouvelles coordonnées x et y du boulet ŕ intervalles de temps réguliers, en sachant que : |
|
- Le mouvement horizontal est uniforme. Ŕ chaque itération, il vous suffit d'augmenter
graduellement la coordonnée x du boulet, en lui ajoutant toujours un męme déplacement \x{0394}x.
- Le mouvement vertical est uniformément accéléré. Cela signifie simplement qu'ŕ chaque itération, vous devez ajouter ŕ la coordonnée y un déplacement Dy qui augmente lui-męme graduellement, toujours de la męme quantité.
Voyons cela dans le script :
A) Pour commencer, il faut ajouter les lignes suivantes ŕ la fin de la méthode constructeur. Elles
vont servir ŕ créer l'objet « obus », et ŕ préparer une variable d'instance qui servira d'interrupteur de
l'animation. L'obus est créé au départ avec des dimensions minimales (un cercle d'un seul pixel) afin
de rester presqu'invisible :
# dessiner un obus (réduit ŕ un simple point, avant animation) :
self.obus =boss.create_oval(x, y, x, y, fill='red')
self.anim =False # interrupteur d'animation
# retrouver la largeur et la hauteur du canevas :
self.xMax =int(boss.cget('width'))
self.yMax =int(boss.cget('height'))
Les deux derničres lignes utilisent la méthode cget() du widget « maître » (le canevas, ici), afin
de retrouver certaines de ses caractéristiques. Nous voulons en effet que notre classe Canon soit
généraliste, c'est-ŕ-dire réutilisable dans n'importe quel contexte, et nous ne pouvons donc pas
tabler ŕ l'avance sur des dimensions particuličres pour le canevas dans lequel ce canon sera utilisé.
Note : Tkinter renvoie ces valeurs sous la forme de chaînes de caractčres. Il faut donc les convertir
dans un type numérique si nous voulons pouvoir les utiliser dans un calcul.
B) Ensuite, nous devons ajouter deux nouvelles méthodes : l'une pour déclencher le tir, et l'autre
pour gérer l'animation du boulet une fois que celui-ci aura été lancé :
1. def feu(self):
2. "déclencher le tir d'un obus"
3. if not self.anim:
4. self.anim =True
5. # position de départ de l'obus (c'est la bouche du canon) :
6. self.boss.coords(self.obus, self.x2 -3, self.y2 -3,
7. self.x2 +3, self.y2 +3)
8. v =15 # vitesse initiale
9. # composantes verticale et horizontale de cette vitesse :
10. self.vy = -v *sin(self.angle)
11. self.vx = v *cos(self.angle)
12. self.animer_obus()
13.
14. def animer_obus(self):
15. "animation de l'obus (trajectoire balistique)"
16. if self.anim:
17. self.boss.move(self.obus, int(self.vx), int(self.vy))
18. c = self.boss.coords(self.obus) # coord. résultantes
19. xo, yo = c[0] +3, c[1] +3 # coord. du centre de l'obus
20. if yo > self.yMax or xo > self.xMax:
21. self.anim =False # arręter l'animation
22. self.vy += .5
23. self.boss.after(30, self.animer_obus)
Commentaires :
- Lignes 1 ŕ 4 : Cette méthode sera invoquée par appui sur un bouton. Elle déclenche le
mouvement de l'obus, et attribue une valeur « vraie » ŕ notre « interrupteur d'animation » (la
variable self.anim : voir ci-aprčs). Il faut cependant nous assurer que pendant toute la durée de
cette animation, un nouvel appui sur le bouton ne puisse pas activer d'autres boucles d'animation
parasites. C'est le rôle du test effectué ŕ la ligne 3 : le bloc d'instruction qui suit ne peut
s'exécuter que si la variable self.anim possčde la valeur « faux », ce qui signifie que l'animation
n'a pas encore commencé.
- Lignes 5 ŕ 7 : Le canevas Tkinter dispose de deux méthodes pour déplacer les objets graphiques :
La méthode coords() effectue un positionnement absolu ; il faut cependant lui fournir toutes les
coordonnées de l'objet (comme si on le redessinait). La méthode move() , utilisée ŕ la ligne 17,
provoque quant ŕ elle un déplacement relatif ; elle s'utilise avec deux arguments seulement : les
composantes horizontale et verticale du déplacement souhaité.
- Lignes 8 ŕ 12 : La vitesse initiale de l'obus est choisie ŕ la ligne 8. Comme nous l'avons expliqué
ŕ la page précédente, le mouvement du boulet est la résultante d'un mouvement horizontal et d'un
mouvement vertical. Nous connaissons la valeur de la vitesse initiale ainsi que son inclinaison
(c'est-ŕ-dire l'angle de tir). Pour déterminer les composantes horizontale et verticale de cette
vitesse, il nous suffit d'utiliser des relations trigonométriques tout ŕ fait similaires ŕ que celles
que nous avons déjŕ exploitées pour dessiner la buse du canon. Le signe - utilisé ŕ la ligne 9
provient du fait que les coordonnées verticales se comptent de haut en bas.
La ligne 12 active l'animation proprement dite. - Lignes 14 ŕ 23 : Cette procédure se ré-appelle elle-męme toutes les 30 millisecondes par
l'intermédiaire de la méthode after() invoquée ŕ la ligne 23. Cela continue aussi longtemps que
la variable self.anim (notre « interrupteur d'animation ») reste « vraie », condition qui changera
lorsque les coordonnées de l'obus sortiront des limites imposées (test de la ligne 20).
- Lignes 18, 19 : Pour retrouver ces coordonnées aprčs chaque déplacement, on fait appel encore
une fois ŕ la méthode coords() du canevas : utilisée avec la référence d'un objet graphique
comme unique argument, elle renvoie ses quatre coordonnées dans un tuple.
- Lignes 17 et 22 : La coordonnée horizontale de l'obus augmente toujours de la męme quantité
(mouvement uniforme), tandis que la coordonnée verticale augmente d'une quantité qui est ellemęme
augmentée ŕ chaque fois ŕ la ligne 24 (mouvement uniformément accéléré). Le résultat est
une trajectoire parabolique.
Rappel : l'opérateur += permet d'incrémenter une variable : « a += 3 » équivaut ŕ « a = a + 3 ». -
C) Il reste enfin ŕ ajouter un bouton déclencheur dans la fenętre principale. Une ligne telle que la suivante (ŕ insérer dans le code de test) fera parfaitement l'affaire :
Button(f, text='Feu !', command =c1.feu).pack(side=LEFT)
15.1.3. Développement de l'application▲
Disposant désormais d'une classe d'objets « canon » assez bien dégrossie, nous pouvons ŕ présent envisager l'élaboration de l'application proprement dite. Et puisque nous sommes décidés ŕ exploiter la méthodologie de la programmation orientée objet, nous devons concevoir cette application comme un ensemble d'objets qui interagissent par l'intermédiaire de leurs méthodes.
Plusieurs de ces objets proviendront de classes préexistantes, bien entendu : ainsi le canevas, les
boutons, etc. Mais nous avons vu dans les pages précédentes que nous avons intéręt ŕ regrouper des
ensembles bien délimités de ces objets basiques dans de nouvelles classes, chaque fois que nous
pouvons identifier pour ces ensembles une fonctionnalité particuličre. C'était le cas par exemple
pour cet ensemble de cercles et de lignes mobiles que nous avons décidé d'appeler « canon ».
Pouvons-nous encore distinguer dans notre projet initial d'autres composants qui mériteraient
d'ętre encapsulés dans des nouvelles classes ? Certainement. Il y a par exemple le pupitre de
contrôle que nous voulons associer ŕ chaque canon : nous pouvons y rassembler le dispositif de
réglage de la hausse (l'angle de tir), le bouton de mise ŕ feu, le score réalisé, et peut-ętre d'autres
indications encore, comme le nom du joueur, par exemple. Il est d'autant plus intéressant de lui
consacrer une classe particuličre, que nous savons d'emblée qu'il nous en faudra deux instances.
Il y a aussi l'application elle-męme, bien sűr. En l'encapsulant dans une classe, nous en ferons
notre objet principal, celui qui dirigera tous les autres.
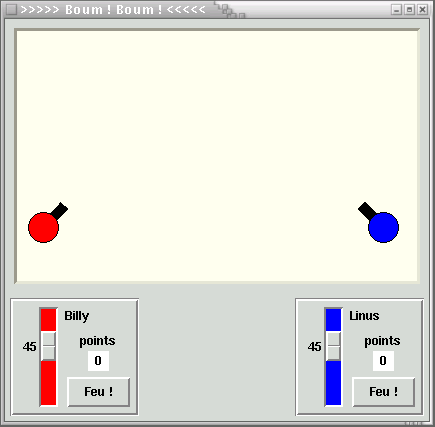
Veuillez ŕ présent analyser le script ci-dessous. Vous y retrouverez la classe Canon() encore
davantage développée : nous y avons ajouté quelques attributs et trois méthodes supplémentaires,
afin de pouvoir gérer les déplacements du canon lui-męme, ainsi que les coups au but.
La classe Application() remplace désormais le code de test des prototypes précédents. Nous y
instancions deux objets Canon(), et deux objets de la nouvelle classe Pupitre(), que nous plaçons
dans des dictionnaires en prévision de développements ultérieurs (nous pouvons en effet imaginer
d'augmenter le nombre de canons et donc de pupitres). Le jeu est ŕ présent fonctionnel : les canons
se déplacent aprčs chaque tir, et les coups au but sont comptabilisés.
1. from Tkinter import *
2. from math import sin, cos, pi
3. from random import randrange
4.
5. class Canon:
6. """Petit canon graphique"""
7. def __init__(self, boss, id, x, y, sens, coul):
8. self.boss = boss # réf. du canevas
9. self.appli = boss.master # réf. de la fenętre d'application
10. self.id = id # identifiant du canon (chaîne)
11. self.coul = coul # couleur associée au canon
12. self.x1, self.y1 = x, y # axe de rotation du canon
13. self.sens = sens # sens de tir (-1:gauche, +1:droite)
14. self.lbu = 30 # longueur de la buse
15. self.angle = 0 # hausse par défaut (angle de tir)
16. # retrouver la largeur et la hauteur du canevas :
17. self.xMax = int(boss.cget('width'))
18. self.yMax = int(boss.cget('height'))
19. # dessiner la buse du canon (horizontale) :
20. self.x2, self.y2 = x + self.lbu * sens, y
21. self.buse = boss.create_line(self.x1, self.y1,
22. self.x2, self.y2, width =10)
23. # dessiner le corps du canon (cercle de couleur) :
24. self.rc = 15 # rayon du cercle
25. self.corps = boss.create_oval(x -self.rc, y -self.rc, x +self.rc,
26. y +self.rc, fill =coul)
27. # pré-dessiner un obus caché (point en dehors du canevas) :
28. self.obus = boss.create_oval(-10, -10, -10, -10, fill='red')
29. self.anim = False # indicateurs d'animation
30. self.explo = False # et d'explosion
31.
32. def orienter(self, angle):
33. "régler la hausse du canon"
34. # rem: le paramčtre <angle> est reçu en tant que chaîne.
35. # Il faut donc le traduire en réel, puis le convertir en radians :
36. self.angle = float(angle)*pi/180
37. # rem: utiliser la méthode coords de préférence avec des entiers :
38. self.x2 = int(self.x1 + self.lbu * cos(self.angle) * self.sens)
39. self.y2 = int(self.y1 - self.lbu * sin(self.angle))
40. self.boss.coords(self.buse, self.x1, self.y1, self.x2, self.y2)
41.
42. def deplacer(self, x, y):
43. "amener le canon dans une nouvelle position x, y"
44. dx, dy = x -self.x1, y -self.y1 # valeur du déplacement
45. self.boss.move(self.buse, dx, dy)
46. self.boss.move(self.corps, dx, dy)
47. self.x1 += dx
48. self.y1 += dy
49. self.x2 += dx
50. self.y2 += dy
51.
52. def feu(self):
53. "tir d'un obus - seulement si le précédent a fini son vol"
54. if not (self.anim or self.explo):
55. self.anim =True
56. # récupérer la description de tous les canons présents :
57. self.guns = self.appli.dictionnaireCanons()
58. # position de départ de l'obus (c'est la bouche du canon) :
59. self.boss.coords(self.obus, self.x2 -3, self.y2 -3,
60. self.x2 +3, self.y2 +3)
61. v = 17 # vitesse initiale
62. # composantes verticale et horizontale de cette vitesse :
63. self.vy = -v *sin(self.angle)
64. self.vx = v *cos(self.angle) *self.sens
65. self.animer_obus()
66. return True # => signaler que le coup est parti
67. else:
68. return False # => le coup n'a pas pu ętre tiré
69.
70. def animer_obus(self):
71. "animer l'obus (trajectoire balistique)"
72. if self.anim:
73. self.boss.move(self.obus, int(self.vx), int(self.vy))
74. c = self.boss.coords(self.obus) # coord. résultantes
75. xo, yo = c[0] +3, c[1] +3 # coord. du centre de l'obus
76. self.test_obstacle(xo, yo) # a-t-on atteint un obstacle ?
77. self.vy += .4 # accélération verticale
78. self.boss.after(20, self.animer_obus)
79. else:
80. # animation terminée - cacher l'obus et déplacer les canons :
81. self.fin_animation()
82.
83. def test_obstacle(self, xo, yo):
84. "évaluer si l'obus a atteint une cible ou les limites du jeu"
85. if yo >self.yMax or xo <0 or xo >self.xMax:
86. self.anim =False
87. return
88. # analyser le dictionnaire des canons pour voir si les coord.
89. # de l'un d'entre eux sont proches de celles de l'obus :
90. for id in self.guns: # id = clef dans dictionn.
91. gun = self.guns[id] # valeur correspondante
92. if xo < gun.x1 +self.rc and xo > gun.x1 -self.rc \
93. and yo < gun.y1 +self.rc and yo > gun.y1 -self.rc :
94. self.anim =False
95. # dessiner l'explosion de l'obus (cercle jaune) :
96. self.explo = self.boss.create_oval(xo -12, yo -12,
97. xo +12, yo +12, fill ='yellow', width =0)
98. self.hit =id # référence de la cible touchée
99. self.boss.after(150, self.fin_explosion)
100. break
101.
102. def fin_explosion(self):
103. "effacer l'explosion ; ré-initaliser l'obus ; gérer le score"
104. self.boss.delete(self.explo) # effacer l'explosion
105. self.explo =False # autoriser un nouveau tir
106. # signaler le succčs ŕ la fenętre maîtresse :
107. self.appli.goal(self.id, self.hit)
108.
109. def fin_animation(self):
110. "actions ŕ accomplir lorsque l'obus a terminé sa trajectoire"
111. self.appli.disperser() # déplacer les canons
112. # cacher l'obus (en l'expédiant hors du canevas) :
113. self.boss.coords(self.obus, -10, -10, -10, -10)
114.
115.
116.class Pupitre(Frame):
117. """Pupitre de pointage associé ŕ un canon"""
118. def __init__(self, boss, canon):
119. Frame.__init__(self, bd =3, relief =GROOVE)
120. self.score =0
121. self.appli =boss # réf. de l'application
122. self.canon =canon # réf. du canon associé
123. # Systčme de réglage de l'angle de tir :
124. self.regl =Scale(self, from_ =75, to =-15, troughcolor=canon.coul,
125. command =self.orienter)
126. self.regl.set(45) # angle initial de tir
127. self.regl.pack(side =LEFT)
128. # Étiquette d'identification du canon :
129. Label(self, text =canon.id).pack(side =TOP, anchor =W, pady =5)
130. # Bouton de tir :
131. self.bTir =Button(self, text ='Feu !', command =self.tirer)
132. self.bTir.pack(side =BOTTOM, padx =5, pady =5)
133. Label(self, text ="points").pack()
134. self.points =Label(self, text=' 0 ', bg ='white')
135. self.points.pack()
136. # positionner ŕ gauche ou ŕ droite suivant le sens du canon :
137. if canon.sens == -1:
138. self.pack(padx =5, pady =5, side =RIGHT)
139. else:
140. self.pack(padx =5, pady =5, side =LEFT)
141.
142. def tirer(self):
143. "déclencher le tir du canon associé"
144. self.canon.feu()
145.
146. def orienter(self, angle):
147. "ajuster la hausse du canon associé"
148. self.canon.orienter(angle)
149.
150. def attribuerPoint(self, p):
151. "incrémenter ou décrémenter le score, de <p> points"
152. self.score += p
153. self.points.config(text = ' %s ' % self.score)
154.
155.class Application(Frame):
156. '''Fenętre principale de l'application'''
157. def __init__(self):
158. Frame.__init__(self)
159. self.master.title('>>>>> Boum ! Boum ! <<<<<')
160. self.pack()
161. self.jeu = Canvas(self, width =400, height =250, bg ='ivory',
162. bd =3, relief =SUNKEN)
163. self.jeu.pack(padx =8, pady =8, side =TOP)
164.
165. self.guns ={} # dictionnaire des canons présents
166. self.pupi ={} # dictionnaire des pupitres présents
167. # Instanciation de 2 'objets canons (+1, -1 = sens opposés) :
168. self.guns["Billy"] = Canon(self.jeu, "Billy", 30, 200, 1, "red")
169. self.guns["Linus"] = Canon(self.jeu, "Linus", 370,200,-1, "blue")
170. # Instanciation de 2 pupitres de pointage associés ŕ ces canons :
171. self.pupi["Billy"] = Pupitre(self, self.guns["Billy"])
172. self.pupi["Linus"] = Pupitre(self, self.guns["Linus"])
173.
174. def disperser(self):
175. "déplacer aléatoirement les canons"
176. for id in self.guns:
177. gun =self.guns[id]
178. # positionner ŕ gauche ou ŕ droite, suivant sens du canon :
179. if gun.sens == -1 :
180. x = randrange(320,380)
181. else:
182. x = randrange(20,80)
183. # déplacement proprement dit :
184. gun.deplacer(x, randrange(150,240))
185.
186. def goal(self, i, j):
187. "le canon <i> signale qu'il a atteint l'adversaire <j>"
188. if i != j:
189. self.pupi[i].attribuerPoint(1)
190. else:
191. self.pupi[i].attribuerPoint(-1)
192.
193. def dictionnaireCanons(self):
194. "renvoyer le dictionnaire décrivant les canons présents"
195. return self.guns
196.
197.if __name__ =='__main__':
198. Application().mainloop()
Commentaires :
- Ligne 7 : Par rapport au prototype, trois paramčtres ont été ajoutés ŕ la méthode constructeur. Le
paramčtre id nous permet d'identifier chaque instance de la classe Canon() ŕ l'aide d'un nom
quelconque. Le paramčtre sens indique s'il s'agit d'un canon qui tire vers la droite (sens = 1) ou
vers la gauche (sens = -1). Le paramčtre coul spécifie la couleur associée au canon.
- Ligne 9 : Il faut savoir que tous les widgets Tkinter possčdent un attribut master qui contient la
référence leur widget maître éventuel (leur « contenant »). Cette référence est donc pour nous
celle de l'application principale. (Nous avons implémenté nous-męmes une technique similaire
pour référencer le canevas, ŕ l'aide de l'attribut boss).
- Lignes 42 ŕ 50 : Cette méthode permet d'amener le canon dans un nouvel emplacement. Elle
servira ŕ repositionner les canons au hasard aprčs chaque tir, ce qui augmente l'intéręt du jeu.
Note : l'opérateur += permet d'incrémenter une variable : « a += 3 » équivaut ŕ « a = a + 3 ». - Lignes 56, 57 : Nous essayons de construire notre classe canon de telle maničre qu'elle puisse
ętre réutilisée dans des projets plus vastes, impliquant un nombre quelconque d'objets canons qui
pourront apparaître et disparaître au fil des combats. Dans cette perspective, il faut que nous
puissions disposer d'une description de tous les canons présents, avant chaque tir, de maničre ŕ
pouvoir déterminer si une cible a été touchée ou non. Cette description est gérée par l'application
principale, dans un dictionnaire, dont on peut lui demander une copie par l'intermédiaire de sa
méthode dictionnaireCanons().
- Lignes 66 ŕ 68 : Dans cette męme perspective généraliste, il peut ętre utile d'informer
éventuellement le programme appelant que le coup a effectivement été tiré ou non.
- Ligne 76 : L'animation de l'obus est désormais traitée par deux méthodes complémentaires. Afin
de clarifier le code, nous avons placé dans une méthode distincte les instructions servant ŕ
déterminer si une cible a été atteinte (méthode test_obstacle()).
- Lignes 79 ŕ 81 : Nous avons vu précédemment que l'on interrompt l'animation de l'obus en
attribuant une valeur « fausse » ŕ la variable self.anim. La méthode animer_obus() cesse alors
de boucler et exécute le code de la ligne 81.
- Lignes 83 ŕ 100 : Cette méthode évalue si les coordonnées actuelles de l'obus sortent des limites
de la fenętre, ou encore si elles s'approchent de celles d'un autre canon. Dans les deux cas,
l'interrupteur d'animation est actionné, mais dans le second, on dessine une « explosion » jaune,
et la référence du canon touché est mémorisée. La méthode annexe fin_explosion() est invoquée
aprčs un court laps de temps pour terminer le travail, c'est-ŕ-dire effacer le cercle d'explosion et
envoyer un message signalant le coup au but ŕ la fenętre maîtresse.
- Lignes 115 ŕ 153 : La classe Pupitre() définit un nouveau widget par dérivation de la classe
Frame(), selon une technique qui doit désormais vous ętre devenue familičre. Ce nouveau
widget regroupe les commandes de hausse et de tir, ainsi que l'afficheur de points associés ŕ un
canon bien déterminé. La correspondance visuelle entre les deux est assurée par l'adoption d'une
couleur commune. Les méthodes tirer() et orienter() communiquent avec l'objet Canon()
associé, par l'intermédiaire des méthodes de celui-ci.
- Lignes 155 ŕ 172 : La fenętre d'application est elle aussi un widget dérivé de Frame(). Son
constructeur instancie les deux canons et leurs pupitres de pointage, en plaçant ces objets dans
les deux dictionnaires self.guns et self.pupi. Cela permet d'effectuer ensuite divers traitements
systématiques sur chacun d'eux (comme par exemple ŕ la méthode suivante). En procédant ainsi,
on se réserve en outre la possibilité d'augmenter sans effort le nombre de ces canons si
nécessaire, dans les développements ultérieurs du programme.
- Lignes 174 ŕ 184 : Cette méthode est invoquée aprčs chaque tir pour déplacer aléatoirement les deux canons, ce qui augmente la difficulté du jeu.
15.1.4. Développements complémentaires▲
Tel qu'il vient d'ętre décrit, notre programme correspond déjŕ plus ou moins au cahier des
charges initial, mais il est évident que nous pouvons continuer ŕ le perfectionner.
A) Nous devrions par exemple mieux le paramétrer. Qu'est-ce ŕ dire ? Dans sa forme actuelle,
notre jeu comporte un canevas de taille prédéterminée (400 x 250 pixels, voir ligne 161). Si nous
voulons modifier ces valeurs, nous devons veiller ŕ modifier aussi les autres lignes du script oů ces
dimensions interviennent (comme par exemple aux lignes 168-169, ou 179-184). De telles lignes
interdépendantes risquent de devenir nombreuses si nous ajoutons encore d'autres fonctionnalités. Il
serait donc plus judicieux de dimensionner le canevas ŕ l'aide de variables, dont la valeur serait
définie en un seul endroit. Ces variables seraient ensuite exploitées dans toutes les lignes
d'instructions oů les dimensions du canevas interviennent.
Nous avons déjŕ effectué une partie de ce travail : dans la classe Canon(), en effet, les
dimensions du canevas sont récupérées ŕ l'aide d'une méthode prédéfinie (voir lignes 17-18), et
placées dans des attributs d'instance qui peuvent ętre utilisés partout dans la classe.
B) Aprčs chaque tir, nous provoquons un déplacement aléatoire des canons, en redéfinissant
leurs coordonnées au hasard. Il serait probablement plus réaliste de provoquer de véritables
déplacements relatifs, plutôt que de redéfinir au hasard des positions absolues. Pour ce faire, il
suffit de retravailler la méthode deplacer() de la classe Canon(). En fait, il serait encore plus
intéressant de faire en sorte que cette méthode puisse produire ŕ volonté, aussi bien un déplacement
relatif qu'un positionnement absolu, en fonction d'une valeur transmise en argument.
C) Le systčme de commande des tirs devrait ętre amélioré : puisque nous ne disposons que d'une
seule souris, il faut demander aux joueurs de tirer ŕ tour de rôle, et nous n'avons mis en place aucun
mécanisme pour les forcer ŕ le faire. Une meilleure approche consisterait ŕ prévoir des commandes
de hausse et de tir utilisant certaines touches du clavier, qui soient distinctes pour les deux joueurs.

D) Mais le développement le plus intéressant pour notre programme serait certainement d'en
faire une application réseau. Le jeu serait alors installé sur plusieurs machines communicantes,
chaque joueur ayant le contrôle d'un seul canon. Il serait d'ailleurs encore plus attrayant de
permettre la mise en oeuvre de plus de deux canons, de maničre ŕ autoriser des combats impliquant
davantage de joueurs.
Ce type de développement suppose cependant que nous ayons appris ŕ maîtriser au préalable
deux domaines de programmation qui débordent un peu le cadre de ce cours :
- la technique des sockets, qui permet d'établir une communication entre deux ordinateurs ;
- la technique des threads, qui permet ŕ un męme programme d'effectuer plusieurs tâches simultanément (cela nous sera nécessaire, si nous voulons construire une application capable de communiquer en męme temps avec plusieurs partenaires).
Ces matičres ne font pas strictement partie des objectifs que nous nous sommes fixés pour ce
cours, et leur leur traitement nécessite ŕ lui seul un chapitre entier. Nous n'aborderons donc pas
cette question ici. Que ceux que le sujet intéresse se rassurent cependant : ce chapitre existe, mais
sous la forme d'un complément ŕ la fin du livre (chapitre 18) : vous y trouverez la version réseau de
notre jeu de bombardes.
En attendant, voyons tout de męme comment nous pouvons encore progresser, en apportant ŕ
notre projet quelques améliorations qui en feront un jeu pour 4 joueurs. Nous nous efforcerons aussi
de mettre en place une programmation bien compartimentée, de maničre ŕ ce que les méthodes de
nos classes soient réutilisables dans une large mesure. Nous allons voir au passage comment cette
évolution peut se faire sans modifier le code existant, en utilisant l'héritage pour produire de
nouvelles classes ŕ partir de celles qui sont déjŕ écrites.
Commençons par sauvegarder notre ouvrage précédent dans un fichier, dont nous admettrons
pour la suite de ce texte que le nom est : canon03.py.
Nous disposons ainsi d'un module Python, que nous pouvons importer dans un nouveau script ŕ
l'aide d'une seule ligne d'instruction. En exploitant cette technique, nous continuons ŕ perfectionner
notre application, en ne conservant sous les yeux que les nouveautés :
1. from Tkinter import *
2. from math import sin, cos, pi
3. from random import randrange
4. import canon03
5.
6. class Canon(canon03.Canon):
7. """Canon amélioré"""
8. def __init__(self, boss, id, x, y, sens, coul):
9. canon03.Canon.__init__(self, boss, id, x, y, sens, coul)
10.
11. def deplacer(self, x, y, rel =False):
12. "déplacement, relatif si <rel> est vrai, absolu si <rel> est faux"
13. if rel:
14. dx, dy = x, y
15. else:
16. dx, dy = x -self.x1, y -self.y1
17. # limites horizontales :
18. if self.sens ==1:
19. xa, xb = 20, int(self.xMax *.33)
20. else:
21. xa, xb = int(self.xMax *.66), self.xMax -20
22. # ne déplacer que dans ces limites :
23. if self.x1 +dx < xa:
24. dx = xa -self.x1
25. elif self.x1 +dx > xb:
26. dx = xb -self.x1
27. # limites verticales :
28. ya, yb = int(self.yMax *.4), self.yMax -20
29. # ne déplacer que dans ces limites :
30. if self.y1 +dy < ya:
31. dy = ya -self.y1
32. elif self.y1 +dy > yb:
33. dy = yb -self.y1
34. # déplacement de la buse et du corps du canon :
35. self.boss.move(self.buse, dx, dy)
36. self.boss.move(self.corps, dx, dy)
37. # renvoyer les nouvelles coord. au programme appelant :
38. self.x1 += dx
39. self.y1 += dy
40. self.x2 += dx
41. self.y2 += dy
42. return self.x1, self.y1
43.
44. def fin_animation(self):
45. "actions ŕ accomplir lorsque l'obus a terminé sa trajectoire"
46. # déplacer le canon qui vient de tirer :
47. self.appli.depl_aleat_canon(self.id)
48. # cacher l'obus (en l'expédiant hors du canevas) :
49. self.boss.coords(self.obus, -10, -10, -10, -10)
50.
51. def effacer(self):
52. "faire disparaître le canon du canevas"
53. self.boss.delete(self.buse)
54. self.boss.delete(self.corps)
55. self.boss.delete(self.obus)
56.
57. class AppBombardes(Frame):
58. '''Fenętre principale de l'application'''
59. def __init__(self, larg_c, haut_c):
60. Frame.__init__(self)
61. self.pack()
62. self.xm, self.ym = larg_c, haut_c
63. self.jeu = Canvas(self, width =self.xm, height =self.ym,
64. bg ='ivory', bd =3, relief =SUNKEN)
65. self.jeu.pack(padx =4, pady =4, side =TOP)
66.
67. self.guns ={} # dictionnaire des canons présents
68. self.pupi ={} # dictionnaire des pupitres présents
69. self.specificites() # objets différents dans classes dérivées
70.
71. def specificites(self):
72. "instanciation des canons et des pupitres de pointage"
73. self.master.title('<<< Jeu des bombardes >>>')
74. id_list =[("Paul","red"),("Roméo","cyan"),
75. ("Virginie","orange"),("Juliette","blue")]
76. s = False
77. for id, coul in id_list:
78. if s:
79. sens =1
80. else:
81. sens =-1
82. x, y = self.coord_aleat(sens)
83. self.guns[id] = Canon(self.jeu, id, x, y, sens, coul)
84. self.pupi[id] = canon03.Pupitre(self, self.guns[id])
85. s = not s # changer de côté ŕ chaque itération
86.
87. def depl_aleat_canon(self, id):
88. "déplacer aléatoirement le canon <id>"
89. gun =self.guns[id]
90. dx, dy = randrange(-60, 61), randrange(-60, 61)
91. # déplacement (avec récupération des nouvelles coordonnées) :
92. x, y = gun.deplacer(dx, dy, True)
93. return x, y
94.
95. def coord_aleat(self, s):
96. "coordonnées aléatoires, ŕ gauche (s =1) ou ŕ droite (s =-1)"
97. y =randrange(int(self.ym /2), self.ym -20)
98. if s == -1:
99. x =randrange(int(self.xm *.7), self.xm -20)
100. else:
101. x =randrange(20, int(self.xm *.3))
102. return x, y
103.
104. def goal(self, i, j):
105. "le canon n°i signale qu'il a atteint l'adversaire n°j"
106. # de quel camp font-ils partie chacun ?
107. ti, tj = self.guns[i].sens, self.guns[j].sens
108. if ti != tj : # ils sont de sens opposés :
109. p = 1 # on gagne 1 point
110. else: # ils sont dans le męme sens :
111. p = -2 # on a touché un allié !!
112. self.pupi[i].attribuerPoint(p)
113. # celui qui est touché perd de toute façon un point :
114. self.pupi[j].attribuerPoint(-1)
115.
116. def dictionnaireCanons(self):
117. "renvoyer le dictionnaire décrivant les canons présents"
118. return self.guns
119.
120.if __name__ =='__main__':
121. AppBombardes(650,300).mainloop()
Commentaires :
- Ligne 6 : La forme d'importation utilisée ŕ la ligne 4 nous permet de redéfinir une nouvelle
classe Canon() dérivée de la précédente, tout en lui conservant le męme nom. De cette maničre,
les portions de code qui utilisent cette classe ne devront pas ętre modifiées (Cela n'aurait pas été
possible si nous avions utilisé par exemple : « from canon03 import * »).
- Lignes 11 ŕ 16 : La méthode définie ici porte le męme nom qu'une méthode de la classe parente.
Elle va donc remplacer celle-ci dans la nouvelle classe (On pourra dire également que la
méthode deplacer() a été surchargée). Lorsque l'on réalise ce genre de modification, on
s'efforce en général de faire en sorte que la nouvelle méthode effectue le męme travail que
l'ancienne quand elle est invoquée de la męme façon que l'était cette derničre. On s'assure ainsi
que les applications qui utilisaient la classe parente pourront aussi utiliser la classe fille, sans
devoir ętre elles-męmes modifiées.
Nous obtenons ce résultat en ajoutant un ou plusieurs paramčtres, dont les valeurs par défaut forceront l'ancien comportement. Ainsi, lorsque l'on ne fournit aucun argument pour le paramčtre rel, les paramčtres x et y sont utilisés comme des coordonnées absolues (ancien comportement de la méthode). Par contre, si l'on fournit pour rel un argument « vrai », alors les paramčtres x et y sont traités comme des déplacements relatifs (nouveau comportement). - Lignes 17 ŕ 33 : Les déplacements demandés seront produits aléatoirement. Il nous faut donc
prévoir un systčme de barričres logicielles, afin d'éviter que l'objet ainsi déplacé ne sorte du
canevas.
- Ligne 42 : Nous renvoyons les coordonnées résultantes au programme appelant. Il se peut en
effet que celui-ci commande un déplacement du canon sans connaître sa position initiale.
- Lignes 44 ŕ 49 : Il s'agit encore une fois de surcharger une méthode qui existait dans la classe
parente, de maničre ŕ obtenir un comportement différent : aprčs chaque tir, désormais on ne
disperse plus tous les canons présents, mais seulement celui qui vient de tirer.
- Lignes 51 ŕ 55 : Méthode ajoutée en prévision d'applications qui souhaiteraient installer ou
retirer des canons au fil du déroulement du jeu.
- Lignes 57 et suivantes : Cette nouvelle classe est conçue dčs le départ de maničre telle qu'elle puisse aisément ętre dérivée. C'est la raison pour laquelle nous avons fragmenté son constructeur en deux parties : La méthode __init__() contient le code commun ŕ tous les objets, aussi bien ceux qui seront instanciés ŕ partir de cette classe que ceux qui seront instanciés ŕ partir d'une classe dérivée éventuelle. La méthode specificites() contient des portions de code plus spécifiques : cette méthode est clairement destinée ŕ ętre surchargée dans les classes dérivées éventuelles.
15.2. Jeu de Ping▲
Dans les pages qui suivent, vous trouverez le script correspondant ŕ un petit programme complet. Ce programme vous est fourni ŕ titre d'exemple de ce que vous pouvez envisager de développer vous-męme comme projet personnel de synthčse. Il vous montre encore une fois comment vous pouvez utiliser plusieurs classes afin de construire un script bien structuré.
15.2.1. Principe▲
Le «jeu» mis en oeuvre ici est plutôt une sorte d'exercice mathématique. Il se joue sur un panneau
ou est représenté un quadrillage de dimensions variables, dont toutes les cases sont occupées par
des pions. Ces pions possčdent chacun une face blanche et une face noire (comme les pions du jeu
Othello/Reversi), et au début de l'exercice ils présentent tous leur face blanche par-dessus.
Lorsque l'on clique sur un pion ŕ l'aide de la souris, les 8 pions adjacents se retournent.
Le jeu consiste alors ŕ essayer de retourner tous les pions, en cliquant sur certains d'entre eux.
L'exercice est trčs facile avec une grille de 2 x 2 cases (il suffit de cliquer sur chacun des 4
pions). Il devient plus difficile avec des grilles plus grandes, et est męme tout ŕ fait impossible avec
certaines d'entre elles. A vous de déterminer lesquelles !
(Ne négligez pas d'étudier le cas des grilles 1 x n).

Note : Vous trouverez la discussion complčte du jeu de Ping, sa théorie et ses extensions, dans la revue « Pour la science » n° 298 - Aoűt 2002, pages 98 ŕ 102.
15.2.2. Programmation▲
Lorsque vous développez un projet logiciel, veillez toujours ŕ faire l'effort de décrire votre
démarche le plus clairement possible. Commencez par établir un cahier des charges détaillé, et ne
négligez pas de commenter ensuite trčs soigneusement votre code, au fur et ŕ mesure de son
élaboration (et non aprčs coup !).
En procédant ainsi, vous vous forcez vous-męme ŕ exprimer ce que vous souhaitez que la
machine fasse, ce qui vous aide ŕ analyser les problčmes et ŕ structurer convenablement votre code.
Cahier des charges du logiciel ŕ développer
L'application sera construite sur la base d'une fenętre principale comportant le panneau de jeu et une barre de menus.
-
L'ensemble devra ętre extensible ŕ volonté par l'utilisateur, les cases du panneau devant cependant rester carrées.
-
Les options du menu permettront de :
-
choisir les dimensions de la grille (en nombre de cases)
-
réinitialiser le jeu (c'est-ŕ-dire disposer tous les pions avec leur face blanche au-dessus)
-
afficher le principe du jeu dans une fenętre d'aide
-
terminer.(fermer l'application)
-
-
La programmation fera appel ŕ trois classes :
-
une classe principale
-
une classe pour la barre de menus
-
une classe pour le panneau de jeu
-
Le panneau de jeu sera dessiné dans un canevas, lui-męme installé dans un cadre (frame). En fonction des redimensionnements opérés par l'utilisateur, le cadre occupera ŕ chaque fois toute la place disponible : il se présente donc au programmeur comme un rectangle quelconque, dont les dimensions doivent servir de base au calcul des dimensions de la grille ŕ dessiner.
-
Puisque les cases de cette grille doivent rester carrées, il est facile de commencer par calculer leur taille maximale, puis d'établir les dimensions du canevas en fonction de celle-ci.
-
Gestion du clic de souris : on liera au canevas une méthode-gestionnaire pour l'événement <clic du bouton gauche>. Les coordonnées de l'événement serviront ŕ déterminer dans quelle case de la grille (n° de ligne et n° de colonne) le clic a été effectué, quelles que soient les dimensions de cette grille. Dans les 8 cases adjacentes, les pions présents seront alors « retournés » (échange des couleurs noire et blanche).
###########################################
# Jeu de ping #
# Références : Voir article de la revue #
# <Pour la science>, Aout 2002 #
# #
# (C) Gérard Swinnen (Verviers, Belgique) #
# http://www.ulg.ac.be/cifen/inforef/swi #
# #
# Version du 29/09/2002 - Licence : GPL #
###########################################
from Tkinter import *
class MenuBar(Frame):
"""Barre de menus déroulants"""
def __init__(self, boss =None):
Frame.__init__(self, borderwidth =2, relief =GROOVE)
##### Menu <Fichier> #####
fileMenu = Menubutton(self, text ='Fichier')
fileMenu.pack(side =LEFT, padx =5)
me1 = Menu(fileMenu)
me1.add_command(label ='Options', underline =0,
command = boss.options)
me1.add_command(label ='Restart', underline =0,
command = boss.reset)
me1.add_command(label ='Terminer', underline =0,
command = boss.quit)
fileMenu.configure(menu = me1)
##### Menu <Aide> #####
helpMenu = Menubutton(self, text ='Aide')
helpMenu.pack(side =LEFT, padx =5)
me1 = Menu(helpMenu)
me1.add_command(label ='Principe du jeu', underline =0,
command = boss.principe)
me1.add_command(label ='A propos ...', underline =0,
command = boss.aPropos)
helpMenu.configure(menu = me1)
class Panneau(Frame):
"""Panneau de jeu (grille de n x m cases)"""
def __init__(self, boss =None):
# Ce panneau de jeu est constitué d'un cadre redimensionnable
# contenant lui-męme un canevas. A chaque redimensionnement du
# cadre, on calcule la plus grande taille possible pour les
# cases (carrées) de la grille, et on adapte les dimensions du
# canevas en conséquence.
Frame.__init__(self)
self.nlig, self.ncol = 4, 4 # Grille initiale = 4 x 4
# Liaison de l'événement <resize> ŕ un gestionnaire approprié :
self.bind("<Configure>", self.redim)
# Canevas :
self.can =Canvas(self, bg ="dark olive green", borderwidth =0,
highlightthickness =1, highlightbackground ="white")
# Liaison de l'événement <clic de souris> ŕ son gestionnaire :
self.can.bind("<Button-1>", self.clic)
self.can.pack()
self.initJeu()
def initJeu(self):
"Initialisation de la liste mémorisant l'état du jeu"
self.etat =[] # construction d'une liste de listes
for i in range(12): # (équivalente ŕ un tableau
self.etat.append([0]*12) # de 12 lignes x 12 colonnes)
def redim(self, event):
"Opérations effectuées ŕ chaque redimensionnement"
# Les propriétés associées ŕ l'événement de reconfiguration
# contiennent les nouvelles dimensions du cadre :
self.width, self.height = event.width -4, event.height -4
# La différence de 4 pixels sert ŕ compenser l'épaisseur
# de la 'highlightbordure" entourant le canevas)
self.traceGrille()
def traceGrille(self):
"Dessin de la grille, en fonction des options & dimensions"
# largeur et hauteur maximales possibles pour les cases :
lmax = self.width/self.ncol
hmax = self.height/self.nlig
# Le coté d'une case sera égal ŕ la plus petite de ces dimensions :
self.cote = min(lmax, hmax)
# -> établissement de nouvelles dimensions pour le canevas :
larg, haut = self.cote*self.ncol, self.cote*self.nlig
self.can.configure(width =larg, height =haut)
# Tracé de la grille :
self.can.delete(ALL) # Effacement dessins antérieurs
s =self.cote
for l in range(self.nlig -1): # lignes horizontales
self.can.create_line(0, s, larg, s, fill="white")
s +=self.cote
s =self.cote
for c in range(self.ncol -1): # lignes verticales
self.can.create_line(s, 0, s, haut, fill ="white")
s +=self.cote
# Tracé de tous les pions, blancs ou noirs suivant l'état du jeu :
for l in range(self.nlig):
for c in range(self.ncol):
x1 = c *self.cote +5 # taille des pions =
x2 = (c +1)*self.cote -5 # taille de la case -10
y1 = l *self.cote +5 #
y2 = (l +1)*self.cote -5
coul =["white","black"][self.etat[l][c]]
self.can.create_oval(x1, y1, x2, y2, outline ="grey",
width =1, fill =coul)
def clic(self, event):
"Gestion du clic de souris : retournement des pions"
# On commence par déterminer la ligne et la colonne :
lig, col = event.y/self.cote, event.x/self.cote
# On traite ensuite les 8 cases adjacentes :
for l in range(lig -1, lig+2):
if l <0 or l >= self.nlig:
continue
for c in range(col -1, col +2):
if c <0 or c >= self.ncol:
continue
if l ==lig and c ==col:
continue
# Retournement du pion par inversion logique :
self.etat[l][c] = not (self.etat[l][c])
self.traceGrille()
class Ping(Frame):
"""corps principal du programme"""
def __init__(self):
Frame.__init__(self)
self.master.geometry("400x300")
self.master.title(" Jeu de Ping")
self.mbar = MenuBar(self)
self.mbar.pack(side =TOP, expand =NO, fill =X)
self.jeu =Panneau(self)
self.jeu.pack(expand =YES, fill=BOTH, padx =8, pady =8)
self.pack()
def options(self):
"Choix du nombre de lignes et de colonnes pour la grille"
opt =Toplevel(self)
curL =Scale(opt, length =200, label ="Nombre de lignes :",
orient =HORIZONTAL,
from_ =1, to =12, command =self.majLignes)
curL.set(self.jeu.nlig) # position initiale du curseur
curL.pack()
curH =Scale(opt, length =200, label ="Nombre de colonnes :",
orient =HORIZONTAL,
from_ =1, to =12, command =self.majColonnes)
curH.set(self.jeu.ncol)
curH.pack()
def majColonnes(self, n):
self.jeu.ncol = int(n)
self.jeu.traceGrille()
def majLignes(self, n):
self.jeu.nlig = int(n)
self.jeu.traceGrille()
def reset(self):
self.jeu.initJeu()
self.jeu.traceGrille()
def principe(self):
"Fenętre-message contenant la description sommaire du principe du jeu"
msg =Toplevel(self)
Message(msg, bg ="navy", fg ="ivory", width =400,
font ="Helvetica 10 bold",
text ="Les pions de ce jeu possčdent chacun une face blanche et "\
"une face noire. Lorsque l'on clique sur un pion, les 8 "\
"pions adjacents se retournent.\nLe jeu consiste a essayer "\
"de les retouner tous.\n\nSi l'exercice se révčle trčs facile "\
"avec une grille de 2 x 2 cases. Il devient plus difficile avec "\
"des grilles plus grandes. Il est męme tout ŕ fait impossible "\
"avec certaines grilles.\nA vous de déterminer lesquelles !\n\n"\
"Réf : revue 'Pour la Science' - Aout 2002")\
.pack(padx =10, pady =10)
def aPropos(self):
"Fenętre-message indiquant l'auteur et le type de licence"
msg =Toplevel(self)
Message(msg, width =200, aspect =100, justify =CENTER,
text ="Jeu de Ping\n\n(C) Gérard Swinnen, Aout 2002.\n"\
"Licence = GPL").pack(padx =10, pady =10)
if __name__ == '__main__':
Ping().mainloop()
Rappel : Si vous souhaitez expérimenter ces programmes sans avoir ŕ les réécrire, vous pouvez trouver leur code source ŕ l'adresse : http://www.ulg.ac.be/cifen/inforef/swi/python.htm



